“如何突破解析几何中的难点”从一道试题分析

□崔星邦

(审稿:伊翠红)

(本文责编:赵宁宁)

解析几何题的难点主要在于:题目条件的翻译和计算量,下面以一道试题为例,分析如何突破解析几何的难点。

一、第(1)问分析

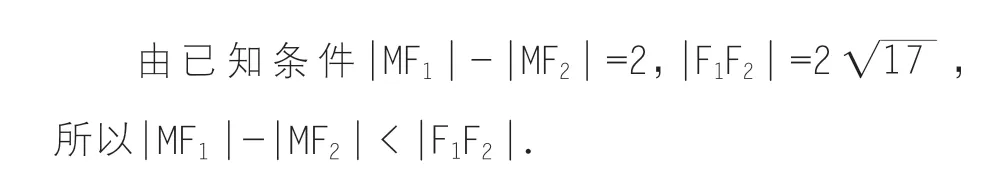
根据双曲线的定义知,点M 的轨迹C 是以F1、F2为焦点,实轴长为2 的双曲线的右支.

所以M 的轨迹方程为:x2-=1（x≥1）.

第（1）问要注意题目条件的翻译,要会用圆锥曲线的定义分析出点M 的轨迹为双曲线的一支,如果直接翻译题目条件,化简方程迈算量大,甚至影响第（2）问的解答。

二、第(2)问分析

(一)直译条件一一一按所需耐心算

解法1：基本方法一一一直接翻译条件，耐心进行运算

(这样将题目条件翻译成我们熟悉的形式,下面联立方程借助韦达定理计算x1x2和x1+x2)

整理可得k12=k22,又因为k1≠k2,所以k1+k2=0.

因此,直线AB 与直线PQ 的斜率之和为0.

2.3 超声微泡造影剂携RPM对PCNA的mRNA及蛋白表达影响 PCNA 的mRNA 表达产物校正后分析，对照组、RPM组和超声微泡造影剂携RPM组统计结果用±s表示：分别为219.31±7.21，147.32±10.27和97.17±8.79，两两比较RPM组和超声微泡造影剂携RPM组两组与对照组之间存在显著差异(P<0.05)，同时超声微泡造影剂携RPM组也明显低于RPM组。使用Westernblot检测T24 细胞PCNA蛋白的表达量，结果表明在RPM和超声微泡造影剂携RPM作用细胞24 h后，两组细胞的PCNA蛋白的表达量明显下降(图2)。

解法1 的思路非常简单,属于直接翻译条件来求解,但是计算量偏大。那么我们思考:是否有方法对迈算进行优化？

解法2：对解法1 的运算进行优化

(二)条件翻译一一一多角度思考

通过观察我们发现T、A、B 三点共线,T、P、Q 三点共线。因此,可以从下面两个知识点来考虑,一是把“距离乘积”转化为“向量”来处理,二是从直线的方程入手,有一种形式的直线方程与向量有紧密的联系,即直线的参数方程,它由一个定点和这条直线的方向向量唯一确定。

解法3：用向量转化距离乘积

解法4：直线方程的参数方程形式

其中,t 为参数,α 为直线AB 的倾斜角,β 为直线PQ 的倾斜角,且α≠β.

解法4 用到设方程的另一种形式——直线的参数方程,利用参数方程中参数的几何意义使题目的迈算得到简化,新教材选择性必修第一册的探究与发现中提到了参数方程,同学们可以学习一下,方便对解析几何题的简化迈算。

(三)必要性探路一一一由特殊到一般

这道解析几何题本质上是定值问题,对于定值定点问题,我们可以采用先猜再证的方法,由特殊到一般得到结论。

解法5：必要性探路

解法5 应用必要性探路的方法先把结论得到,然后再证明一般性也成立,与解法1 相比简化了的迈算过程,使同学们放平了心态。

(四)几何问题一一一平面几何来辅助

我们回归本质看问题,解析几何问题归根结底也是几何问题,我们通过图象从几何上分析一下问题,翻译题目条件。

解法6：借助平面几何解决问题

由题意,我们画出草图:

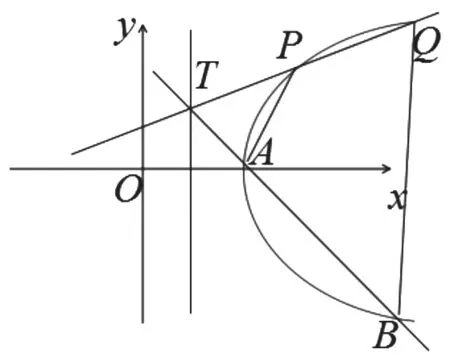
又因为∠ATP=∠QTB,所以△ATP～△QTB,

所以∠TAP=∠TQB,所以∠BAP+∠TQB=180o,

所以A,B,Q,P 四点共圆.

因为A,B,Q,P 四点共圆,所以k1+k2=0.

解法6 从平面几何出发看本质,发现四点共圆,从而简化计算。其实这个题的几何原型应该为圆幂定理,这一几何原型在高中解析几何题中的应用也是比较广泛的。

我们以此题为载体总结一下如何突破解析几何的难点:首先,多数同学看到解析几何题都会直接翻译条件,但计算复杂,这时应先观察式子结构优化计算,如采用整体思想、换元法等；其次,多角度思考问题,从不同角度翻译题目条件,比如本题的距离可以翻译为向量,还有直线方程的表示方法也多种多样,合当选择直线方程的表示形式也可以优化计算,如可以利用参数方程的几何意义使迈算变简单；再次,对于定值定点类问题,可以由特殊到一般,先得出结论再证明；最后,还要充分挖掘题目的几何本质,数形结合,先从几何方面优化题目代数条件,再用代数方法解决几何问题。