G-布朗驱动下的非线性中立型随机延迟微分方程解的存在唯一性研究

张可为，袁海燕

(黑龙江工程学院 理学院，哈尔滨 150050)

中立型随机延迟微分方程被广泛地应用于经济、金融、生物、医学、物理等科学领域的模型建立，因其在理论和实践中具有重要意义，引起了越来越多学者的关注，例如文献[1-4]研究了中立型随机微分方程模型在传染病和族群动态中的应用，文献[5-6]研究了中立型随机微分方程模型在金融、物理和工程模型中的应用。

非线性期望理论,特别是彭实戈[7]提出的次线性期望G-期望，由于其在不确定性问题、风险度量、金融飞速发展等方面的潜在应用，引起了研究者的极大兴趣。彭实戈在文献[7]中建立了时间相容的G-期望和G-条件期望的基本理论，其中，G是非线性热方程的无穷小生成元。基于G-期望的框架，在文献[8]引入G-高斯分布和G-布朗运动，并利用它们建立相应的积分。另外，胡明上和彭实戈文献[8]中提到存在一个弱紧的概率测度族，它可以用来表示重要的次线性期望G-期望，从而定义了相关的容量。自此，关于G-布朗运动的随机微分方程的研究逐渐展开。由于随机微分方程解析解显示表达式很难获得，解的存在唯一性及数值方法的相关研究显得尤为重要。关于随机泛函微分方程解的存在唯一性研究结论可以参阅文献[9-12]。关于G-布朗运动驱动的非线性中立型随机延迟微分方程解的存在性及数值研究目前还没有找到相应文献，文中将给出G-布朗运动驱动的非线性中立型随机延迟微分方程解的存在性及唯一性分析。

1 预备知识

文中研究如下形式的非线性中立型随机延迟微分方程

d[y(t)-Ny(t-τ)]=f(t,y(t),y(t-τ))dt+

g(t,y(t),y(t-τ)dωt+h(t,y(t),

y(t-τ))d〈ω〉t,t∈[0,T].

(1)

满足下列初始条件

y0=ξ={φ(θ),θ∈[-τ,0]}.

(2)

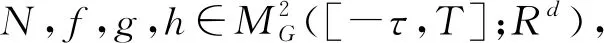
满足初始条件(2)的中立型随机延迟微分方程(1)可以等价为下面的积分微分方程

y(t)-Ny(t-τ)=ξ(0)-N(ξ(0-τ))+

(3)

为了研究解的存在唯一性，假设函数f,g和h满足下列条件：

(H1) Lipschitz条件。存在正常数L，使得不等式

|f(t,x1,y1)-f(t,x2,y2)|2∨|g(t,x1,y1)-

g(t,x2,y2)|2∨|h(t,x1,y1)-h(t,x2,y2)|2≤

L(|x1-x2|2+|y1-y2|2)

(4)

对所有的x1,y1,x2,y2∈Rd及t≥0成立。

由式(4)可以得到线性增长条件。

(H2)线性增长条件。存在常数G1>0，使得不等式

|f(t,x,y)|∨|g(t,x,y)|∨|h(t,x,y)|≤

G1(1+|x|2+|y|2)

(5)

对于所有的(t,x,y)∈R+×Rd×Rd都成立。

(H3)存在常数κ∈(0,1)，使得对于所有x,y∈Rd及t≥0，下面不等式成立

|N(x)-N(y)|≤κ|x-y|.

(6)

另外，假设t≥0时，N(t,0)=0，由式(6)得N(x)≤κ|x|。

2 解的存在唯一性

本部分给出非线性中立型随机延迟微分方程解的存在唯一性结论及证明。

定理1 假设f,g及h满足Lipschitz条件，且存在非负常数λ>0使得不等式

〈z,f(t,z,0)〉≤-λ|z|2

(7)

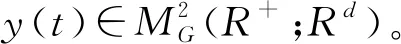
(8)

证明分为三步给出定理的证明。

1)有界性。

对于T>0及整数n≥1，定义截断时间

τn=T∧inf{t∈[0,T]∶|y(t)|≥n}.

显然，τn↑Ta.s.记yn(t)=y(t∧τn),t∈[0,T]，则yn(t)满足方程

yn(t)-N(yn(t-τ))=ξ(0)-N(ξ(-τ))+

(9)

令

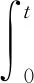
应用Yang不等式及Hölder不等式，有

(10)

两侧同时取G-期望，得到

(11)

由于

所以有

(12)

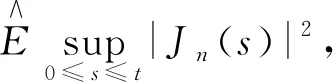
yn(s-τ))I[[0,τn]](s)d〈ω〉(s)|2.

(13)

结合Hölder不等式和线性增长条件，可以得到

(14)

由文献[8]中的推论8及Doob鞅不等式，可以得到

(15)

同样，可以得到

(16)

将式(14)—(16)代入式(13)，得到

代入式(12)可得

(17)

由Gronwall不等式，得

令n→∞可得式(8)。

2)唯一性。

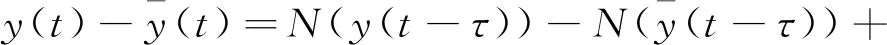
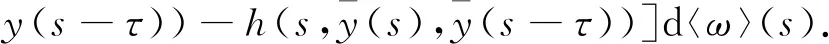
(18)

类似于有界性的证明，有

应用Gronwall不等式，得到

3)存在性。

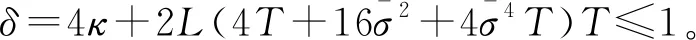
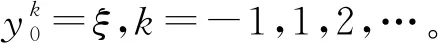
yn(t)=ξ+N(yn-1(t-τ))-N(ξ(-τ))+

(19)

|yn(t)|2≤5E|ξ|2+5|N(yn-1(t-τ))-

(20)

两侧同时取G-期望，由式(11)、文献[8]中的推论8及Doob鞅不等式(取p=2)可得

(21)

应用线性增长条件，可以得到

G1|yn-1(s)|2+G1|yn-1(s-τ)|2)ds+

(22)

其中

因此，对于任意k≥1，可以推得

注意到

可以得到

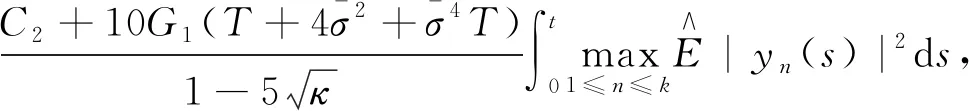
(23)

由k的任意性，可以得到对所有0≤t≤T,n≥1。

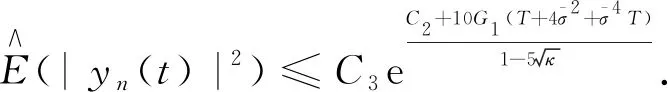
(24)

由初等不等式，可以得

|y1(t)-y0(t)|2=|y1(t)-y0|2≤

4|N(y0(t-τ))-N(y-1(-τ))|2+

y0(s-τ))d〈ω〉(s)|2.

(25)

式(25)两侧同时取G-期望，由式(11)、文献[8]中的推论8及G-It积分性质，可得

(26)

即

取t=T，则有

对于n≥0及0≤t≤T，有不等式

|yn+1(t)-yn(t)|2≤4|N(yn(t-τ))-

yn(s-τ))-f(s,yn-1(s),yn-1(s-τ))]ds|2+

yn(s-τ))-h(s,yn-1(s),yn-1(s-τ))]d〈ω〉(s)|2.

(27)

应用Lipschitz条件(4)及不等式(6)可以得到

yn(s-τ))-h(s,yn-1(s),yn-1(s-τ))|2ds≤

(28)

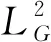
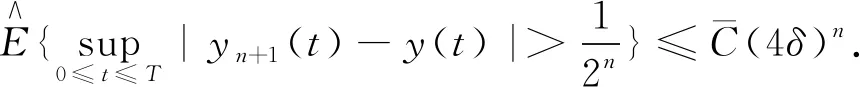
令式(24)中n→∞，则有

对所有的0≤t≤T成立。因此,有y(·)∈M2([0,T];Rd)。

下面证明y(t)满足方程(1)。

yn(s-τ))-f(s,y(s),y(s-τ))|2ds+

yn(s-τ))-h(s,y(s),y(s-τ))|2ds≤2L[(1+

(29)

y(s),y(s-τ))d〈ω〉(s)|2≤2L[(1+

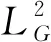
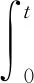
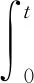
对于0≤t≤T，对式(19)两侧取极限，可得

即

y(t)-N(y(t-τ))=ξ(0)-N(ξ(-τ))+

0≤t≤T.

以上证明了y(t)是方程(1)的解。定理证毕。