小型悬索并联机器人的系统设计

辛玉红,王翠红,杨庆凤

(金陵科技学院机电工程学院,江苏 南京 211169)

悬索机器人利用悬索代替传统机器人中的刚性连杆作为驱动元件,在期望的工作空间中对末端执行器进行定位和定向,具有并联、柔性驱动的特点,且易拆易构、工作空间大、移动速度快、惯性小、质量承载比高[1-3],因而在大型工作空间如场地摄影[4]、智能物流仓储[5]、大型3D打印[6]等有着巨大的应用前景。

悬索机器人工作时末端执行器与外界环境发生接触,产生作用力，这时如果仅使用传统的位置控制策略[7],则控制精度无法保障。力位混合控制作为主动柔顺控制的一种,其核心控制策略是实现对机器人末端力与位置的综合控制,进而提高机器人的控制精度及稳定性[8]，已逐渐被应用于悬索机器人控制中。Jun等[9]在位置环和力环使用两个矩阵计算绕线误差,构建三自由度悬索机器人力位混合控制系统。Kraus等[10]使用位置、绳索内力、外界接触力三环控制策略,使绳索保持张紧并按设定轨迹运动。尤开灵[11]基于悬索机械臂的导纳柔顺控制算法设计了一种位姿预测的力位混合控制方案。

这些悬索机器人力位混合控制系统一般需要较高的硬件性能、昂贵的力传感器,使其推广应用受到了制约。本文采用电机内部的力矩传感器代替力传感器,设计了一种无外力传感器、计算效率高的力位混合控制系统,保障机器人的稳定性及运动控制精度。

1 悬索机器人模型

1.1 样机模型

图1 悬索机器人样机

平面四悬索机器人(图1)主要由静平台、动平台、柔索等组成。静平台固定于基座上,装有驱动电机,用以收放绳索;动平台为控制终端,可依据工作需要搭载不同的末端执行器,例如摄像机、机械手等;利用柔索将动平台与出绳点连接,通过电机收放绳索以控制动平台的精准运动。因机器人动力部分与运动控制部分相分离,故质量承载比比串联机器人更高,末端执行器惯性更小,运动速度更快。

该机器人各部分参数及功能如表1所示。

表1 悬索机器人各部分参数及功能

1.2 收放绳装置

收放绳装置是悬索机器人的核心部件,多个收放绳装置协同工作，控制悬索长度,实现对悬索机器人末端平台的定位控制。收放绳装置的精度决定了悬索机器人的运动性能。本文针对小型悬索机器人设计了一种精准收放绳装置,如图2所示。

具体工作原理为:丝杆固连不动,与绕线轮通过丝杆螺母连接。左右法兰间固定三根长导杆,绕线轮可沿导杆滑动。绕线轮外表面加工有与丝杆相同螺距的螺纹。电机通过电机输出轴带动其固接的法兰转动,从而带动导杆、绕线轮一起转动,在固定丝杆的作用下,绕线轮每转动一周的同时沿导杆平动一个螺距长度,使柔索缠绕在绕线轮的凹槽内。该装置保证绕线不重叠及绕线轮出绳点固定,避免因绕线不均产生机械误差,实现了机器人在悬索收放过程中的绳长精准控制,保证了末端执行装置的位置精度。

1.3 驱动系统

本文选用的SM30伺服电机最大输出力矩为3 N·m,多圈绝对位置可控,控制精度可达0.088°,内部装有多种传感器,能反馈温度、速度、位置、负载、电流等多项物理参数。其部分参数如表2所示。

表2 伺服电机部分参数

1.4 控制系统

悬索机器人样机选用Arduino Mega 2560作为控制板。控制板与电机采用串口通信,指定电机目标位置,带动收放绳装置转动。

2 运动学和静力学分析

2.1 运动学分析

建立如图3所示的机器人模型,图中O-xyz为世界坐标系,D-xyz为动平台局部坐标系,Ai(i=1～4)为静平台绳索出绳点,Bi(i=1～4)为动平台绳索铰接点,ai、b分别为静平台出绳点Ai、动平台几何中心D在O-xyz坐标系下的位置向量,bi为Bi在D-xyz坐标系下的位置向量,li为绳索向量,Li为对应的绳索长度。

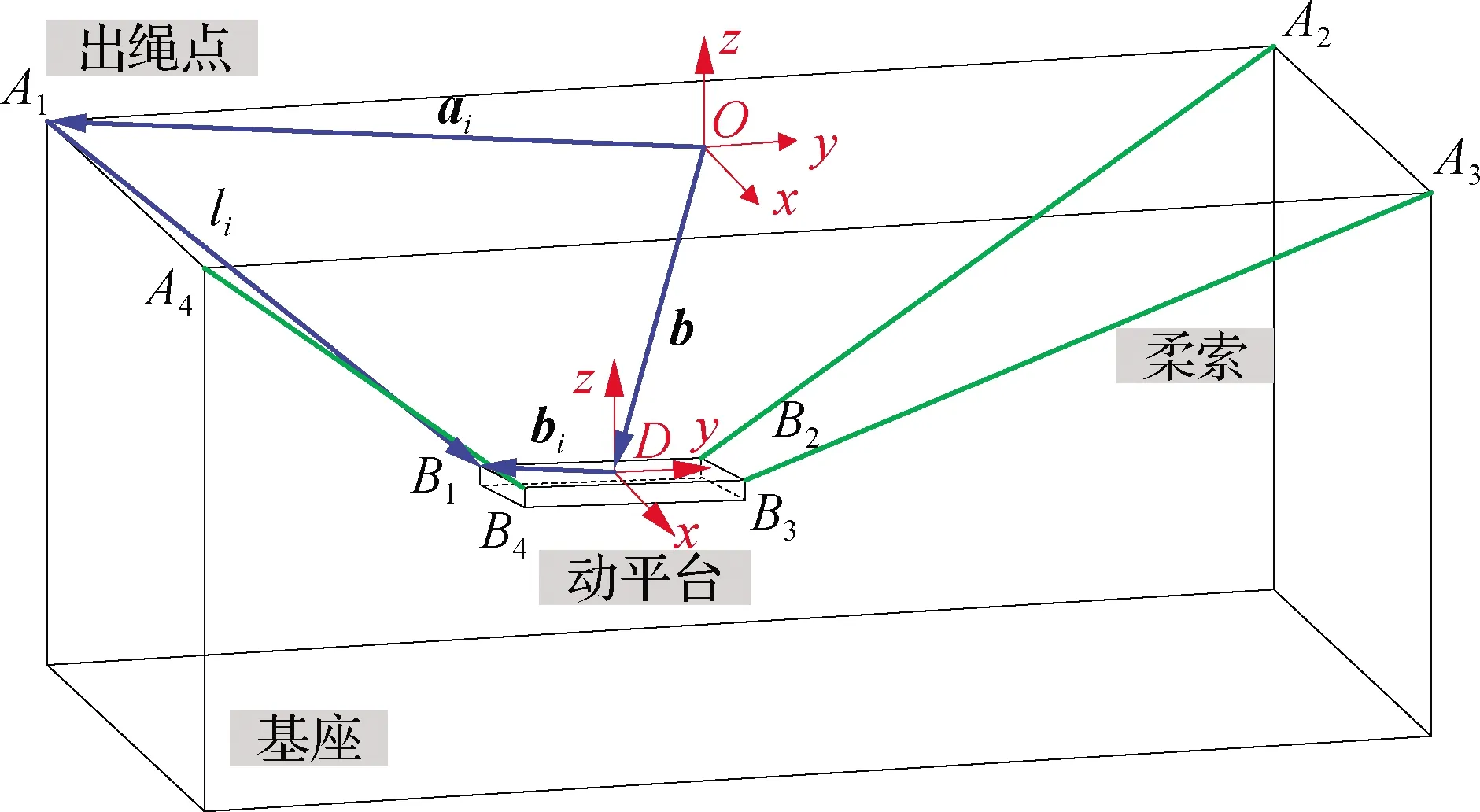
图3 小型悬索机器人模型

运动学反解是控制悬索机器人的基础,即根据动平台位姿计算各绳索长度Li。设动平台欧拉角分别为α,β,γ,记c为cos函数,s为sin函数,则动平台的旋转矩阵可表示为

(1)

(2)

2.2 静力学分析

动平台只受四根绳索的拉力Fi(i=1～4)和外力W影响,设

F=[F1,F2,F3,F4]T

(3)

动平台静止时，绳索张力对动平台产生的力、力矩与动平台所受外力W正好抵消，如式(4)：

(4)

(5)

其中，CT是机器人动平台的结构矩阵,W=[fw,τw]T,fw和τw分别表示动平台所受外力和外力矩，ti为绳索单位矢量,|Fmin|是绳索张力最小值,|Fmax|是绳索张力最大值。

3 力位混合控制系统

悬索机器人控制系统的核心是点位运动及轨迹运动算法。在传统的位置控制系统[7]中,点位控制系统单独调用各电机速度规划算法计算各电机位置;轨迹控制系统根据速度规划算法插补出末端位姿,并经运动学反解计算得到各电机位置,完成悬索机器人的运动控制。

在动平台受到接触力作用时,传统的位置控制系统无法保障机器人的控制精度,因此本文设计了一种力位混合控制系统，如图4所示。

图4 力位混合运动控制系统算法框

该控制系统中,力控环节由电机内部的力矩测量功能对悬索张力进行反馈和控制调节;位控环节对动平台末端位置进行控制,根据悬索张力传递的特性,由结构矩阵计算出动平台悬挂外力,从而确定动平台末端的位置。具体实施步骤如下:

1)力控环节。预设悬索机器人动平台所受外力及外力矩(外力悬量)Wset;将Wset输入张力优化算法模块,运用CF张力优化算法[12]计算出期望的悬索张力Fset;由电机的力矩测量功能测量出每根悬索对应电机的力矩,将其转化为实际的悬索张力Freal;将Fset与Freal作差,计算出悬索张力误差ΔF;将ΔF输入悬索张力力控算法模块,经计算可求出ΔF对应的悬索长度补偿量ΔL。

为了简化计算,本文中悬索张力力控算法为一个比例增益的控制器,设K为悬索材料刚度,则悬索刚度Kcable=L/K(L为悬索长度),ΔF与ΔL之间的关系如式(6)所示:

(6)

2) 位控环节。预设动平台运动轨迹Xset,力控环节中的Freal经过结构矩阵模块的计算(Wreal=-CTFreal)，得到实际的动平台所受外力(实际外力悬量)Wreal；将预设的外力悬量Wset与实际的外力悬量Wreal作差,计算出外力悬量误差ΔW;将ΔW输入动平台末端力控算法模块,经计算可求出ΔW对应的动平台运动轨迹补偿量ΔX;将动平台预设轨迹Xset与ΔX相加得到新的动平台运动轨迹Xnew;将Xnew输入运动学反解模块,求得悬索长度L。

3)力位混合控制。将L与ΔL相加得到这一控制周期内力位混合控制算法补偿过的悬索长度值Lnew,控制电机运动。

4 实验结果与分析

4.1 仿真实验

为了验证力位混合控制系统的有效性,在Simulink中构建仿真模型。选取矩形动平台长a为100 mm,宽b为100 mm,设置出绳点OAi及铰接点DBi坐标，如表3所示。

表3 出绳点及铰接点坐标

预设动平台运动路径为其工作空间内的整圆,其方程如下:

(7)

结合出绳点的具体位置,取R=350,x′=-125,y′=-110,s表示不同位置点对应的圆心角。计算得到不同位置柔索长度如图5所示,柔索张力如图6所示。

图5 不同位置时柔索长度情况

图6 不同位置时柔索张力情况

从图中可以看出:在移动过程中,柔索长度的数值和轨迹变化合理,过渡光滑;柔索张力均在最小张力和最大张力之间,在实际运行过程中各柔索受力平稳,较为可靠,表明算法具有可行性。在Simulink中仿真时,为尽量还原现实物理环境,在每个运动控制周期内,对悬挂外力fw产生2 N以下的随机力来代表力扰动,分别采用位置控制算法和力位混合控制算法得到轨迹误差，如表4所示。从表4可以看出,受干扰后未经力位补偿的动平台轨迹Xreal与预设的动平台轨迹Xset之间存在较大差异,此时悬索机器人的稳定性及控制精度得不到保障。经过力位混合控制算法补偿后的Xnew与Xset之间的差异很小,精度可以达到10-2cm数量级。

表4 力位控制补偿前后轨迹误差对比

4.2 样机实验

为验证定位控制的精确性,在动平台上垂直安装马克笔,通过对末端动平台轨迹进行控制,在纸面上得到预定的运动轨迹；通过测量曲线的偏移程度,得出动平台的控制精度。在AutoCAD中设计动平台末端轨迹曲线及其部分坐标，如图7所示。

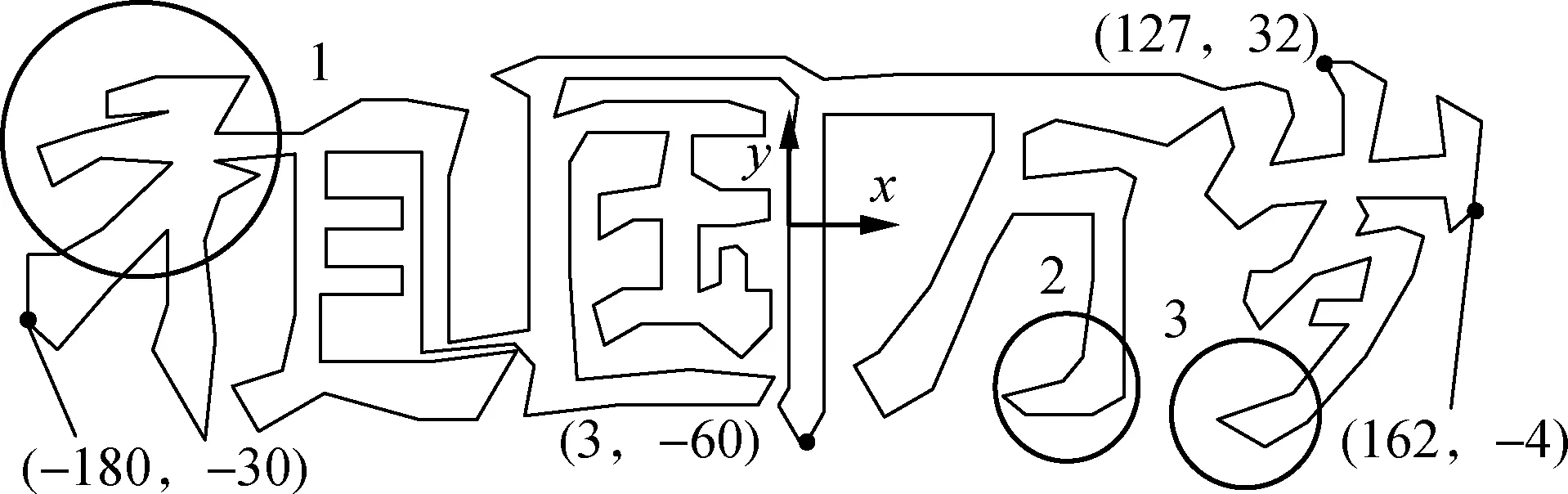
图7 动平台目标轨迹及部分坐标(单位：mm)

预先调整好纸平面高度,使得安装好的马克笔刚好接触纸平面,分别采用位置控制和力位混合控制策略将控制程序下载到Arduino控制器,使得机器人动平台按照预设轨迹运动。选取图7中的1、2、3位置进行对比，结果如图8所示，其中红线为目标轨迹，黑线为实际轨迹。

图8 实际曲线精度对比

对图8进一步分析,结果如表5所示。从图8和表5可以看出,动平台运动到图 8中的区域,由于靠近工作空间边缘,采用位置控制算法时柔索出现松弛的现象,导致无法精确定位,因此实际轨迹与目标轨迹相差较大;增加力控环节使实际的悬索张力基本与期望悬索张力保持一致,相比于张力优化算法[12],力位混合控制算法考虑了位置误差的影响因素,具有更高的定位精度。

表5 不同算法时轨迹曲线最大偏差 mm

5 结 语

针对普通悬索机器人位置控制精度不高、硬件成本高的问题,设计了一种小型平面四悬索机器人。结果如下:1)自主设计的收放绳结构可以精确保证绳索长度与电机转角的比例关系,简化了控制策略;2)利用电机内部传感器实现了精准力感知和力位混合控制,提高了位置控制精度;3)本文算法执行效率高,可运行在Arduino主控板、总线电机等低成本硬件平台上，具有一定的应用价值。