新型磁流变阻尼器的研制及其准静态分析

刘月辰，王强，刘明斗

(中国海洋大学工程学院，青岛 266100)

磁流变液(magneto-rheological fluid, MRF)作为一种智能材料，在过去的几十年中受到了广泛的关注。磁流变流体是电流变流体的磁性类似物，通常由微米大小的磁极化颗粒分散在载体介质(如矿物油或硅油)中形成[1]。研究表明，磁流变液在磁场作用下，可以在短时间内从牛顿流体转变为黏塑性流体。随着磁场强度的增大，磁流变液的屈服剪应力增大[2]。

磁流变阻尼器(magneto-rheological damper, MRD)是磁流变液应用装置之一。与传统的阻尼器相比，磁流变阻尼器具有能耗低、出力大、响应快速、阻尼力连续可调等优点[3]，现有的磁流变液阻尼器根据结构形式、磁流变液工作模式和节流通道构型等，可以分为单出杆流动式、单出杆混合式、双出杆混合式和双出杆旁路式等类型[4-5]。

这些磁流变阻尼器已经得到深入的研究，在车辆工程、土木结构、海洋平台、武器装备等领域已显示出广阔的应用前景[6]。

磁流变阻尼器作为一种新型的设备，它能很好地满足地震应用的要求和限制，具有非常低的功率要求。与传统被动阻尼相比，磁流变阻尼器具有良好的半主动控制特性，结构不同表现出来的隔振特性也不同[7]。自1996年以来，MRD的研究得到了进一步的发展。

Spencer等[8]在单杆流动磁流变阻尼器的基础上，对磁流变阻尼器的控制进行了大量的研究，使磁流变阻尼器在土木工程中的应用取得了很大的进展。磁流变阻尼器的结构参数决定了其体积和功耗，所以，参数的选择是影响磁流变阻尼器性能的重要因素。刘旭辉等[9]为解决应用于假肢膝关节的MRD的问题，结合MRD的参数研究，分析和优化了两者存在的关系；张丽霞等[10]基于Pareto集多目标方法和NSGA-Ⅱ遗传算法研究了研究参数对磁流变阻尼器减振的影响。

尽管如此，它在高冲击环境下的使用效果不佳。在高冲击环境下，要求阻尼器有较大输出阻尼力的同时，还要有高可调阻尼比来吸收冲击载荷。但是，现有的磁流变阻尼器由于结构的限制，使其难以同时满足大输出阻尼力与高可调阻尼比的需求。现存的磁流变阻尼器研究应用除双出杆旁路式之外，其他结构的磁流变阻尼器的节流通道的横截面积与活塞的大小及阻尼器的其他尺寸是关联的，不能独立设计。而传统的双出杆旁路式的磁流变阻尼器由于节流通道外置导致外型尺寸过大。

综上所述，目前在冲击环境下使用的高可调阻尼比的磁流变阻尼器结构复杂，尺寸和行程太大。为提高磁流变阻尼器的抗冲击效果，获取较大的阻尼力和可控倍数，现系统地论述新型双出杆磁流变阻尼器的结构设计原理、力学模型建立过程，通过实验数据与理论计算结果对比验证力学模型的准确性，建立的准静态模型以期为新型磁流变阻尼器的设计提供设计公式指导。

1 新旧磁流变阻尼器的结构分析

1.1 传统磁流变阻尼器

Spencer等[8]为了研究磁流变阻尼器在土木工程中的应用，以典型的双出杆剪切阀式磁流变阻尼器为研究对象，研究了其力学模型，提出了其输出可控阻尼力Fτ、黏性阻尼力Fη以及动态范围D的表达式，为以后磁流变阻尼器的研究提供了宝贵的研究经验。

Spencer[11]在对于磁流变液阻尼器的准静态分析中，提出了以下假设：①磁流变液阻尼器以恒定速度运动；②磁流变流体流动充分；③可以用一个简单的Bingham塑性模型来描述磁流变流体的行为。并基于平行板模型给出了关于磁流变阻尼器各参数的简单方程[11]，即

(1)

(2)

(3)

式中：Fτ为库仑阻尼力，N；c为库伦阻尼修正系数；τ0为剪切屈服应力，N/m2；L为活塞的有效长度，m；Ap为活塞的有效面积，m2；h为间隙宽度，m；sgn为符号函数，其值为1、0或-1；v0为活塞头的速度，m/s；Fη为黏性阻尼力，N；w为阻尼器环形流道周长，m；Q为体积流量，Q=v0Ap；η为屈服后塑性黏度，Pa·s。

图1为传统的双出杆剪切阀式磁流变阻尼器结构简图。如图1所示，节流通道为活塞与内筒内壁之间的间隙，其面积与活塞的大小直接关联，由阻尼力计算公式(1)～式(3)可以看出，不可控的黏性阻尼力，会随着节流通道面积的减小、活塞速度的增大而增大，使得磁流变阻尼器的可调阻尼比降低，在高速冲击下的缓冲性能降低，不适用于高速冲击缓冲控制。

L1为活塞有效长度；V为活塞杆速度；R为MRD外径；d为活塞杆直径；h为间隙宽度

1.2 新型磁流变阻尼器的方案设计

针对以上传统磁流变阻尼器的限制以及外回路式磁流变阻尼器结构尺寸大的问题，提出一种节流通道外置的双出杆磁流变阻尼器，以可调阻尼倍数高、输出阻尼力大且结构紧凑为标准，设计其结构简图如图 2所示。

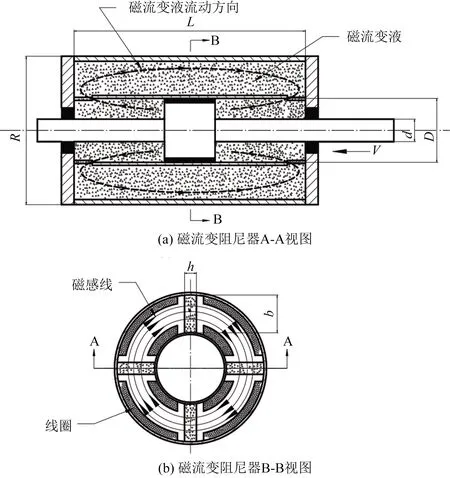
D为MRD内径；b为矩形狭缝宽度

MRD节流通道外置，若干条节流通道分布在整体铁芯(整体铁心由内外筒壁包围)之内为矩形狭缝，这样可以在阻尼力与可调阻尼比能够单独设计的同时，使磁流变阻尼器保持较为紧凑的结构。

2 新型磁流变阻尼器流动模型分析

2.1 节流通道内流速分布

传统的阀式磁流变阻尼器的节流通道为环形，磁流变液在节流通道内的流动可以看作流体在两平行板间的流动。图3给出了流过平行板的磁流变液速度分布。当磁流变液流过平行平板时，在1区和3区，磁流变液剪切应力大于其屈服应力，磁流变液受到剪切力的作用存在剪切流，此区域称为屈服区。在2区，磁流变液的剪切应力小于屈服应力，不存在剪切流，液体像塞子一样以相同的轴向速度运动，这个区称为塞流区，又称为未屈服区[12]。

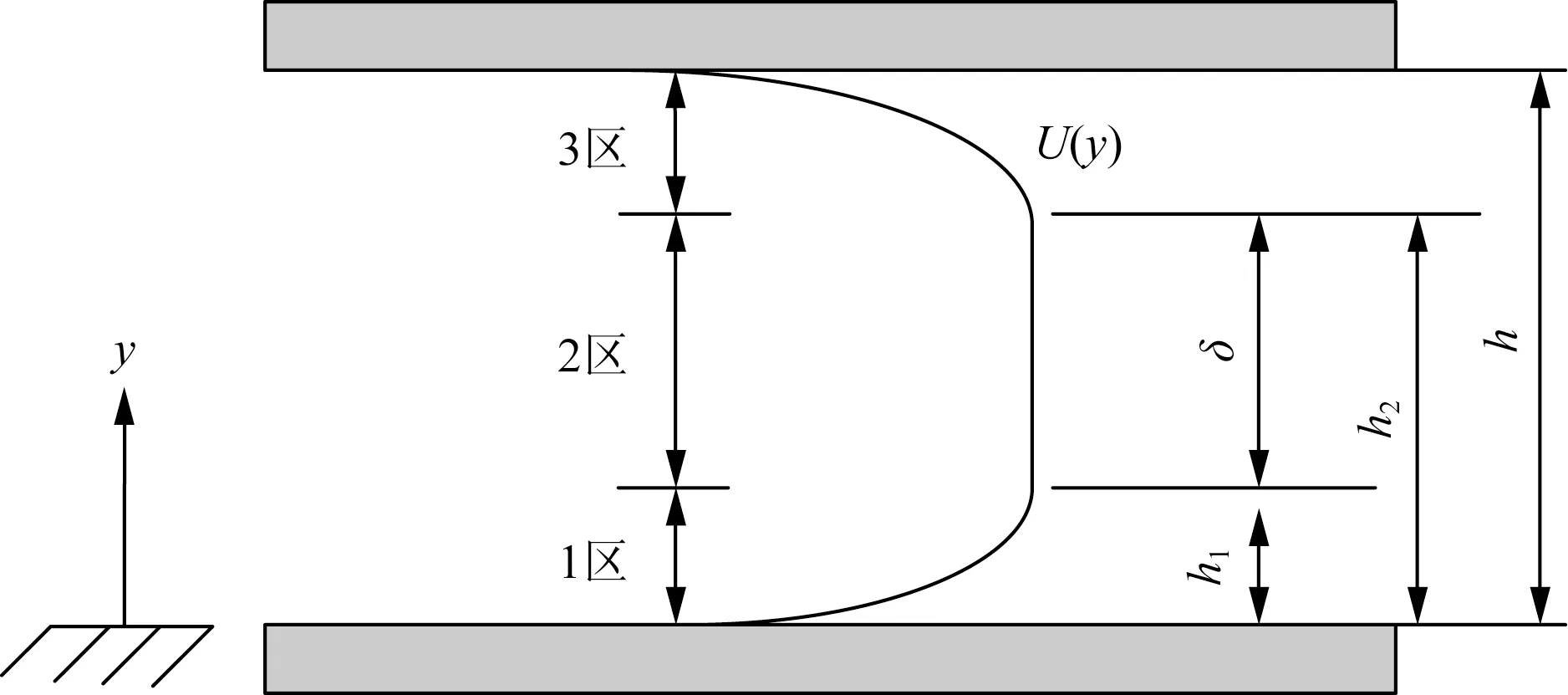
U(y)为平行板间液体流速；δ为2区的宽度；h1为1区宽度；h为平行板间距；h2=h1+δ

2.2 基于Herschel-Bulkley模型的节流通道内磁流变液准静态建模

下文将讨论基于Herschel-Bulkley模型的MRD的静态建模。相应的本构关系表达式[13]为

(4)

对于新型磁流变阻尼器的节流通道，近似看作平板流动模式进行分析，磁流变液流动状态为层流，根据N-S方程，流体的运动方程为

(5)

式(5)中：u(y)为磁流变液流动速度，m/s；ρ为磁流变液密度，kg/m3；τ为剪切应力，N/m2；p为间隙内磁流变液压强，Pa；x、y为两方向的位移。

由于磁流变液质量较小，所以在不考虑惯性力的情况下，对准静态建模的精度基本无影响。又节流通道间隙很小，对于流动模式，式(5)可简化为

(6)

(7)

式(7)中：D为由边界条件确定的常数。

(8)

又由速度边界条件u(y=h)=0，对式(8)进行积分得到区1内流速表达式(0≤y≤h1)为

(9)

(10)

再由区3内速度边界条件u(y=h)=0，积分得到区3内流速表达式为

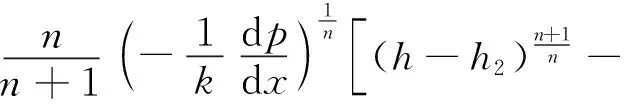
(11)

在区2内，塞流区边界流速满足：

u2(y)=u1(h1)=u2(h2)

(12)

利用式(10)～式(12)得到区2内流速表达式为

(13)

综上所述，得到平面内流速表达式为

(14)

2.3 体积流量和阻尼力

假设磁流变液不可压缩，由流体力学连续性原理，磁流变液流过节流通道的体积与活塞在内筒运动产生的体积相等，则流过节流通道的体积流量[14]为

(15)

式(15)中：m为节流通道狭缝数；b为矩形狭缝宽度。

展开得

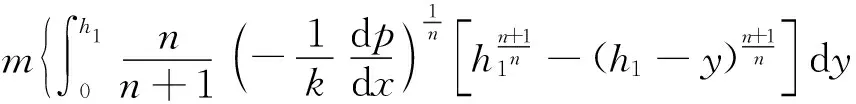
(16)

由剪切应力边界条件可得

(17)

将式(17)代入式(12)化简为

(18)

将式(18)代入式(16)整理可以得到流量的表达式为

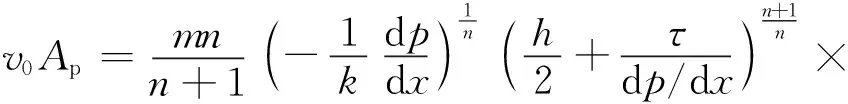
(19)

当n=1时，上述Herschel-Bulkely模型退化为Bingham模型，式(19)简化为

(20)

将式(20)进行无量纲化处理，定义无量纲量[15]为

(21)

(22)

(23)

式中：V为无量纲速度；Ρ为无量纲压力梯度；Γ为无量纲应力。

阻尼器的阻尼力计算公式为

(24)

将无量纲量替换式(20)的参数，可以得

m(Γ+Ρ)(2Γ+Ρ)ΓV2-ΓV2Ρ2=0

(25)

当V趋近0时，Р与Г满足：

(26)

式(26)的解可以通过数值方法得到，即

(27)

当Г趋近0时，Р=1/m。

所以，黏性阻尼力Fη可以表示为

(28)

定义磁流变阻尼器的动态范围D为可控阻尼力Fτ与黏性阻尼力Fη的比值，即

(29)

由于参数h与参数b相差两个量级，可以忽略由固壁引起的可控阻尼力，故可控阻尼力Fτ可定义为

(30)

从而，得到两种结构的磁流变阻尼器的可控阻尼力与动态范围表达式[14]，即

(31)

(32)

式中：Fτ2为新型磁流变阻尼器的可控阻尼力，N；c2为新型磁流变阻尼器的库伦阻尼修正系数；L2为新型磁流变阻尼器活塞的有效长度，m；Ap2为新型磁流变阻尼器活塞的有效面积，m2；D2为新型磁流变阻尼器的动态范围。

对两种磁流变阻尼器的结构进行等外型尺寸性能比较，建立间隙比(h/R2)与可控力Fτ和动态范围D之间的曲线。如图 4和图 5所示，其中新型磁流变阻尼器的尺寸取值为h=0.000 4 m，R=0.001 7 m，可以看出新型磁流变阻尼器的可控阻尼力和可调阻尼比都远高于常规阻尼器。

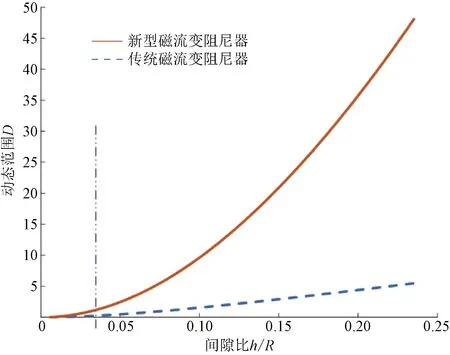
图4 传统MR阻尼器与新型MR阻尼器动态范围对比曲线

图5 传统MR阻尼器与新型MR阻尼器输出阻尼力对比曲线

3 新型磁流变阻尼器的制造

图6为本文提出的新型磁流变阻尼器的结构示意图。由图6可知，新型阻尼器两端通过关节轴承与外界相连，活塞杆两端伸出液压缸之外，为双出杆结构。新型阻尼器的节流通道外置，16条节流通道分布在整体铁芯之内。节流通道中磁流变液流动方向为阻尼器的轴向，线圈产生磁力线的方向垂直于节流通道的流动方向，保证磁流变效应的最大化，线圈铁芯有12组，如图 8所示，每1/4圆整体铁芯在轴向上均布3个线圈，其尺寸和位置根据磁场仿真优化设计得到，保证整个节流通道长度上磁场分布均匀。

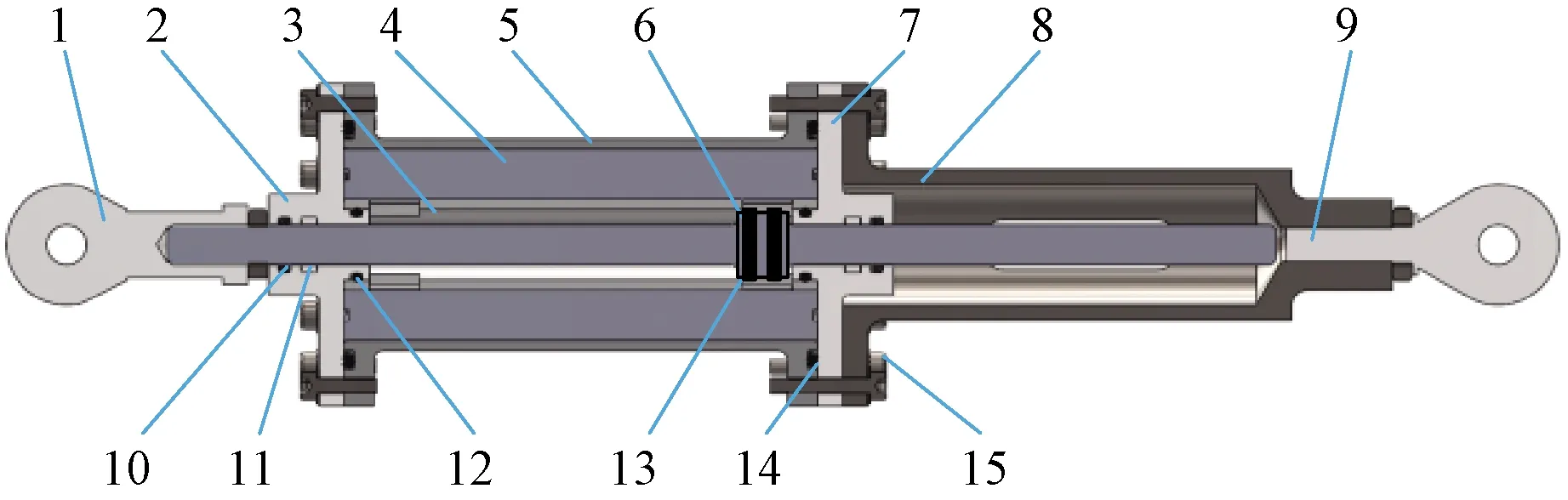
1为内螺纹球头轴承；2为上端盖；3为内筒；4为整体铁芯；5为外筒；6为活塞杆；7为下端盖；8为下端连接；9为外螺纹球头轴承；10为唇形密封；11为导向带；12为O型圈；13为格莱圈；14为O型圈

根据计算分析得到的新型磁流变阻尼器结构尺寸，查阅流体阻尼器的设计原则进行制图，设计加工完成阻尼器的主要零件如图 7所示。上、下端盖、内筒、外筒、活塞杆、下端连接选用7075铝合金，整体铁芯为电工纯铁；线圈根据最大电流要求选用0.3 mm漆包线制作，为保护漆包线，线圈外层涂抹一层绝缘漆；活塞处动密封选用格莱圈，活塞杆动密封选用唇形密封，上、下端盖与外筒之间的静密封选用O型圈，之间的连接靠外围均布的12个内六角螺钉进行连接，端盖中间设有导向套保证活塞杆运行平稳。

1为下端连接；2为下端盖；3为活塞杆；4为整体铁芯；5为外筒；6为上端盖

图8为新型磁流变阻尼器的整体铁芯的示意图，整体铁心分布有16条节流通道，每1/4圆分布有3条，2为绕线铁芯。

1为节流通道；2为铁芯；3为埋线槽

新型磁流变阻尼器较传统磁流变阻尼器，有更小的黏性阻尼力，更大的可控阻尼力，由于节流通道外置，可根据需要自由设计所需的可调阻尼比，结构体积、行程较传统磁流变阻尼器在同等阻尼力、可调阻尼比下更加紧凑。此新型磁流变阻尼器已获得了国家发明专利授权：201511011227.7。

4 力学模型的实验验证

本实验应用的是美国美特斯(mechanical testing & simulation，MTS)Landmark伺服液压控制测试系统，工控机装有MTS TestSuite软件。液压机行程为0～250 mm，最大受力可以达到100 kN。配套的力传感器为661力传感器。实验系统如图 9所示：新型磁流变阻尼器通过上、下夹具安装在MTS液压试验机上，通过直流稳压电源对阻尼器进行供电，液压作动器从下方对阻尼器进行激励，液压站为液压作动器提供液压源。激励信号通过工控机进行控制，力传感器固定在上夹具上方来拾取力信号，测得力信号通过工控机进行后续处理。

1为液压站；2为稳压电源；3为下夹具；4为阻尼器；5为上夹具；6为力传感器；7为冷却站；8为工控机；9为作动器

测试中采用三角波位移信号为激励信号，速度平稳，便于数据处理。系统中配套的MTS TestSuite软件可以完成信号频率及信号幅值的控制。将在试验机能达到的激励范围内对阻尼器在不同速度下的工作特性进行充分测试。同时试验机横梁可以上下移动，能够保证对阻尼器从其行程中间进行激励，磁流变阻尼器在试验机上的安装如图 10所示。

图10 新型磁流变阻尼器在试验机上的安装

在准静态测试时，采用三角波位移信号进行激励，每组电流、频率下，采集活塞通过平衡点时的速度和对应的阻尼力，稳定时的6次循环取平均值作为测试值。激励速度随激励信号幅值及频率的增大而增大，根据试验机激励信号能达到的最大速度，可以测得最大速度内阻尼器输出力与速度的关系曲线。

准静态测试测得的阻尼力主要包括黏性阻尼力、可控阻尼力以及摩擦力三部分。黏性阻尼力跟速度相关，且随着速度的增大而增大，可控阻尼力与磁场强度即通电电流相关，电流越大可控阻尼力越大，达到一定值会产生饱和现象。摩擦阻尼力可以在完成阻尼力测试后将阻尼器内磁流变液倒出，采用相同的测试方法再进行摩擦力测试。将第一次测得的阻尼力减去摩擦力即可得到黏性阻尼力和可控阻尼力的实测值。

上文推导的阻尼力计算公式中有大量参数，其中结构参数将阻尼器拆卸后重新测量获取，新型磁流变阻尼器为双出杆结构，阻尼力计算过程中用到的具体尺寸参数如表 1所示。

表1 新型磁流变阻尼器主要结构参数

通过有限元素法磁力学(finite element method magnetics，FEMM)磁场仿真软件计算得到的磁场强度值，加以研究MRF-122EG磁流变液剪切屈服强度与磁场强度关系曲线，可以得到每个磁场强度下对应的剪切屈服应力值，如表 2所示。

表2 不同驱动电流下磁场强度与剪切屈服应力值

根据上文建立的准静态模型，将整理后的参数代入到准静态模型中，可以得到新型磁流变阻尼器在不同通电电流下，输出阻尼力与速度的关系曲线，如图 11所示。

如图 11所示，本文建立的阻尼力计算公式能较为准确地计算出新型磁流变阻尼器在不同通电电流和活塞速度下的阻尼力，这证明本文建立的准静态模型能较为准确地计算出新型阻尼器的输出力大小。

图11 准静态阻尼力实测值与理论计算值的对比

然而，随着电流的增大，理论与实验的数值的差距逐渐增大，这可能是实际磁场效果与磁场仿真结果相差较大，磁场饱和现象无法很准确的表达，实际绕线时存在误差。其次造成实验数据较小的原因是在阻尼器加工过程中，狭缝尺寸h由于线切割的问题造成尺寸过大而且不均匀。

5 结论

设计了一种新型磁流变阻尼器，并对新型磁流变阻尼器进行了准静态实验研究，得到了输出力-速度曲线，对试验结果进行了分析。发现新型阻尼器用传统静力学阻尼力求解公式求解阻尼力存在误差，从阻尼器结构原理及流体力学理论出发分析了误差原因，根据流体力学理论，基于Herschel-Bulkley模型，建立了磁流变液的流动方程，针对新型磁流变阻尼器建立了准静态模型。在流体行为指数取1时，求得了新型阻尼器输出力与通电电流及速度的关系，并将准静态模型计算结果与实验结果进行了对比分析，验证了准静态模型的准确性。

(1)准静态实验结果显示新型阻尼器输出力-速度曲线斜率很小，达到了输出阻尼力大且可调阻尼比高的设计初衷。

(2)新型阻尼器节流通道内流度分布具有独特性，现有的准静态模型不能准确反映输出阻尼力，需要重新对其进行准静态分析及建模。

(3)基于Herschel-Bulkley模型建立的准静态模型计算结果与实验结果基本吻合，验证了准静态模型的准确性，并解释了偏差存在的原因。