引导滤波和对数变换算法融合的多尺度Retinex红外图像增强

陈文艺，杨承勋，杨 辉

（1.西安邮电大学 现代邮政学院，陕西 西安 710061；2.西安邮电大学 电子工程学院，陕西 西安 710121）

0 引言

与可见光成像相比，红外成像设备的优势在于环境适应力强、穿透力高，被广泛应用在各个方面，最早出现在军事领域[1-2]。红外图像的缺点是边缘模糊，对比度差和噪声大。因此，有必要研究红外图像增强算法以优化图像。传统的红外图像算法分为空域处理和频域处理，空域算法主要是直方图均衡化处理[3]和一些线性变换法。频域最常见的是Retinex 算法[4]和小波变换[5]法以及两种算法的深入研究。

在Retinex 算法的基础上众多的改进算法层出不穷，Jobson Daniel J.、Rahman Zia-ur 等人在1997年提出的中心环绕Retinex 算法[6]模型简单且使用广泛，核心内容是使用低通滤波函数与原始图像卷积来估算照明分量。由于单尺度算法的难点在于尺度因子的选择，Rahman 等人提出了一种基于单尺度算法的多尺度Retinex（multi-scale Retinex,MSR）算法[7]，该方法已经被很多学者通过不同比例的滤波函数应用进行了图像研究。被视为是许多不同尺度的SSR（单尺度Retinex）算法的加权求和。基于MSR 算法，研究者们提出了众多改进方法[8]。任崇巍等人用双边滤波代替高斯滤波[9]，在货车故障轨边图像检测系统中，改进了图像光照不均匀的问题。常戬等人针对传统Retinex 算法存在的泛灰、光晕、边界突出以及高曝光区域细节增强不明显等缺点，提出了改进双边滤波Retinex 的多聚焦图像融合算法[10]。王秋云等人将色彩模式RGB 转换至Lab，仅对亮度分量L采用引导滤波代替高斯滤波的改善多尺度Retinex 增强处理[11]，有效地提高了图像的质量。杨福豪等人针对水下图像存在的色偏、雾状模糊、低曝光和非均匀光照问题，提出基于色彩衰减补偿和Retinex 的水下图像增强算法[12]。本文针对红外成像技术采集到图像对比度低、边缘模糊的缺点，提出了引导滤波和对数变换算法融合的多尺度Retinex 红外图像增强。

1 相关理论

1.1 引导滤波

用局部线性模型来定义引导滤波。某函数上一个点与其相邻点具有线性关系，一个复杂函数可以用多个局部线性函数代替，如式(1)：

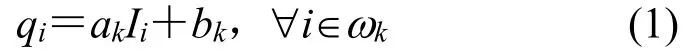
窗口中心位于k时，ak和bk是线性函数的系数；输出图像的值由q表示，I是输入图像的值；长度为r的局部矩形窗口表示ωk。输入图像可以是待滤波图像，也可以是另一图像，即引导图像。在(1)式两边同时取梯度：

式中：∇为梯度算子，当输入图像I有梯度时，输出q也有相似的梯度，也就是说，引导滤波器具有边缘保持特性。为了最小化真实值p和拟合函数输出值之间的差异，也就是让(3)式最小：

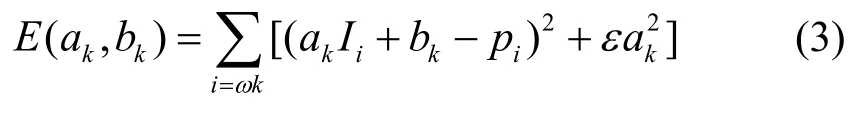
式中：ε是防止ak过大和控制滤波效果的重要参数，待过滤的图像p。用最小二乘法可以获得最优解的ak、bk：

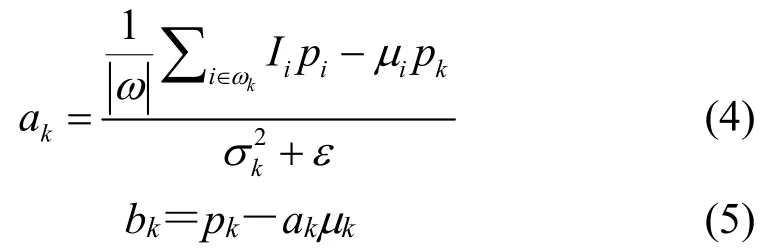
式中：σk2为引导图像方差，引导图像均值μk；待平滑的像素点为pi；窗口中像素数总和为；待平滑图像的均值为pk；ε为线性回归系数，决定了滤波器的平滑度。如果用原始图像来代替引导图像，则式(4)、(5)可以代替为：

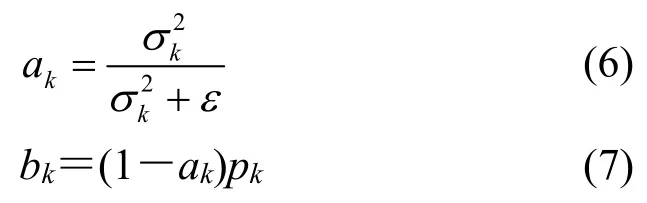
式中：图像的多个窗口中包含一个像素，并且不同窗口中的系数ak，bk不同，因此取这些窗口中的系数的平均值，来代替公式(1)中的ak，bk获取输出图像。

1.2 对数变换

对数变换改善了图像窄带区域的灰度分布，将窄带区域的低灰度部分扩展到了高灰度输出，图像低灰度信息就得以增强。同时，对数变换可以很好地压缩图像动态范围变化较大的像素值，目的是突出需要的细节。表达式如下：

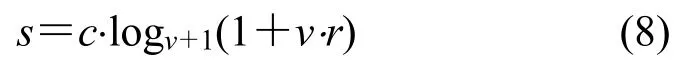
式中：c为常数；v越大灰度提高越明显；r为灰度归一化后的图像。

1.3 多尺度Retinex（MSR）算法

由人类大脑皮层形成的有关目标物体的颜色信息与外部光强度无关，但是与目标物体表面的反射特性息息相关。那么就可以将图像分成两部分，光照分量L(x,y)和反射分量R(x,y)，人眼感受到的图像可以表示式(9)：

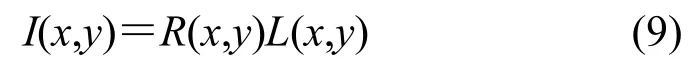
式中：L(x,y)表示图像背景包含的低频分量；R(x,y)表示图像的高频分量和物体反射特性，表现为图像的细节成分。因为对数模型与人类视觉特性相符合，从上式中看出，最后观察到的图像只要去除照度分量，就可以获得物体本身的信息。所以在对数域中对其进行计算，将简化(9)式，得到式(10)：

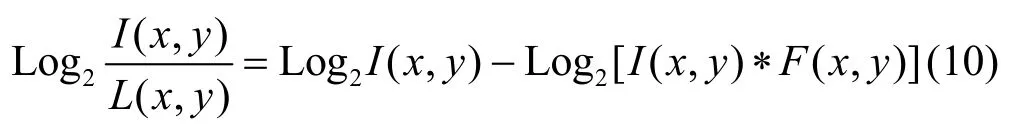
式中：低通滤波器F(x,y)一般为高斯函数也称为中心环绕函数。I(x,y)*F(x,y)表示输入图像与低通滤波器卷积，用来估计对图像低频部分。

上述式(9)、(10)推导出了单尺度Retinex（SSR）算法，为了解决SSR 的局限性，提出多尺度思想。可以将不同尺度参数SSR 算法的加权和看作是MSR 算法。光照分量L(x,y)是由不同比例的中心环绕函数与原始图像卷积后获得，然后去除L(x,y)是将其转换到对数空间进行运算。计算方法如下式(11)：

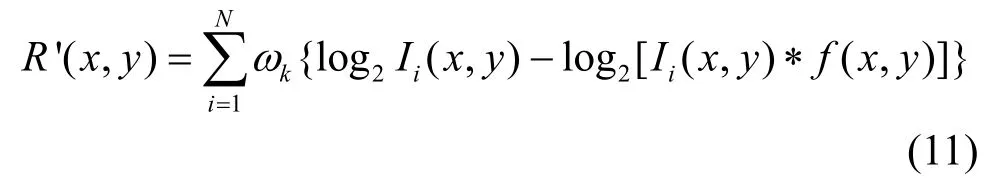
式中：ωk为权重参数，表示第i层的权重数值；Ii(x,y)为第i层图像信息；*为卷积符号；f(x,y)为中心环绕函数。最后，与光照信息无关的反射分量R(x,y)是由R＇(x,y)做反对数变换得到。计算式如(12)所示：

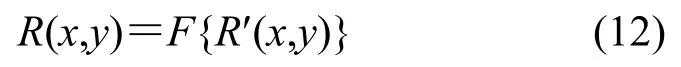
式中：F{}表示反对数变换。

2 基于引导滤波的多尺度Retinex 算法

2.1 本算法的具体步骤

针对经典MSR 的不足，提出引导滤波和对数变换算法融合的图像增强算法。流程图如图1所示。其具体步骤如下：

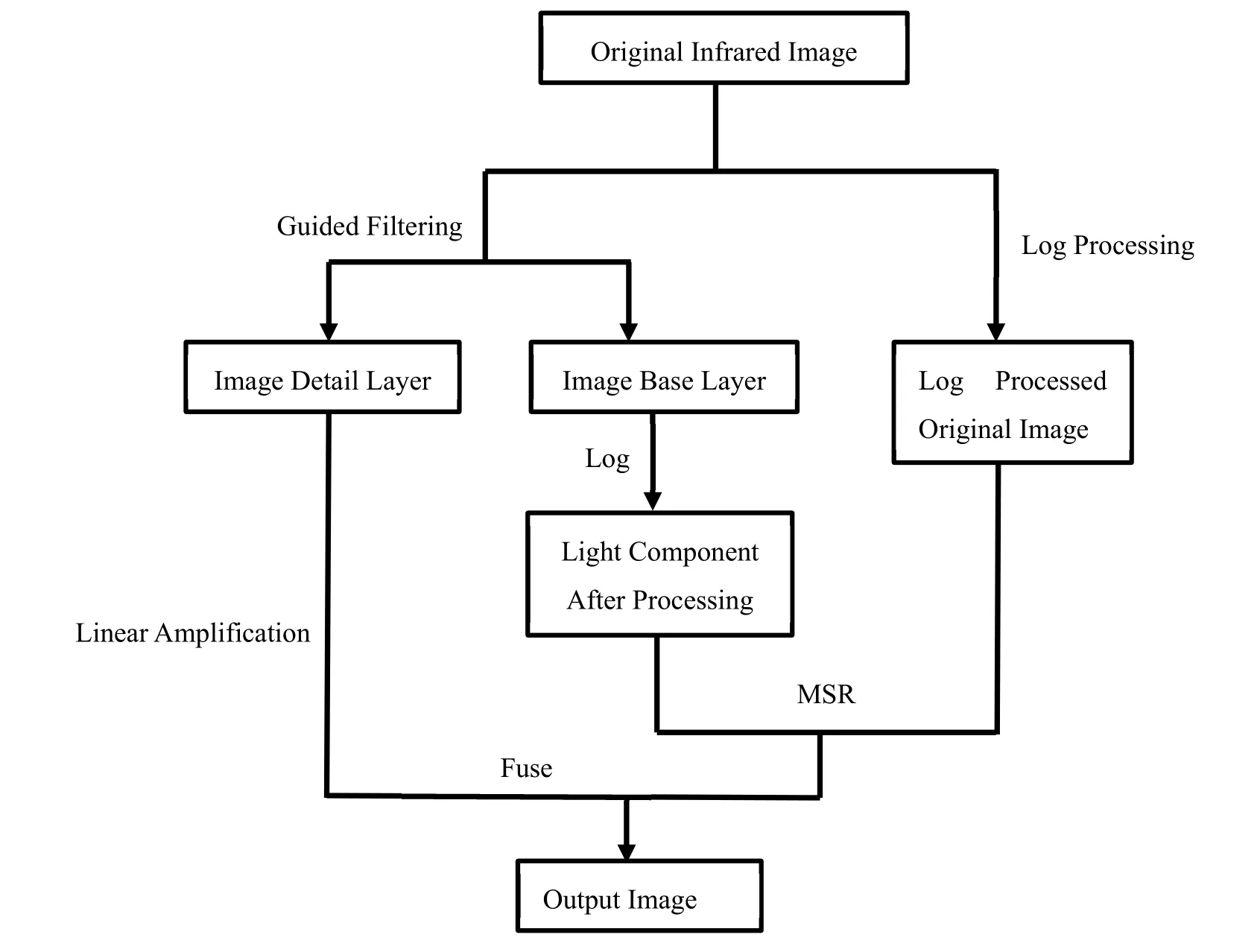
图1 本文算法流程图Fig.1 Algorithm flow chart of this paper

①首先原始图像用引导滤波进行光照分量估计得到图像的基础层；另外原始图像在对数域处理保持不变。

②将①步骤中的基础层图像作对数变换处理的结果，再进行MSR 算法得到算法处理结果；

③得到图像的细节层；原始红外图像减去步骤①中获取的基层图像，得到图像的细节信息；

④对细节层图像进行线性放大，与步骤②的处理结果叠加，得到最终的图像结果；

2.2 光照分量估计

原始的高斯滤波替换为引导滤波，以尽可能准确地估计光照分量。分配滤波器权重时，高斯滤镜仅考虑像素之间的距离，像素的灰度信息被忽略了，就导致灰度阶跃变化，即图像边缘滤波的结果不准确，因此不能准确地估算光照分量。根据本文介绍的引导过滤具有边缘保留和梯度保留的特征，用引导滤波来估计，可以更准确地估计光照分量。其表达式为：

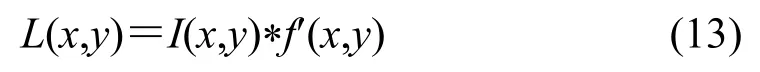
式中：f＇(x,y)表示引导滤波函数，其具体计算过程如(1)式所示；*表示卷积；I(x,y)为原始红外图像；L(x,y)估计的照度分量。引导滤波对原图平滑之后的结果与高斯平滑作对比如图2所示。

图2 高斯滤波与引导滤波效果对比图Fig.2 Comparison between Gaussian filtering and guided filtering

2.3 本文改进的MSR 算法

在获取光照分量的基础上用对数变换对其处理。对数函数是一个递增函数，对高灰色区域的峰值有抑制作用。对数函数符合人眼对灰度的响应的同时还可以保留细节，减小高动态范围图像的动态范围。

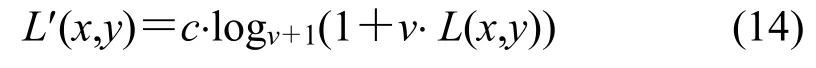
式中：常数c＝1，L(x,y)为引导滤波估计的照度分量，L＇(x,y)是对数变换处理后的照度分量。经过大量实验数据论证，v的取值在5～15 范围内，本文算法中，v取值为5 是增强效果达到最佳，v的值不宜过大，防止造成过度饱和。

通过MSR 算法处理图像，这里的MSR 算法是经过引导滤波替换后的改进算法。得到算法的处理结果，如式(15)所示：

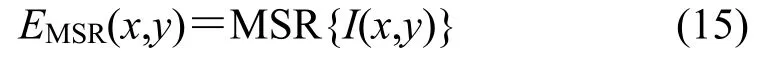
设输入图像为I(x,y)；改进后的多尺度Retinex 变换MSR{}，计算公式如(11)所示；通过计算得到增强结果EMSR(x,y)；多尺度加权求和的权重ωk，分别是来自R，G，B 三通道上的，各占1/3。

图像细节层的获取是由原始图像减去基层L(x,y)，获得包含了边缘、纹理的轮廓细节层N(x,y)，即：

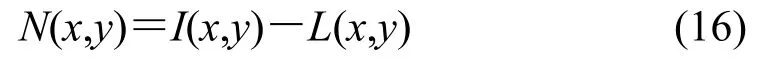
2.4 图像融合

通过式(15)、(16)求得图像的细节层N(x,y)和MSR增强后的红外图像EMSR(x,y)，将其融合得到最终增强图像的结果，即：

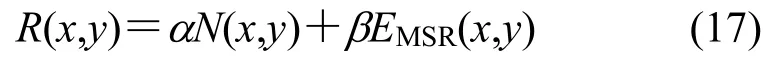
式中：α和β为调节权重占比的参数，调节细节层与红外图像的强度，通常α选择2～5，β一般选择1；R(x,y)为最终增强红外图像算法的处理结果。

3 实验结果及分析

为了让本文提出算法有效性得以验证，通过算法仿真实验，在客观评价和主观评价两个角度分析实验结果，并与传统MSR 算法、引导滤波算法作对比得出结论。以Matlab 2016a 软件作为辅助仿真工具，图3是本实验用到不同场景的红外图像。引导滤波中的引导图像选择原图，即为图像本身。

图3 实验仿真用到的红外图像Fig.3 Infrared image used in experimental simulation

3.1 主观评价

本文对3 个场景的图像分别进行实验，对其做MSR 算法增强、引导滤波增强、本文提出的算法增强，观察实验结果。

图4～图6分别是3 幅红外图像的增强结果。图4(a)，原图像中包含楼房的窗户和横跨的电线等细节信息，图像经过MSR 算法处理后，图4(b)所示未能凸显图像细节信息，并且整体图像对比度降低。图像经过引导滤波和本文算法增强后，图像整体对比度提升，并且细节信息也得到了增强，图4(c)和图4(d)中可以清晰地看到楼房窗户和横跨的电线，但是在引导滤波增强图像时，会产生光晕导致图像过度增强。

图4 不同算法对场景1 的处理结果Fig.4 Processing results of Scene 1 by different algorithms

图5原图中，包含了后方楼房的窗户和车流等细节信息。图5(b)是通过MSR 算法处理后的图像，观察图像整体对比度下降、细节信息没有被增强。图5(c)是图像经过引导滤波增强后，图像楼房的窗户和车流等细节信息都被明显增强，但是车窗户被过度饱和。图5(d)是本文算法增强的结果，背景的楼房窗户和云彩以及马路上的汽车都更加清晰，同时对比度也得到了很大的改善，视觉效果更好。

图5 不同算法对场景2 的处理结果Fig.5 Processing results of scene 2 by different algorithms

图6亦是如此，图6(b)为MSR 算法增强结果图像对比度下降，图6(c)为引导滤波增强结果，细节被增强但是过度饱和。图6(d)为本文算法处理结果，细节信息和对比度都被改善，视觉效果好。

图6 不同算法对场景3 的处理结果Fig.6 Processing results of scene 3 by different algorithms

根据对3 个场景的仿真验证，从主观角度分析来看，与其他算法相比，处理效果是显而易见的。下面根据算法流程图，利用场景1，对本文算法的每个步骤做仿真实验得出结果，如图7所示。

图7 按算法流程图处理的每个步骤图像Fig.7 Processing results of each step

3.2 客观评价

客观评估是对处理结果的优缺点进行量化分析。本文中用到的量化标准有：信息熵[13]、平均梯度[13]、峰值信噪比3 项评价指标。对MSR 算法、引导滤波算法以及本文算法进行性能评价。下面对这3 种评价指标做简单的介绍：

信息熵：它是图像质量评估的通用指标，从信息论的角度反映了图像信息的丰富性。通常，图像信息熵越大，信息越丰富，质量越好。

平均梯度：指的是图像的边界的灰度级变化率大，图像清晰度的衡量就是依据此变化率的大小。图中小细节对比度的变化率和图像的相对清晰度都可以用平均梯度衡量。平均梯度值大的，图像层越多也就越清晰。

峰值信噪比：是一个存在局限性对图形进行评估的客观标准。是最大值信号和背景噪声之间的差值。图像去噪效果好的标志是峰值信噪比的数值大于30 dB，而小于20 dB 图像去噪质量较差。

对图2中3 种不同场景的红外图像进行测试，场景1 在不同算法下的客观评价结果如表1所示。

从表1对场景1 的客观评价结果可以看出，改进算法与其他两种传统算法在信息熵、平均梯度的指标参数上都提高了，并且信息熵和平均梯度越大，说明图像的质量越好越清晰。峰值信噪比的数值都大于30 dB 表示处理后的图像质量是比较好的。再分别对场景2、场景3 的红外图像进行客观评价，结果如表2、表3所示。

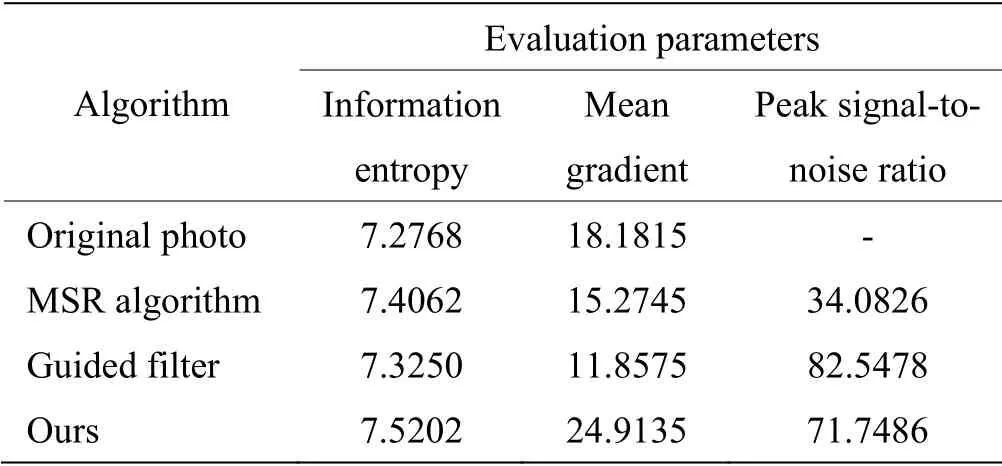
表1 场景1 客观评价结果Table 1 Scenario 1 objective evaluation results

在表2中可以看出，场景2 应用于MSR 传统算法时，效果并没有提升反而下降了。但在本文的改进算法中，依然具有独特的优势，在信息熵和平均梯度数值上高于其他两种算法。

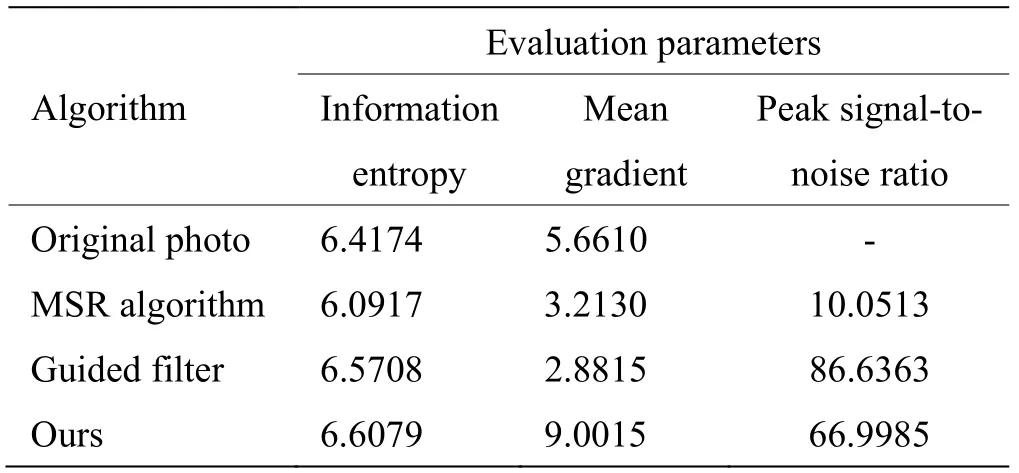
表2 场景2 客观评价结果Table 2 Scenario 2 objective evaluation results

分析表3，场景3 在本文算法的处理下，相对于其他两种算法信息熵有所提高，处理后图像的平均梯度也优于原图，这说明处理后图像质量被提高。峰值信噪比大于30 dB，图像质量并未失真。本文算法能够有效的增强图像质量。

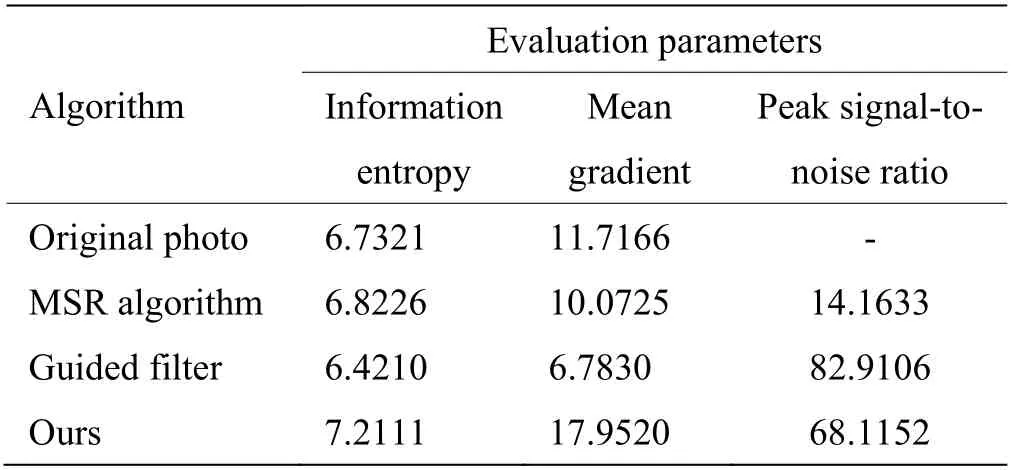
表3 场景3 客观评价结果Table 3 Scenario 3 objective evaluation results

4 结论

鉴于红外图像边缘模糊、对比度差的缺点，提出了引导滤波和对数变换算法融合的多尺度Retinex 算法。引导滤波代替高斯滤波有效的防止高斯滤波在增强图像过程中出现的边缘模糊现象。利用对数变换对获取的基础层进行处理，保留细节的同时降低了高动态范围图像的动态范围，提升了整体图像对比度。通过Matlab 仿真测试，与多尺度Retinex 算法、基于反锐化掩模的引导滤波算法相比，在主、客观方面分析，结果显示本文算法增强得到的红外图像，细节信息被增强的同时图像对比度也得到了提升。图像清晰可见，层次分明，视觉效果良好，达到增强图像的目的。