基于视轴矢量序列的目标轨迹确认方法

薛永宏，王铁兵，乔 凯，樊士伟

（北京跟踪与通信技术研究所，北京 100094）

0 引言

红外监视系统因其作用距离远、隐蔽性强而被广泛应用于各个领域。典型红外监视系统如美国天基红外系统（space based infrared system,SBIRS），包括地球静止轨道和大椭圆轨道两类卫星。目标轨迹确认是天基红外监视系统关键技术之一，参考文献[1-4]以地球静止轨道卫星为背景，采用“先图像配准、后确认分析”的策略，实现对目标像平面轨迹的确认。此类方法主要以地球静止轨道卫星为应用背景，相邻探测图像相对“静止”、帧间图像变化差异小、易于实现图像配准；当卫星运行于椭圆轨道时，探测图像随时间持续的缩放、旋转[5]，帧间图像差异变大，图像配准残差增大，上述方法对目标轨迹确认的错误率将增加。

以椭圆轨道探测条件下目标轨迹确认为研究背景，针对帧间探测图像畸变大、基于图像配准方法的轨迹确认误差大等问题，提出基于视轴矢量序列的目标轨迹确认方法，并利用GM-PHD（Gaussian mixture probability hypothesis density）滤波器对目标视轴矢量序列进行滤波，实现目标轨迹确认。

1 目标视轴矢量序列建模

1.1 视轴矢量建模

目标视轴矢量是指三维空间中从光学传感器口面中心点到目标点连线所形成的矢量，如图1所示。红外监视系统中，目标视轴矢量一般通过建立逆成像模型，利用目标在像平面位置、卫星轨道、姿态等参数计算得到。由于探测图像中的目标点既包括真实的目标点，也包括由杂波产生的虚假目标点；实际得到的视轴矢量集是真实目标视轴矢量和虚假目标（杂波）视轴矢量的合集。

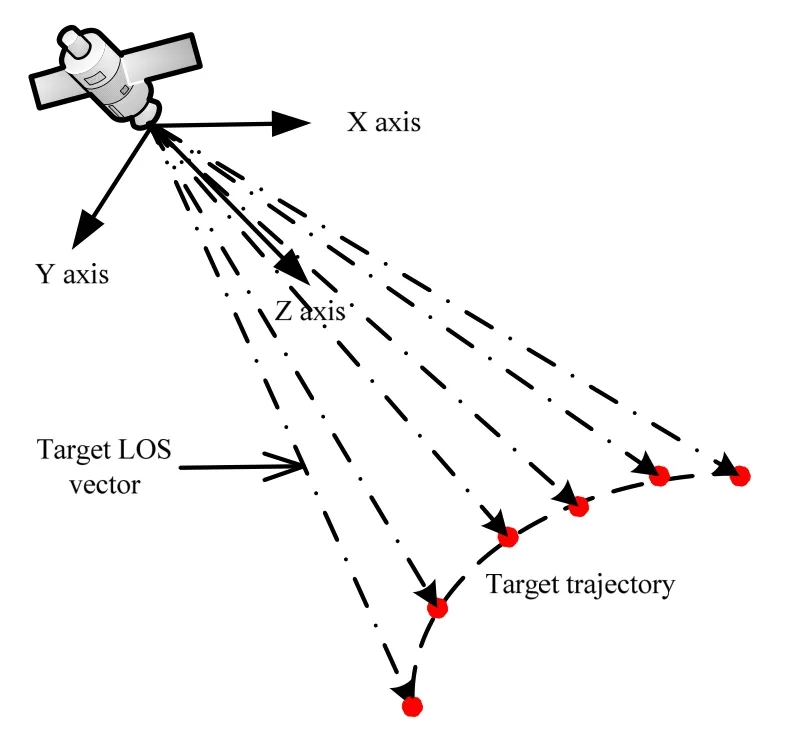
图1 目标视轴矢量示意图Fig.1 The sketch of target LOS vector

目标视轴矢量ueci,Tar通常可表示为：

式中：I为3×3 单位矩阵。由式(2)可知，目标视轴矢量的运动是卫星运动与目标运动的耦合。

通常卫星在空间的运动主要受地球重力的影响，可采用J2 或J4 模型表示[6-7]；目标则受推力、重力、空气摩擦力等多种力的作用[8]，且不同的力随时间变化的大小不同，因而一般采用动力学模型对其运动特性进行建模[9]。由于目标视轴矢量运动是卫星运动和目标运动的耦合，其运动可看作多种力作用下复杂的变加速运动，如式(3)：

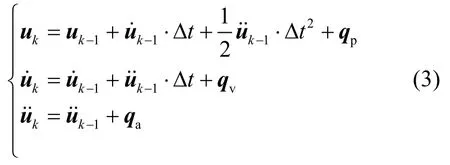
式中：qp、qν、qa分别为目标视轴矢量位置、速度、加速度扰动项；Δt为成像周期。同理，杂波在像平面表现为随机运动的位置点，其视轴矢量运动特性符合高斯分布，因此可利用目标与杂波视轴矢量运动特性差异，通过滤波进行目标轨迹确认。

1.2 状态转移模型

目标视轴矢量为一条指向特定方向的射线，视轴矢量长度的变化并不会对矢量所包含的信息产生影响。为降低计算复杂性，可对视轴矢量进行归一化降维处理，使得：

归一化后单位视轴矢量ueci,Tar可通过其任意两个坐标轴唯一确定。在椭圆轨道红外监视系统中，卫星轨迹与目标之间的距离较远，在ECI 坐标系下，目标视轴矢量的Z轴分量可近似认为是一个常数，因此可利用XOY平面内X轴和Y轴分量的滤波结果唯一确定单位视轴矢量ueci,Tar。降维后公式(3)给出的简化变加速运动模型可表示为：

目标视轴矢量状态转移模型即可表示为：

1.3 观测模型

基于视轴矢量进行目标轨迹确认其观测数据来源于单帧图像目标检测得到的疑似目标点，结合卫星位置、姿态角、传感器参数等解算得到视轴矢量，因此观测模型可构建为：

2 GM-PHD 滤波器及其改进设计

2.1 GM-PHD 滤波器

假设目标状态转移模型和测量模型均为线性高斯模型，即：

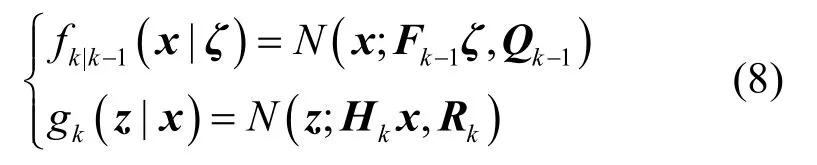
假设在k－1 时刻，目标状态函数为：

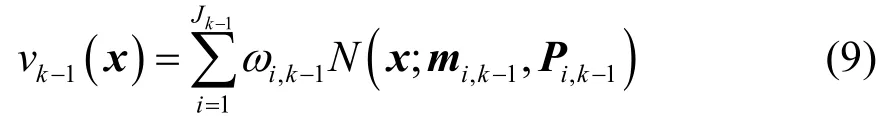
则在k时刻，预测的目标状态函数为：

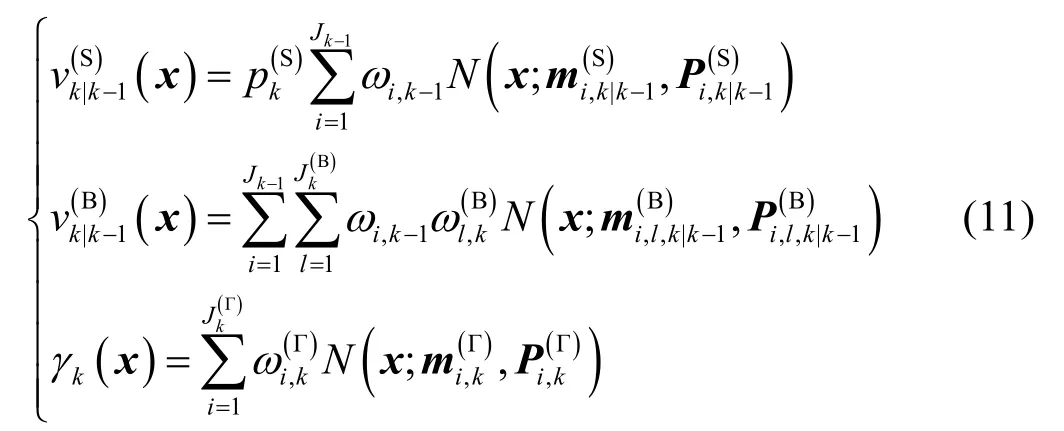
其中：

式中：Jk(B)和Jk(Γ)分别表示分裂目标和新目标的个数；ωl,k(B)和ωl,k(Γ)为对应高斯项的权重；pk(S)为目标的存留概率；dl,k－1(B)、Pi,k－1(B)、Ql,k－1(B)为分裂目标状态的先验信息。可以看出，预测的目标状态函数仍可写为高斯混合形式：

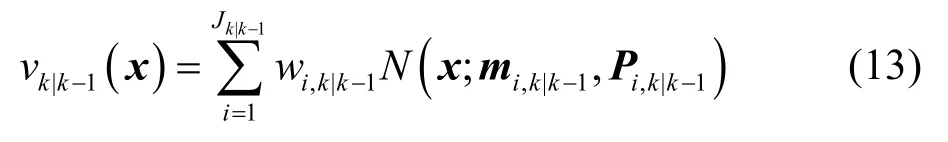
若k时刻，传感器的量测为zk，则更新后的目标状态函数为：

其中，第1 项表示漏检目标的PHD；第2 项表示利用检测到的目标更新后的PHD；且：

GM-PHD 滤波器目标状态更新滤波示意图如图2所示。

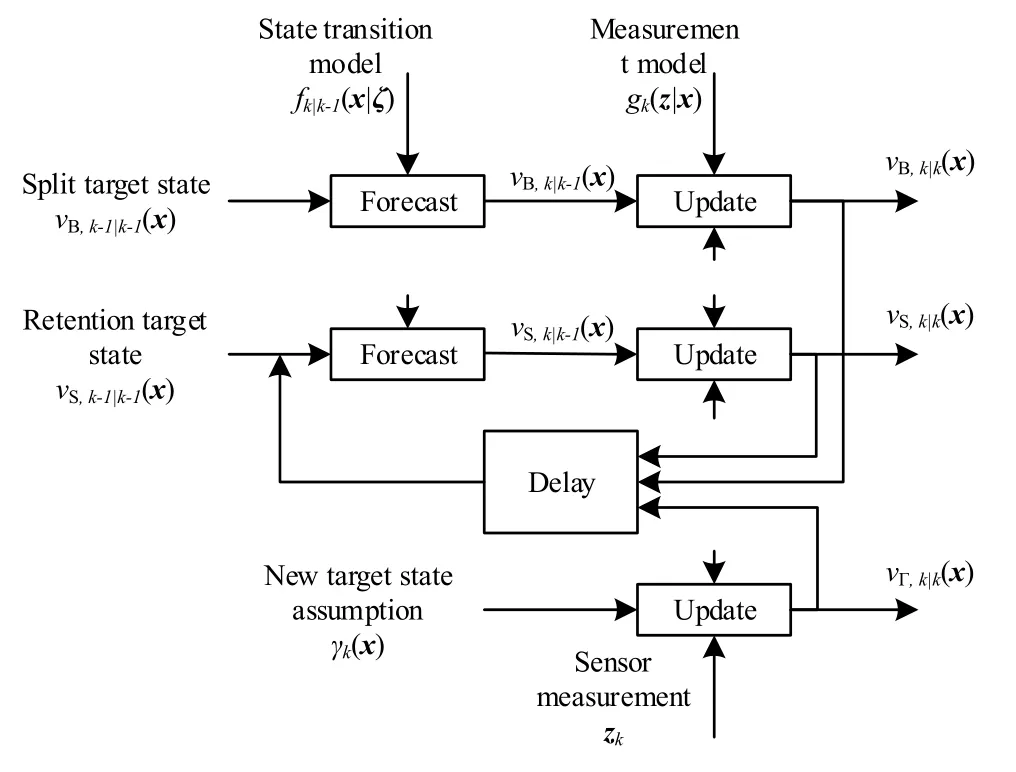
图2 GM-PHD 滤波器目标状态更新Fig.2 Target state update of GM-PHD filter

2.2 改进的GM-PHD 滤波器

根据GM-PHD 滤波器状态更新过程，通常新目标的状态信息仅包含在状态函数γk(x)中，将式(11)代入目标状态更新函数式(14)后，可将新目标状态更新公式简写为：

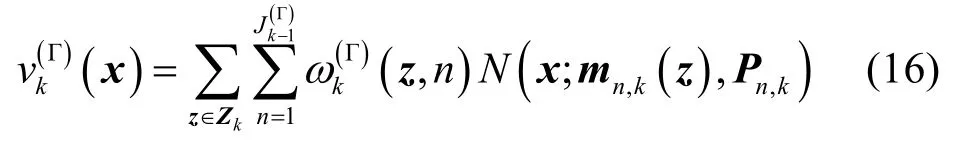
其中：

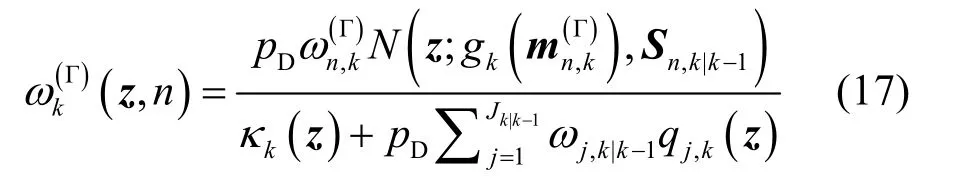
表征更新后新目标高斯项的权重。为减少计算资源的消耗，GM-PHD 滤波器即依据该权重对高斯项进行裁剪。以图3为例，式(17)中高斯项权重的更新，本质上为真实量测z和预测量测gk(mn,k(Γ))之间相关性的计算过程。当新目标位置等先验信息已知时，真实量测与估计的量测在测量空间的位置非常接近，相关性大，因而高斯项权重较大，目标不易于被剪除；反之当目标位置等先验信息未知时，二者在测量空间的距离一般较远，相关性小，高斯项权重也非常小，甚至接近于零，新目标易于被剪除而导致丢失。

图3 GM-PHD 测量空间似然函数Fig.3 Likelihood function of GM-PHD measurement

可以看出，GM-PHD 滤波器导致新目标丢失的一个重要原因就是假设的新目标状态与真实目标状态不符，进而导致在测量空间中，真实量测与估计量测距离较远所致。事实上，任何新目标都将会在传感器中产生量测，且由于目标运动速度有限，在相邻时间内测量空间中新目标量测距离将很近。因而，利用相邻时间历史测量状态直接假设为新目标量测状态，即将k－1 时刻传感器量测作为k时刻新目标量测状态的反馈滤波方式，可有效解决新目标丢失问题。新目标高斯项权重更新方式如下：

改进后的GM-PHD 反馈滤波器目标状态更新滤波示意图如图4所示。

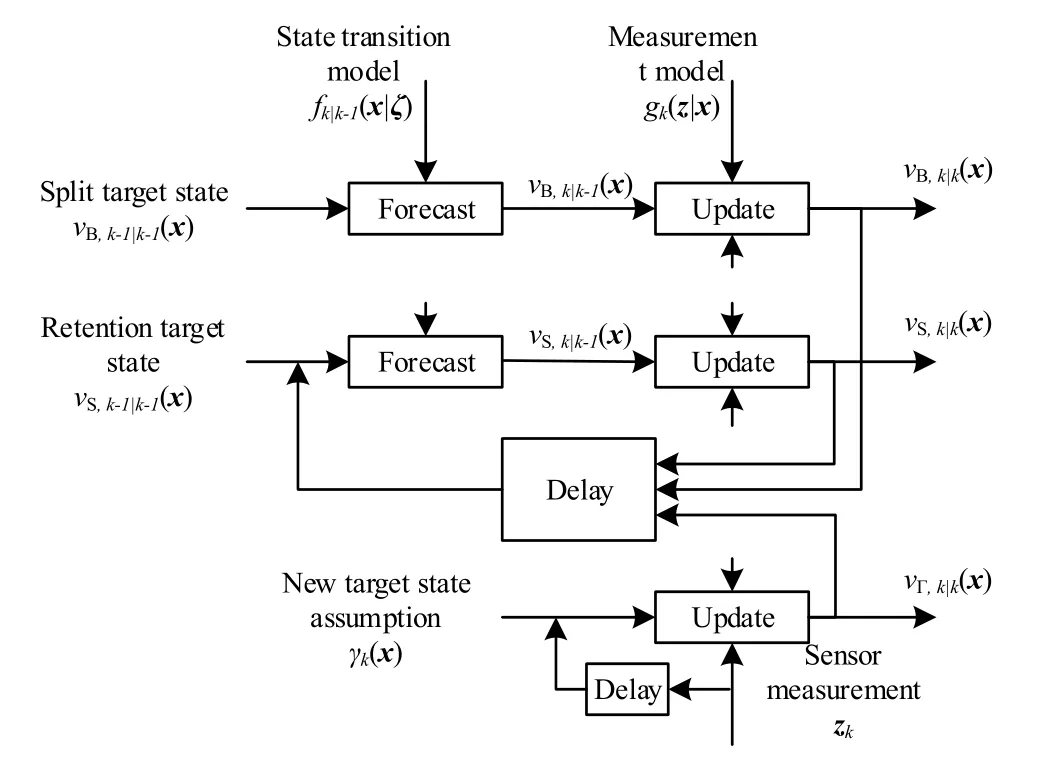
图4 GM-PHD 反馈滤波器目标状态更新Fig.4 Target state update of GM-PHD feedback filter

3 仿真试验

以一颗运行于Molniya 轨道的大椭圆轨道红外监视卫星为例，假定多目标场景。场景中包含3 个不同时刻，从不同位置发射的导弹目标，目标1 从仿真开始即出现，目标2 从仿真开始后40 s 出现，目标3 从仿真开始后80 s 出现。仿真中假设杂波密度κ(z)为10－5；成像周期Δt为5 s，像元角分辨率为60 μrad；卫星姿态确定误差为10''；经视轴矢量校正后，视轴矢量偏差为60 μrad。利用目标在像平面运动轨迹，解算后即可得到目标视轴矢量序列，对目标视轴矢量进行归一化并降低其维数后，得到序列目标视轴矢量在ECI 坐标系XOY平面的运动轨迹。目标运动轨迹如图5所示。

图5 目标运动轨迹Fig.5 Target trajectory

分别采用GM-PHD 滤波器（GM-PHDF）和改进的GM-PHD 滤波器（IGM-PHDF）对目标轨迹进行滤波；通过比较估计目标个数与真实目标个数的差异、估计目标视轴矢量与真实目标视轴矢量的偏差以及OSPA（optimal subpattern assignment）距离[13-14]对两个算法的性能进行评价。试验中Monte-Carlo 仿真次数为1000 次，两种滤波器对目标视轴矢量X和Y的估计结果以及Z轴解算结果如图6所示；两种滤波器对目标个数估计结果、平均视轴矢量偏差及OSPA 距离如图7所示。

图6 两种滤波器对目标视轴矢量的估计结果Fig.6 LOS estimation results of two different filters

图7 两种滤波器对目标状态的估计结果Fig.7 Target state estimation results of two filters

仿真结果表明：①基于GM-PHD 滤波器，利用序列目标视轴矢量进行目标确认分析是可行的，可实现对目标个数以及目标视轴矢量状态的估计；②改进后的GM-PHD 滤波器可在新目标出现后5 s 内得到所有目标的视轴矢量信息，从而及时地发现新目标；与之相比，传统的GM-PHD 滤波器可以在5 s内得到第一个目标和第二个目标的视轴矢量信息，但对于第三个目标则需在15 s 后才能得到其视轴矢量信息，发现第三个目标的所需时间多于改进的算法。

进一步比较两种滤波器对目标数量估计结果、平均视轴矢量偏差以及OSPA 距离可知：待发现目标后，两种滤波器对目标视轴矢量信息的估计精度相当；但改进后的GM-PHD 滤波器对目标数量的估计结果更为准确。

4 结论

目标视轴矢量序列运动特性与目标像平面轨迹运动特性相同，利用目标视轴矢量序列对目标轨迹进行确认分析，可有效解决椭圆轨道监视系统图像畸变大、基于图像配准的确认分析方法误差大等问题；改进设计的GM-PHD 滤波器可在目标状态未知条件下，快速、有效、准确地对新目标状态进行估计，避免了新目标丢失和确认时效性差等问题，从而实现目标快速确认。尽管论文所提反馈滤波器是在高斯混合模型下进行的，但是通过采用PHD 的EKF、UKF 或粒子滤波实现形式，也可推广到非线性、非高斯模型应用的场景之中。