基于PCA-GA-BP神经网络的水电机组状态异常辨别方法

罗正亮，潘虹*，赵雷，唐魏，郑源

(1. 河海大学能源与电气学院，江苏 南京210037； 2. 重庆航运建设发展有限公司，重庆400000； 3. 河海大学水利水电学院，江苏 南京210037)

当前水电机组运行过程中往往容易因工况变化复杂或零部件磨损引发机组异常状态运行，容易对机组以及电厂造成生产损失，故能够精准、高效地实现对机组异常运行以及机组状态快速辨别的研究变得尤为关键，对机组实际运行具有重要指导意义.传统机组异常辨别方法大多依据零部件表面情况进行推理，如振动、磨损等，或是依赖于机组员工检修经验，这种方法具有一定的直观性，但其缺乏科学的逻辑解释.在现今大部分电站运行中，更多依赖于多传感器收集数据，通过观测海量连续数据间的波动表现或是分解数据振动量，再将其作为特征变量输入已有数据结构基础上的分类模型以进行机组运行状态智能识别.但此方法未能实现对大量数据的深度挖掘或数据融合进而深层次研究数据波动，且人工观测数据波动易出现精度不高、效率低等问题，以至于无法达到机组异常识别的高精确性和快速性的要求.

目前，BP神经网络[1-2]作为机器训练学习用以分析海量数据、实现数据挖掘与融合的途径之一，被国内外学者广泛应用于各类模型预测或是故障分类领域.遗传算法因其模仿自然界生物进化规律而被应用于BP神经网络全局寻优参数，达到改善传统神经网络的目的.郭梦茹等[3]通过结合遗传算法与神经网络，实现多联机阀类故障诊断；王虹等[4]研究了遗传算法下，神经网络的支架跟机自动化进程；周璐婕等[5]、李泽宇等[6]则研究了遗传算法优化神经网络下更多旋转机械类与电路模型故障诊断与预测的实现.但在使用遗传算法优化BP神经网络过程中，需采用大量原始数据进行建模，样本数量过多时会导致计算效率降低，严重时易影响模型精度，而主成分分析法(PCA)因其可以分析多输入变量所反映数据样本信息，有效提取样本数据特征被应用于数据降维处理，进而克服BP神经网络在大量数据下局部收敛的弊端[7-8].

综上，针对神经网络在水力机械领域内的实际应用，文中提出基于主成分分析法下的遗传算法优化神经网络以实现智能识别机组异常状态这一方法，做到机组异常状态早期预警、实现初始海量数据线性无关特征变量提取、完成数据预处理.同时在BP神经网络挖掘海量数据具备自学习、自提取求解规则与自适应能力的基础上，将其与遗传算法所结合，实现对神经网络输入层与隐含层之间权值与阈值的优化，有效提高BP神经网络学习与预测能力，避免陷入局部极小化、收敛不充分等问题.最后，通过电站机组传感器数据进行仿真训练，进行机组异常状态识别，以验证文中方法在精度与效率上所具有的优异性.

1 神经网络模型理论基础

1.1 BP神经网络原理

BP神经网络作为一种监督型、前馈型神经网络，具备强大的非线性映射、自适应和自主学习规则能力.其信息传递过程包括信号正向传播与误差反向传播.优异之处在于误差反向传播时，实现连接权值与阈值的更新，进而使输出层结果不断逼近理想期望值.由Kolmogorov定理可知：具有1层隐含层的3层神经网络能够在闭集以上以任意精度不断逼近n维至m维的非线性映射，n与m维分别代表输入、输出矩阵的维度，表明BP神经网络本质上为非线性映射函数.

1.2 遗传算法原理

遗传算法[9]是一种进化算法，其基本计算步骤如下：

1) 实现编码工作与种群初始化.将潜在最优解空间中的解数据表示为遗传空间基因型串结构数据，进而随机产生一定量的初始串结构数据，每个数据可单独看作种群中的一个个体，算法即从一定量的个体开始进行进化计算.

2) 进行种群个体适应度函数评估.适应度代表种群内个体优劣程度，根据生物学中“优胜劣汰，物竞天择”基本思想，采用轮盘赌法选择评估后适应度较高的个体，进行染色体的复制，使其下一代具备更高适应度.

3) 交叉与变异.利用步骤2中所选择的高适应度个体，按照一定比例进行两点交叉与变异，完成信息传递以及子代的生成，进而形成新种群，代表经过遗传算法后所模拟计算出的问题最优解空间.若不符合预设要求及精度，则返回至步骤2重新进行适应度函数评估.

1.3 主成分分析法

主成分分析法基本思想为将原输入矩阵通过坐标变换，在保留原有信息的基础上，映射至另外一组坐标系中，并非对原有特征变量进行简单删减，而是将若干新变量以原变量的线性组合重新代替原变量在信息传递中的表达.同时保留原有数据中对方差贡献量最大的特征来达到简化数据集的目的.新变量需满足以下：

1) 新变量需尽可能多地保留原变量所储存的相关信息；

2) 新变量之间需满足相互正交以消除原变量之间重复的信息；

3) 在实际数据分析应用中，往往选取贡献率总和为95.00%～96.00%的主成分作为矩阵变化后的新向量.

2 神经网络模型构建

2.1 数据预处理

2.1.1 模型数据及说明

此次数据来源于国内某电站机组连续运行5 d内传感器所收集机组实时监测数据，在机组连续运行过程中上机架、水车室以及蜗壳等多个部件出现较长时间异常噪声与振动现象，后经技术人员排查，发现机组转轮室中环钢板出现脱落，中环、下环出现严重裂纹，桨叶裙边损伤严重，检修后恢复正常运行.

机组额定功率200 MW，发电机型号为SF200-56/11950，立轴半伞式.传感器使用整周期采集模式，每4 096行数据为一个连续的数据波形并作为一个样本的数据长度，每256行为一个键相，每个波形共16个键相.采样频率为458 Hz.保证连续存储周期数是16,周期点数256点,时间分辨率精确至0.1 ms，根据传感器所测数据确定初始数据维度为50.

部分传感器测量部件与数据信息见表1，表中a1为x,y向摆度，d1为x,y向摆度间隙，γ1为x,y向摆度波形，A2为三相振动幅值，γ2为三相振动波形，d2为三相振动间隙，l2为三相振动偏移值，l3为x,y向振动偏移值，γ3为x,y向振动波形，T2为三相槽温度，p为压力，P有为有功功率，P无为无功功率，a0为导叶开度，n为机组转速，f为采样频率，l为样本长度.

表1 多传感器主要测量参数

其中1个采样周期内轴承波形数据与轴承摆度数据变化如图1所示.

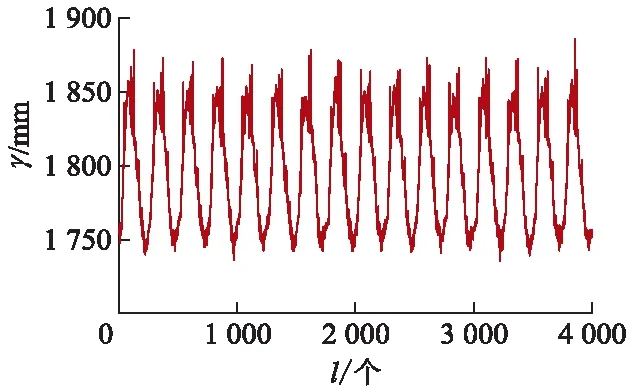
图1 1个采样周期内轴承波形变化示意图

从图1可看出，在1个样本周期内，波形数据波动范围为1个完整的波动周期，故在保证周期内样本数据完备性的基础上对1个采样周期内传感器数据取均值作为样本代表性数据.

BP神经网络作为有监督型神经网络，需要有输出数据以对仿真结果进行监督与参考，故将初始数据分为输入数据与输出数据.将多传感器在机组连续运行时间内所检测数据作为输入数据，其中正常运行数据与故障运行数据比值约为2∶1；将机组实际运行状态作为输出数据，正常运行与异常运行输出结果代码分别对应为1和2.

2.1.2 数据主成分分析

考虑到初始输入数据特征量繁多，为加快模型计算收敛速度、提高诊断准确率，对初始数据进行降维处理，具体步骤：

1) 将输入数据作为主成分分析输入矩阵，对其进行同一维度空间下线性转换，获得主成分系数矩阵、协方差矩阵等一系列变换矩阵；

2) 对输入矩阵进行去均值化操作；

3) 进行初始数据协方差矩阵贡献度分析，按照从小至大的顺序依次排列；

4) 确定贡献率累积在96.00%左右的主成分变量，并以此组成主成分变换矩；

5) 将主成分变换矩阵与取均值化处理后的输入矩阵进行相乘，即可获得贡献度累积在96%以上的特征变量经线性变化后的输入矩阵.

对协方差矩阵进行主成分分析后，得到的部分特征值、方差贡献率、累积贡献率见表2.

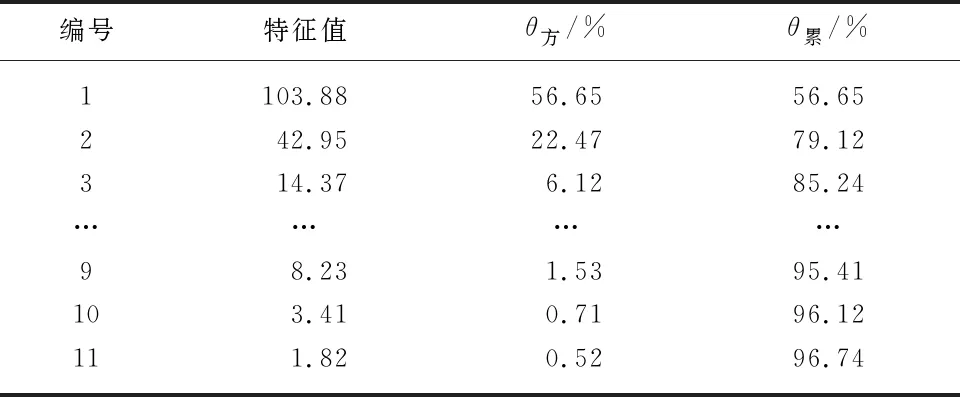
表2 主成分特征值与方差贡献率

由于主成分分析是在尽可能保留初始数据最大信息量的基础上对原有数据进行重新映射且线性组合，通过数据特征值以及方差贡献率来确定主成分，故无法确定所选主成分具体为何种传感器数据特征线性组合或是代表何种传感器数据.

由表2可知，前10个主成分已达96.12%的累积贡献率，对原始变量信息具备高水平的概括，且单个特征变量方差贡献率在编号为11时已跌至0.52%，参考意义不大，故选择前10个主成分作为初始数据经PCA降维处理后作为网络模型输入，输入层神经元个数取为10.

2.2 遗传算法优化BP神经网络

针对传统BP神经网络在训练中易出现局部极小值、收敛速度慢甚至不收敛的问题[10]，提出遗传算法全局寻优对神经网络进行优化，具体模型构建如图2所示.

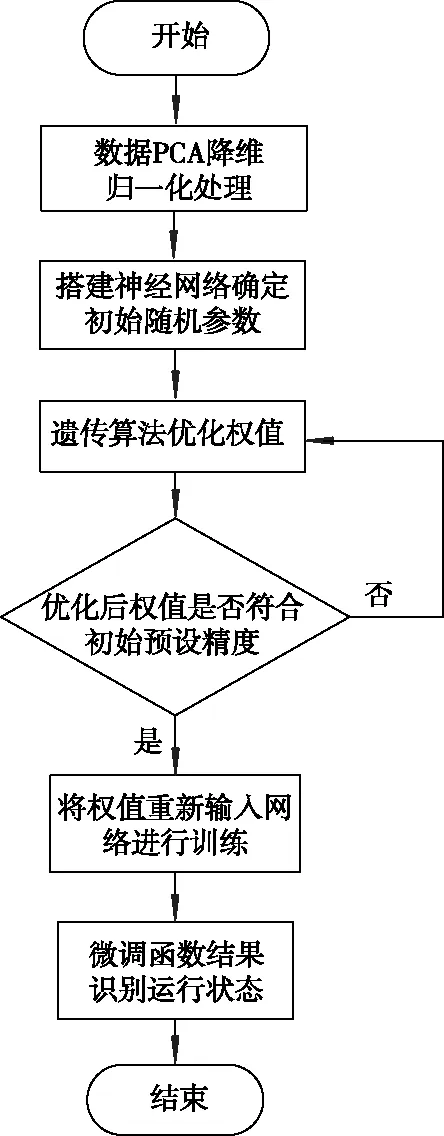
图2 网络模型构建示意图

具体优化步骤如下：

1) 将主成分分析后的数据作为网络模型输入.

2) 构建基础BP神经网络，由于数据间相差幅度过大，不利于数据深度挖掘以及模型训练计算，需对数据采用式(6)进行归一化处理，即

(6)

式中:下标max与min分别为x中对应的最大值与最小值.

3) 确立模型基本参数，其中隐含层神经元个数采用传统经验公式进行计算，即

S=2n+1，

(7)

式中：n为输入层神经元个数.

BP神经网络详细基本参数：神经元个数为11，传递函数Tansig，迭代次数2 000，误差精度0.000 01，训练学习率0.1.

4) 进行遗传算法优化，初始化种群，选择种群规模数为70，遗传代数为60代，进行选择、交叉、变异等操作以对BP神经网络连接权值与阈值进行全局寻优.

5) 将模拟后符合预设精度条件的参数重新输入基础BP神经网络进行模拟仿真，对仿真结果引入微调函数，使仿真结果逼近试验所设输出结果代码，以完成对机组运行状态识别.

3 试验结果与分析

将主成分分析后数据样本中正常、故障数据随机打乱排序，以前140组作为网络训练样本，后70组数据作为测试样本，通过训练样本训练网络模型，对训练完成的网络用测试样本进行测试，对比仿真状态与实际状态以统计状态识别正确率、状态检测时间.保证网络模型在大量数据下进行充分训练以提高异常状态识别结果准确度.

3.1 不同训练函数下试验结果分析

传统BP神经网络对模型参数存在较大敏感性，为探讨不同训练函数对PCA-GA-BP神经网络智能识别机组运行状态的影响，从提高模型鲁棒性以及可靠性的角度出发，选用不同训练函数对模型进行试验，试验独立进行，因神经网络自身缺陷问题易使结果值产生波动，故每组训练函数试验次数取为30次(每次试验重新对模型进行训练)，评估指标选为机组状态识别率与状态检测时间，参考结果均取平均值，如表3所示，表中θa为状态识别率，ta为状态检测时间.

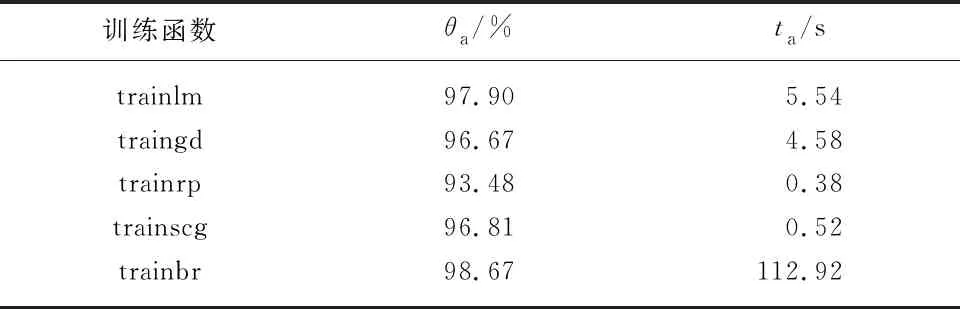
表3 不同训练函数对结果识别率以及识别效率的影响

从表3中可以看出，相较于传统BP神经网络所使用的梯度下降训练函数′traingd′，′trainbr′与′trainlm′训练函数在识别率上具有更明显的优势，识别正确率均在97.00%以上；在检测时间上，除去′trainbr′函数，其他函数检测时间均在6.00 s以内(检测时间与电脑配置有关，试验所用设备为Intel(R) Core(TM) i5-8400(2.80 GHz)，8 GB内存).但由于′trainbr′训练函数在训练时对内存需求较大，较其他训练函数所检测花费时间最多，且当样本数量增加时，检测时间过长会使时间成本增加，不符合对机组运行状态判别所需及时性、快速性的要求，反观′trainlm′训练函数，具备识别正确率高、识别速度快的特点，故对PCA-GA-BP网络模型选取′trainlm′作为训练函数.

3.2 综合分析

为充分验证基于遗传算法优化的BP神经网络在应用主成分分析法后相较于其他网络模型所具有的优势，引入PCA-BP,BP,GA-BP这3种网络模型进行对照试验，所选试验样本数据均一致，每组网络模型进行30次独立试验(每次试验重新对模型进行训练).同时，从增加模型状态识别精准度、提高模型识别时效性的角度出发，改变不同模型下训练样本与测试样本的比例，以增强数据结果可信度.状态识别率与检测时间均取平均值，3组对照试验所用训练函数均为′trainlm′.试验结果见表4.

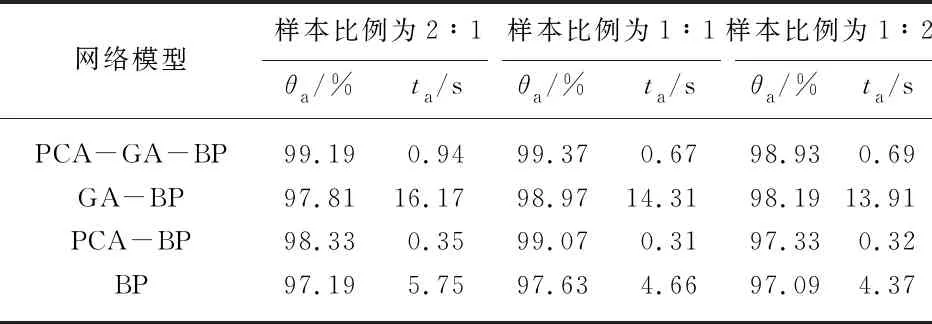
表4 不同网络模型不同样本比例下识别正确率与效率的对比

从表4中可以看出，基于主成分分析法的GA-BP网络模型，在3类不同样本比例的试验中，平均识别正确率最高，分别为99.19%,99.37%,98.93%；平均状态检测时间仅次于PCA-BP模型，分别为0.94，0.67，0.69 s.还可以发现，将遗传算法应用于网络模型后，对BP与PCA-BP网络模型，使其在基于93.00%～98.00%识别正确率的基础上进一步提升了0.50%～4.50%，导致这一现象可能是因为遗传算法通过全局寻优可获得符合预设精度的神经网络权值，在充分发挥传统神经网络广泛映射能力的基础上进一步提升模型精确度，有效提高状态识别正确率，且避免传统BP神经网络陷入局部极小值或收敛不全面的缺陷.将主成分分析法结合神经网络后，状态检测时间大幅度缩减，时间成本有效减少，对BP与GA-BP网络模型缩减幅度在93.00%～94.00%.经分析这是因为未经过降维处理的初始数据存在部分线性相关特征量，当样本数量较多时，会导致网络训练计算速度较低、收敛速度慢.且遗传算法对网络权值进行全局寻优时需要占用设备大量内存，故使得PCA-GA-BP网络模型在30次平均检测时间的结果表现上不如PCA-BP模型.

为更进一步说明文中所提PCA-GA-BP网络模型相较于传统BP网络模型的优势，将2种模型在3类样本比例下共90次试验中随机取出30 次试验识别率结果对比展示如图3所示.

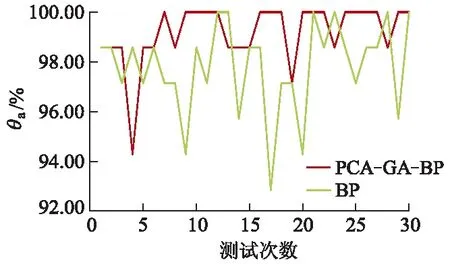
图3 2种网络模型识别正确率对比图

随机取出一次PCA-GA-BP网络模型试验测试样本预测结果对比如图4所示.

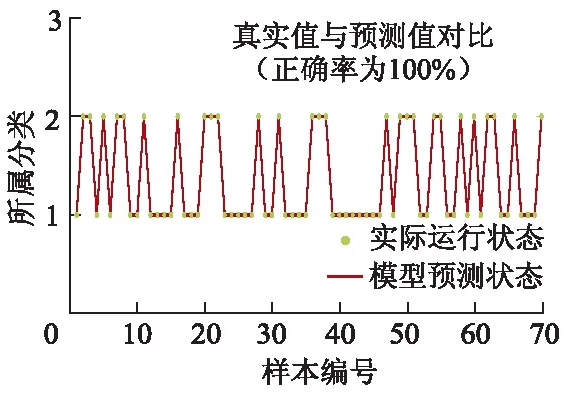
图4 PCA-GA-BP模型预测结果

观察分析可知：两类模型识别率众数区间均在92.00%～100.00%，且都出现范围不同的数值波动现象，经分析可能是因为神经网络自身缺陷以及遗传算法易寻求次优解所致.但根据30次试验整体表现，相对于传统BP神经网络，PCA-GA-BP在稳定性上具有更明显优势，具体表现为识别率波动范围小，低于6.00%，且模型稳定时间长，识别率众数较高，能对机组运行状态进行更为精确、稳定的预测，表明遗传算法能在一定程度上优化BP神经网络预测值的波动现象，结合图4中实际运行状态曲线与模型预测曲线100%的重合程度，验证文中所提网络模型在识别精度、识别效率以及模型鲁棒性上都有较为优异的表现.

4 结 论

文中提出一种将主成分分析法与遗传算法对传统BP神经网络进行优化的水电机组异常状态智能辨别方法.在充分发挥BP神经网络广泛映射能力与自主学习规则的基础上利用主成分分析法与遗传算法进行数据降维与网络阈值全局寻优处理，从而提高神经网络收敛速度和识别精度.结果表明，相较于其他网络模型，该方法运行状态检测时间下降至1.00 s以内，运行状态识别正确率均在98.00%以上，实现了更快速度、更高精度下对机器模型自主训练学习以对机组运行状态自我判别的作用，充分符合机组异常运行早期预警所需状态识别时效性与精确性，对机组实际运行具有重要工程参考意义.