重油裂化催化剂优化设计的动力学研究
2022-04-25戴薇薇李天伟李铁森
戴薇薇,李天伟,李铁森
(中国石油华东设计院有限公司,山东 青岛 266000)
催化剂具有高比表面积意味着其具有较多微孔,并具有多的活性位和高转化率,但此仅是理论假设。因为反应物分子首先需要进入催化剂内,并通过孔道扩散才能到达活性位。同样,产物也需要从活性位脱附,然后通过催化剂孔道扩散出去。绝大多数催化剂孔道小于1 nm,孔道虽然使催化剂表面积高,但反应物和产物分子在其中的扩散速率却较慢,如此将导致催化剂总活性受限。
事实上,在催化剂内部较深位置的活性位是很难或不能接近的,而且产物从活性位扩散至催化剂体相外的过程中可能会进一步反应,生成副产物[1]。
因此,催化剂内需要介孔或大孔孔道,从而作为“高速公路”使反应物接近活性位,而产物快速扩散至催化剂体相外。
重油分子的平均尺寸一般为3~5 nm,沥青质平均尺寸为4~12 nm[2],与催化剂孔道直径相当。因此,重油分子催化裂化反应主要受扩散控制[3]。
重油催化裂化催化剂中活性位分布对催化性能的影响至今尚不清楚。文中主要讨论催化裂化催化剂活性位表面分布(蛋壳型)和活性位均匀分布对催化性能的影响。
1 模型建立
假设蛋壳型和均匀型2 种类型催化剂中活性位数量相同,活性位体积为催化剂体积的1/3。因此,蛋壳型催化剂的壳层全部为活性位,而壳层内部为惰性基质;均匀型催化剂中活性位均匀分散于惰性基质中,但活性位浓度为蛋壳型催化剂壳层活性位浓度的1/3。
2种催化活性位的分布见图1。
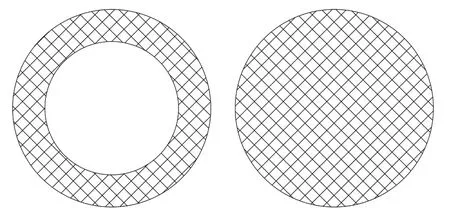
图1 FCC 催化剂活性位的分布:蛋壳型分布和均匀分布
根据反应物大分子在催化剂中扩散时的特点,对其扩散假设为:(1)扩散进入催化剂颗粒中大分子数量比总量少得多,因此催化剂外部反应物的浓度近似不变;(2)催化剂内部无主体流动。
2 重油催化裂化反应动力学
重油催化裂化过程是1 个众多组分高度耦合的复杂反应过程,为了简化反应动力学网络,常以集总的方式来描述该过程,即以少量具有代表性的虚拟组分来反应过程。文中采用Meng等[4]提出的8集总模型来表示重油催化裂化过程,该模型将催化裂化体系中所有组分划分为8个集总,见图2。

图2 8集总动力学模型
原料(集总1 和集总2)的速率方程由式(1)和(2)表示。

式中σ—与催化剂表面积碳相关的参数,其表示式见(3)。

式中 C/H—重油的碳氢原子比;T—反应温度;t—油气的停留时间;Rco—剂油比;Rso—蒸汽与重油的质量比;tc—催化剂的停留时间。
Meng等[4]获得的动力学数据见表。
根据表1 的数据,ki(i=13,14,…,18)可以表示为式(4)。

表1 8集总模型的指前因子与活化能

式中A—指前因子;Ea—表观活化能;R—摩尔气体常数,等于8.314 5 J/mol·K。
3 反应物在催化剂中的扩散与反应
设催化剂半径为R,r为催化剂球心到活性位微元的距离,则重油分子由外部扩散进入壳层微元的量Q1可由式(5)表示。
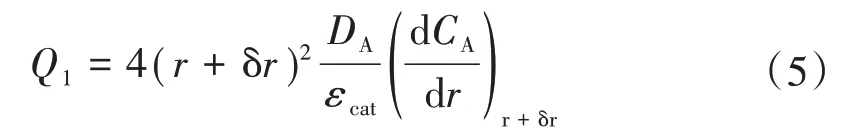
式中CA—反应物浓度,mol/gcat;DA—反应物分子的有效扩散因子,m2/s;εcat—催化剂的孔体积,m3/g。
反应物分子由壳层微元向球心扩散的量Q2可由式(6)表示。

反应物分子在壳层微元中的反应量Q3可由式(7)表示。

式中ρcat—催化剂密度,g/m3。
根据物料平衡,Q1-Q2=Q3,得到式(8)。
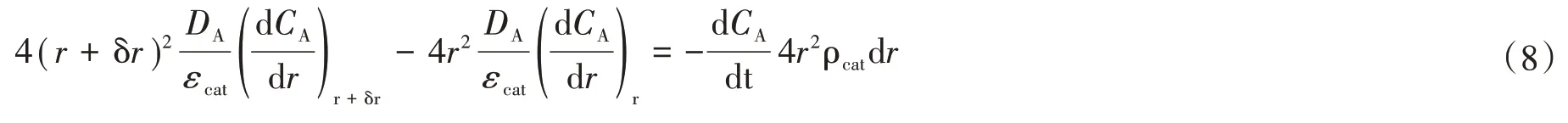
当δr→0时,式(8)可化简为式(9)。
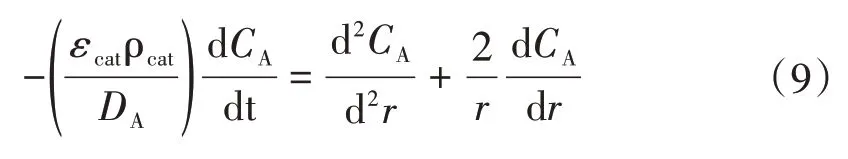
将式(1)代入式(9)可得式(10)。

引入无因次变量φ和λ,令

令球形颗粒的Thiele模数为
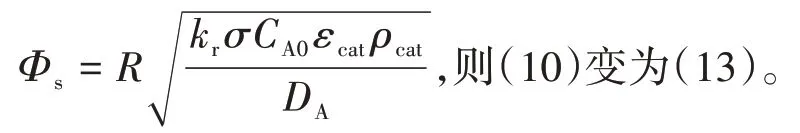

蛋壳型分布模型的初始条件和边界条件为:

均匀分布模型的初始条件和边界条件为:

以均匀分布模型为例,对13)采用有限差分法求 解 。 将 区 间[0,1]分 成N+1 等 份 ,步 长节点λ=ih(i=1,2,…,N)。在每个节点i上,用相应的2阶精度的中心差商近似导数代入方程(13)[5],得到式(16)、(17),(17)中,ui≈φi。

λ=0时,方程(13)根据L'Hôpital法则,有

因此,微分方程变为

其相应的差分方程为
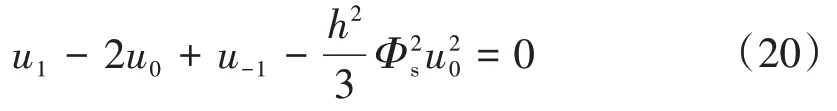

通过Newton-Raphson 法求解,将方程写成向量形式,有



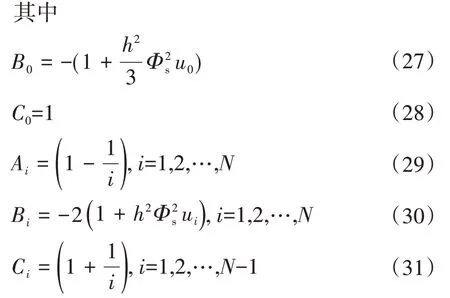
此模型中,取直径(R)为80 μm(常规直径为60~150 μm),密度为0.9 g/mL,孔体积为0.3 mL/g。
反应物以孤岛减压渣油为例,非芳香烃和芳香烃的分子量分别为710 和760,反应物非芳香烃和芳香烃的碳氢原子比(C/H)分别为0.52 和0.64;反应物有效扩散系数DA为10~12 m2/s[5~7]。反应温度为549.85 ℃,剂油比为16,蒸汽重油质量比为0.6,催化剂停留时间30 s,油气停留时间为3 s。
根据式(1)~(4)可得,活性位均匀分布时非芳香烃和芳香烃的反应动力学常数为25 111 g/mol·s和9 758 g/mol·s,σ分别为0.7和0.4。
根据以上条件即可获得重油中非芳香烃和芳香烃反应时的Thiele 模数分别为51.73 和32.24。当 N=40,Newton-Raphson 迭代精度为 10-10时,方程(13)的数值解见图3。同理,活性位蛋壳型分布时,方程(13)的数值解见图4。

图4 蛋壳型分布型催化剂中反应物无因次浓度分布

图3 均匀分布型催化剂中反应物无因次浓度分布
从图3、4 可见,催化裂化反应时,反应物来不及扩散到颗粒内,在外表面很薄的1层壳层内即被大量消耗,而催化剂颗粒内部的活性位很难被反应物分子触及。
4 催化剂内扩散有效因子
通常以有效因子大小表示扩散阻力和反应阻力相对大小,内扩散因子定义为式(32)。

对于重油催化裂化,反应的Thiele 模数较大,主要受扩散控制。因此,均匀分散型催化剂的有效因子η可表示为式(33)。



以方程(13)中Thiele 模数为变量,获得不同Thiele 模数下的值,代入式(34)或(36)从而求得有效因子η与Φs的关系,见图5。

图5 有效因子(η)随Thiele模数(ΦS)变化的关系
由图5 可知,相同Thiele 模数下,活性位蛋壳型分布的催化剂有效因子较高,即催化剂的活性位利用率较高。
当Thiele 模数为5 时,活性位蛋壳型分布型催化剂的活性位利用率为83%,而活性位均匀分布型催化剂的活性位利用率仅为40%。
当Thiele 模数较大时,催化剂有效因子与Thiele 模数的关系呈双曲线分布,活性位均匀分布型催化剂和活性位蛋壳型分布的催化剂满足以下关系:

对于重油催化裂化,反应物的Thiele 模数较大,因此蛋壳型催化剂中活性位的有效利用率相应较高。
5 结论
催化裂化过程中,分子筛催化剂进行选择性裂化,可将重油大分子裂化为高附加值的柴油、汽油等;而催化剂基质进行非选择性裂化,油品裂化生成大量干气和焦炭。对于常规催化剂,焦炭的生成量随催化剂中分子筛/基质比例增大而减少。为了增加高附加值产品的收率,提高催化剂的选择性,降低焦炭产率,开发分子筛为壳基质为核的蛋壳型催化剂结构更有利于重油大分子的裂化。
