二分类Logistic回归算法在化妆品功效评价中的应用
2022-04-25王福鑫矫筱蔓史延通
王福鑫 矫筱蔓 史延通

【摘要】 本文应用R语言对化妆品功效评价中产生的数据进行了基于二分类Logistic回归分析。使用逐步回归方法,发现数据自变量与因变量间的关系与差异,并建立Logistic回归模型,为今后化妆品功效试验设计参数的纳排方法提供重要参考。
【关键词】 R语言;化妆品功效评价;Logistic回归
【DOI编码】 10.3969/j.issn.1674-4977.2022.01.020
Application of Binary Logistic Regression Algorithm in Efficacy
Evaluation of Cosmetics
WANG Fu-xin,JIAO Xiao-man,SHI Yan-tong
(Liaoning Institute of Drug Control,Shenyang 110036,China)
Abstract: In this study,R language is used to analyze the data generated in the cosmetic efficacy evaluation based on binary logistic regression. Using stepwise regression method to uncover the relationships and the difference between independent variables and dependent variables. After that,the logistic regression model was established. The result will play an important role for the inclusion and exclusion methods of cosmetic efficacy evaluation experiment design in the future.
Key words: R language;cosmetic efficacy evaluation;logistic regression
在科学研究中,统计软件是必不可缺的实用工具。目前较为流行的统计分析软件是SPSS,然而SPSS功能有较大的局限性,可视化程度也较为简单。相较于SPSS软件,R语言以其开源、免费、多平台、体积小巧、编程简单、可视化等优点逐渐获得越来越多科研工作者的青睐。在化妆品功效评价研究中,R语言可帮助研究人员设计试验方案、进行数据分析和总结。化妆品功效评价研究常涉及众多目标参数的选择问题,确定参数间的相关性及差异性对指导后续试验研究工作尤为重要。以R语言为工具可较为直观且有针对性地对研究数据进行梳理分析,进而得到模型筛选后的目标参数。
以一种宣称具有抗衰老功效的化妆品原料为例,多项研究数据显示,该原料的功效效果存在差异,功效效果综合评价可选择有效或无效。为了今后企业开发设计是否添加该原料的化妆品,需要对该原料的多项实验中涉及的各项数据参数进行统计分析,发现哪些特征参数与功效效果有差异,哪些特征参数之间有相关性。
通过对上述研究内容的了解,二分类Logistic回归能很好实现研究的要求。二分类Logistic回归主要研究二元分类响应变量与诸多自变量之间的相互关系。
1 探索性分析
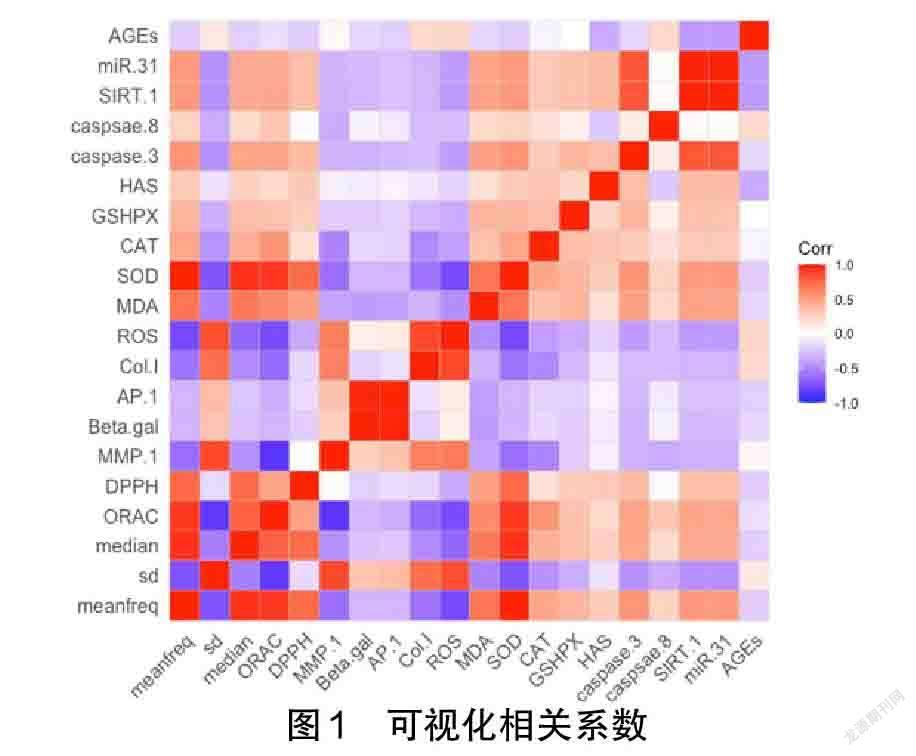
首先,因变量即不同效果用对应的数字表示,不能写成有效或无效,把有效和無效分别设置成0和1进行操作。研究的数据集包含1584个报告有效结果和1584个报告无效结果的数据样本(本研究所用数据和特征均为随机假设,非真实研究结果,仅为演示算法流程)。其中包含20个与皮肤抗衰老有关的特征参数,以其作为自变量。为了更好了解这20个特征参数之间的关系,可通过相关系数热力图可视化这20个特征参数之间的相关系数,程序和结果如下(下文数据分析均在R Studio环境下R语言版本4.1.1中进行):
> library(caret)
> library(ROCR)
> library(tidyr)
> library(corrplot)
> aging<-read.csv("/Desktop/Antiaging.csv",stringsAsFactors=F)
> aging_cor<-cor(voice[,1:20])
> ggcorrplot(aging_cor,method="square")
使用corrplot包中的corrplot.mixed()函数,可视化变量之间的相关系数。结果表明,很多特征之间的相关性很强,提示可能具有抗衰老机制的协同或拮抗作用。
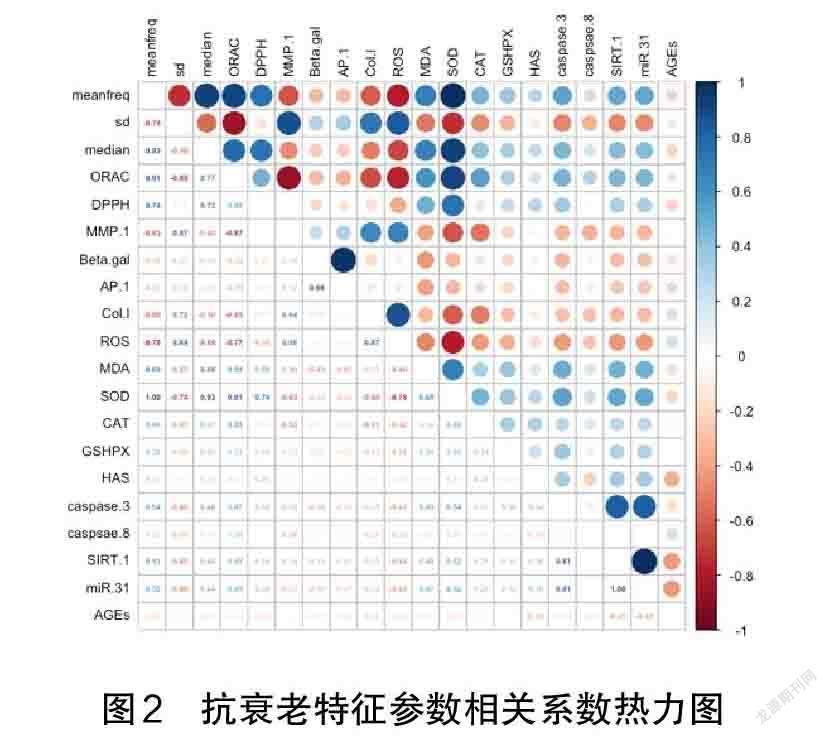
> corrplot.mixed(aging_cor,tl.col="black",tl.pos = "lt", tl.cex = 0.8,number.cex = 0.45)
通过图1、图2可以直观地显示20个特征参数之间的相关性,结果表明,很多特征之间有较强的相关性。接下来,使用可视化每个变量在不同功效结果下的密度曲线进行对比区分两种功效结果所有特征参数的差异,程序和结果如下:
> library(tidyr)
> plotdata<-gather(aging,key="variable",value="value",c(-label))
> ggplot(plotdata,aes(fill=label))
+theme_bw()+geom_density(aes(value),alpha=0.5)
+facet_wrap(~variable,scales="free")
通过图3可以发现,在某些特征参数下,抗衰老效果差异很明显,如CAT,Col-I,MMP-1,ORAC和sd等;有些差异则很不明显,如AGEs,DPPH,GSHPX等。
2 建立Logistic回归模型
在了解这些数据特征的关系和差异后,就可以建立Logistic回归模型对功效结果进行分类。建立Logistic回归模型可用glm()函数完成。为强化评估模型的泛化能力,使用数据集的70%作为训练集建立回归模型,使用剩余数据(30%数据集)作为测试集检验该模型的效果,程序和结果如下:
> aging$label<-factor(aging$label,levels=c("yes","no"),labels=c(0,1))
> library(caret)
> index <- createDataPartition(aging$label,p=0.7)
> agingtrain <- aging[index$Resample1,]
> agingtest <- aging[-index$Resample1,]
> aginglm <-glm(label~.,data=agingtrain,family="binomial")
> aginglmstep <- step(aginglm,direction="both")
> summary(aginglmstep)
## Call:
## glm(formula=label~median+MMP.1+AP.1+Col.I+ROS+MDA+
## CAT+GSHPX+AGEs,family="binomial",data=agingtrain)
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -4.5356 -0.0935 -0.0002 0.0277 3.2539
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 16.264823 8.964575 1.814 0.06962 .
## median 10.819219 5.793547 1.867 0.06184.
## MMP.1 ; -59.369107 5.833076-10.178<2e-16 ***
## AP.1 0.003397 0.001373 2.475 0.01332 *
## Col.I -46.684861 10.689227 -4.367 1.26e-05 ***
## ROS 12.690259 2.347499 5.406 6.45e-08 ***
## MDA -3.807964 2.610757 -1.459 0.14468
## CAT 181.523806 11.689991 15.528 < 2e-16 ***
## GSHPX -44.233663 10.262250 -4.310 1.63e-05 ***
## AGEs 4.452719 1.533414 2.904 0.00369 **
## ---
## Signif.codes:0‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## (Dispersion parameter for binomial family taken to be 1)
## Null deviance:3074.80 on 2217 degrees of freedom
## Residual deviance:347.82 on 2208 degrees of freedom
## AIC:367.82
以上程序使用step()函數进行了逐步回归分析,以该方法可以从20个特征中选择显著的特征建立模型。在建立回归模型后,通过指定的glm()中的参数family进行Logistic回归。
结果发现,模型的AIC=368.82,且模型只用了9个变量(median、MMP-1、AP-1、Col-I、ROS、MDA、CAT、GSHPX、AGEs)作为回归模型的自变量,并且每个变量都是显著的,可剔除掉其余11个不显著的自变量。结果说明,这9个特征参数的变化对该原料抗衰老功效效果有显著影响,可在今后研究中着重研究这9种特征。
3 逐步逻辑变量筛选过程
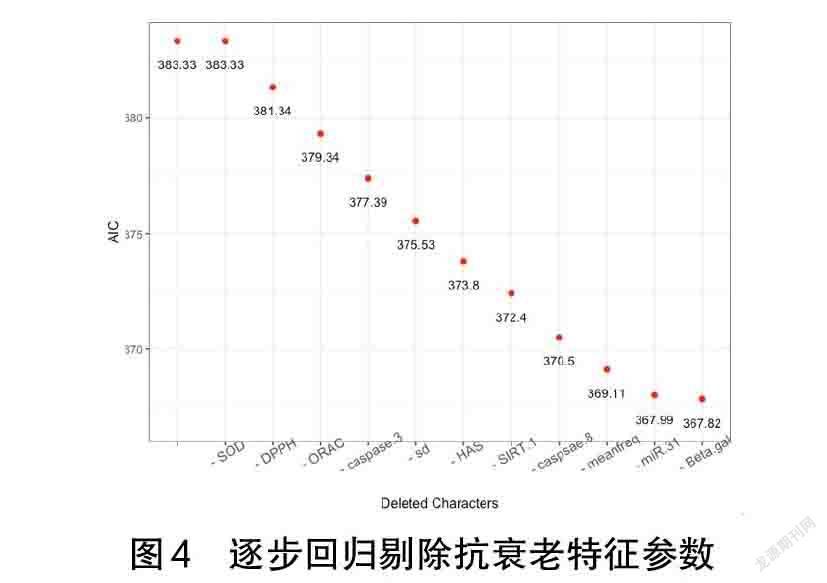
在优化Logistic回归模型中,采用逐步回归剔除不需要的自变量。利用R可视化逐步回归(见图4),观察过程中AIC值的变化情况,可更直观地显示优化状态。程序和结果如下:
stepanova<-aginglmstep$anova
stepanova$Step<-as.factor(stepanova$Step)
ggplot(stepanova,aes(x=reorder(Step,-AIC),y=AIC))
+theme_bw(base_size=12)
+geom_point(colour="red",size=2)
+geom_text(aes(y=AIC-1,label=round(AIC,2)))
+theme(axis.text.x=element_text(angle=30,size=12))
+labs(x="Deleted Characters")
在剔除过程中,AIC值一直在减小,模型的稳定性逐漸增强。例如:剔除SOD这个参数后,AIC值没有变化。这是因为SOD这个特征参数在原始模型中是使模型奇异的特征,可以由其他特征的线性组合代替。这样的特征参数存在只会对模型产生不稳定性。
由于Logistic回归主要针对二元分类响应变量,所以也可用于设置有无某些功效,并把诸多检测参数引入,建立回归模型判定哪些指标对该功效影响显著,进而作为功效评价研究纳排指标的重要参考依据。
【参考文献】
[1] 许汝福.Logistic回归变量筛选及回归方法选择实例分析[J].Chin J Evid-based Med,2016,16(11):1360-1364.
[2] 刘二钢,马建强.R语言在统计分析中的使用技巧[J].Computer Knowledge and Technology,2017,13(1):251-256.
[3] 张婷婷.Logistic回归及其相关方法在个人信用评分中的应用[D].太原:太原理工大学,2017.
【作者简介】
王福鑫,男,1984年出生,主管药师,博士,研究方向为化妆品功效安全评价。
矫筱蔓,女,1978年出生,主任药师,硕士,研究方向为化妆品检验技术。
史延通,男,1975年出生,研究员,硕士,研究方向为化妆品监管。
