“具身认知”视野下的小学数学实验教学

庄曾曾

[摘  要] 数学实验是数学学习的重要组成。在“具身认知”视野下，数学实验教学能有效地提升学生的学习力，发展他们的数学学科核心素养。如何开展数学实验是文章主要探讨的内容：研发“实验内容”，让数学实验从零散走向统整;优化“学习方式”，让数学实验从外促走向建构;促进“学习互动”，让数学实验从单向走向多维。

[关键词] 小学数学;具身认知;实验教学

数学实验是一种兼具演绎性和归纳性、理论性和实验性的学习方式。在“具身认知”视野下，数学实验教学能有效地提升学生的学习力，发展学生的数学学科核心素养。对于学生来说，数学实验不仅仅是学习的一种手段、方法，更是数学学习的重要组成。学生需要认识、理解、操作、反思数学实验等。在实验的过程中，教师要激发学生的实验动机，精准开发实验内容、引导学生展开积极的实验互动。在整个数学实验的过程中，教师要引导学生多感官协同活动，让学生的实验过程成为一种全身心感受、体验的过程。在数学实验中，学生积累了丰富的数学基本活动经验，感悟到相关的数学思想方法。

[⇩] 一、研发“实验内容”，让数学实验从零散走向统整

当下的数学实验，存在着一些问题。其中，最为明显的一个问题就是数学实验内容的零散化、随意化。很多数学实验，往往是附属于某些数学知识而探索的，缺乏独立存在的依据。师生的数学实验往往有着一种“脚踩西瓜皮，滑到哪里是哪里”倾向。今天这一个数学知识点，想实验就实验，不想实验就不实验。研发“实验内容”，就是要让数学实验从零散走向统整、从粗放走向集约。

相较于过去零散型、粗放型的数学实验，具有统整性、结构性、系统性的数学实验，其实验目的更明确，实验内容更精细，实验方式更精准。实验不是随意的，而是有计划、有目的、有组织的。数学实验的功能，也不仅仅停留在操作的层面上，而是包括数学思维、想象在内的综合考量。在实验立意上，教师要高点定位;在实验内容上，教师要有效聚焦;在实验方式上，教师要引导学生深度建构。比如教学“多边形的面积”时，教师在备课中就要清楚知道每一个知识点需要展开的数学实验，同时要引导学生把握数学实验的内在关联。在对教材中的平行四边形、三角形以及梯形的面積推导过程进行深入研究之后，我们建构了序列化、结构化的实验内容。具体而言，就是引导学生应用“剪拼”实验方法推导“平行四边形的面积”;用“剪拼”“倍拼”实验方法推导“三角形的面积”;用“剪拼”“倍拼”“分割”实验方法推导“梯形的面积”。显然，这一部分实验内容以及实验方式各具特色。教师通过对这一部分内容的实验教学，不仅能让学生经历“平行四边形的面积”“三角形的面积”“梯形的面积”的推导过程，让学生掌握了相关知识，更为重要的是，让学生形成了系列性的操作技能，积累了丰富的操作经验。同时能让学生感受、体验到数学的转化思想，即新知转化为旧知、复杂转化为简单、陌生转化为熟悉。

研发实验内容，就是要杜绝实验设计、规划的随意性和无目的性，就是要让学生的数学实验成为数学学习的重要组成。在教学中，教师不仅要研究相关的实验内容，更要研究学生的具体学情，从而能让学生的数学实验具有科学性、合理性、适切性。

[⇩] 二、优化“学习方式”，让数学实验从外促走向建构

传统的数学实验，往往是教师要求学生做的实验。实验内容由教师决定，实验方式由教师规定，实验目标由教师厘定，这样的实验是一种“被动实验”。如何让学生做实验从被动走向主动、从浅层走向深层？笔者认为，最为重要的就是要优化学生的数学学习方式，进而让学生的数学实验从外促走向建构。建构性的数学实验是一种积极的、主动的数学实验，是能有效地提升学生学习力、发展学生数学核心素养的实验。

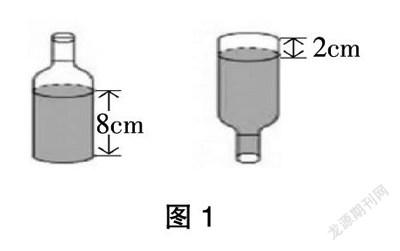
优化数学实验方式，能激活学生的“实验之情”，能引发学生的“实验之意”，能催生学生的“实验之志”。在实验的过程中，要关注学生的情感、学习的氛围等。比如教学“圆柱和圆锥”时，学生遇到了这样的问题：一个玻璃瓶的内直径是6厘米，如果在里面装入8厘米高的水，然后将瓶子倒过来，空余部分的高是2厘米。这个玻璃瓶的容积是多少毫升？（见图1）

很多学生在思考问题时，都不同程度地受到了玻璃瓶不规则的上端容积的影响，固化的思维钳制着学生，让学生难以形成正确的解决问题的思路，难以将左右两幅图联系起来思考。为此，笔者特地找来了一个玻璃瓶，让学生动手做“演示实验”。在学生操作实验的过程中，笔者启迪学生思考：将玻璃瓶正反放置，什么有变化，什么没有变化？这样的提示，让学生在观摩实验时，不再仅仅感受到“好玩”，更为重要的是引发他们对玻璃瓶容积、水的体积等深度思考。学生发现，不管怎样放置玻璃瓶，有两个量是不会发生变化的：一是玻璃瓶的容积（体积）;二是玻璃瓶中水的体积。同时，有学生还发现，尽管玻璃瓶中注入的水在颠来倒去之后，形态发生了变化，瓶中空置部分的形态也发生了变化，但空置部分的体积总量没有发生变化。根据这样的实验操作和推理，学生能有效地突破玻璃瓶不规则的认知难点，从而找到相关的数量关系。借助这样的数量关系，学生有效地解决了之前提出的问题。在这个过程中，学生把握了“变与不变”的关系，对“量的恒定思想”等相关内容也有了更深层次的理解。

优化学生的数学学习方式，不仅要关注实验的工具、内容、操作及对相关知识的探究和理解，更要关注实验过程中师生在心理、情感等方面的表现。在小学数学实验教学中，教师要有效地建构实验情境，从而将学生引入情境，以情激智，以智生情，进而让学生的数学学习情智交融。通过数学实验，培养学生的理性品质，锤炼他们的理性精神。

[⇩] 三、促进“学习互动”，让数学实验从单向走向多维

数学实验不仅是学生个体的活动，而且是学生群体的活动。在实验过程中，教师要引导学生进行实验互动，让学生的数学实验从单向走向多维。从某种意义上说，数学实验就是教师、学生之间通过实验文本，利用实验器具进行活动的过程。在这个过程中，各个主体之间要相互协商、合作，要畅快地表达自己的实验见解、主张等。实验性的活动能引发学生相互吸纳、相互滋养，从而促进学生达成共识，推动学生的全面发展。

比如教学“圆的面积”时，传统的数学实验教学往往是遵循教材的要求，仅引导学生将圆转化成近似的长方形。至于“为什么这样转化”等相关的问题，学生在实验中没有触及。笔者在教学中大胆地放权、赋权，让学生展开自主性、自能性的数学思考与探究。在学生进行实验探究之前，笔者首先和学生一起复习了相关的平行四边形面积、三角形面积以及梯形面积的推导过程。通过回顾这些图形面积的推导过程，来启发、引导学生积极的数学猜想和验证。在分组探究的过程中，不同的小组形成了不同的探究方案。如有小组学生将圆分割拼接成近似的长方形;有小组学生将圆分割拼接成近似的三角形;还有小组学生将圆分割拼接成近似的梯形等。在积极的互动中，学生能有效地进行对比，进而发现“圆的面积”这一数学实验的共性，都是将曲线图形转化成直线图形，都是将未知的、复杂的、陌生的图形转化成已知的、简单的、熟悉的图形。在这个过程中，学生能感受、体验到化曲为直的数学思想，感受、体验到极限思想，感受、体验到转化与化归的数学思想和方法。学生在数学实验中体验、互动，从而促进其对圆的面积公式的推导以及对整体性意义的理解和把握。

数学家欧拉认为，学习数学这门学科，不仅需要观察，而且需要实验。“具身认知”视野下的数学实验教学，要激发学生的实验兴趣，调动学生的实验积极性。在实验过程中，要根据数学知识的特点以及学生的具体学情，从实验的内容、实验的驱动力以及实验的方式、实验的互动等方面进行综合性考量。通过数学具身性的实验，集聚学生的数学学习感受、体验，促进学生对相关数学知识的理解、把握，从而不断地提升学生的数学学习力、实践力，发展学生的数学核心素养、综合素养等。