地铁钢弹簧浮置板阻尼参数试验及其对行车的影响研究
2022-04-24程曜彦方宏凯李新国
程曜彦,方宏凯,李新国
(同济大学教育部道路与交通工程重点试验室,上海 201804)
钢弹簧浮置板轨道自1977年由Grootenhuis[1]首先提出并成功应用于德国科隆地铁,作为目前在城市轨道交通减振降噪研究领域应用最为广泛、效果最受认可的减振结构,一直是该领域研究的热点。钢弹簧浮置板减振轨道结构由一定质量、刚度的混凝土道床板和钢弹簧组成的质量-弹簧减振系统,相比于其他轨道减振型式具有固有频率低、减振效果良好的特点,试验和研究表明其减振效果可达20~30 dB[2]。
在钢弹簧浮置板的减振性能研究方面,国内外学者相关研究成果如下:Cui等[3]采用无限长Timoshenko梁模拟钢轨,结果表明浮置板轨道对频率高于 15 Hz的振动衰减作用明显;吴天行[4]、李增光等[5]和王炯等[6]在频域内建立了车辆-轨道结构系统的数值计算模型,对比了浮置板轨道的减振、隔振性能;吴磊[7]在提出地铁车辆-钢弹簧浮置板轨道动力学耦合模型及其数值计算程序的基础上,较为全面地研究了钢弹簧浮置板减振降噪性能。
钢弹簧浮置板道床对于小于20 Hz的低频段尤其是结构固有频率附近频段,其减振效果较差甚至产生振动放大效应,这些低频振动对于一些高精密仪器和生产设备的正常工作具有很大的影响。研究发现,在刚度不发生改变的情况下,适当增加阻尼耗能可以有效地减小结构低频段的振动[8-10]。钢弹簧隔振器的阻尼是影响浮置板轨道减振效果的关键参数,因此,选择合适的测试方法及传感器参量来准确测试钢弹簧阻尼隔振器组件阻尼,是明确浮置板轨道减振效果的前提,也可用来验证产品是否满足设计要求[11-14]。在轨道结构减振系统中添加阻尼,可以抑制系统振幅,使列车通过浮置板时较为平顺,但阻尼过高会降低系统的减振效率,同时,阻尼比的测试也是轨道动态性能测试的一个必测项目[15-19]。因此,阻尼相关参数的选择对于列车平稳运行及环境振动有着重要影响。
综上所述,钢弹簧浮置板轨道结构的阻尼设置在振动传递中作用关键。尽管针对这方面的研究已经成为近年来最热门的问题之一,但是目前对于钢弹簧浮置板隔振器的阻尼取值方面的研究仍然不够成熟。结合钢弹簧隔振器阻尼锤击试验及车辆-轨道-桥梁系统耦合数值分析两种方法,分析了钢弹簧隔振器阻尼参数设置对钢弹簧浮置板轨道系统动力响应及地铁车辆行车平稳性、安全性的影响。
1 钢弹簧隔振器阻尼比测试
1.1 测试原理
钢弹簧浮置板减振轨道结构是将一定质量和刚度的混凝土道床板浮置于由钢弹簧和钢套筒组成的隔振器上构成质量-弹簧-隔振系统,其主要由基底、浮置板、隔振器、轨枕、扣件以及钢轨等组成,可有效隔振、减振。如图1所示。

图1 钢弹簧浮置板结构横断面
隔振效果通常用隔振系数η和隔振效率E来衡量,计算方法如式(1)所示。

(1)
式中,ξ为阻尼比;λ为激振频率与固有频率之比。
钢弹簧隔振器阻尼比的测试原理为将一钢弹簧隔振器放置于水平地面上,在隔振器正上方居中放置质量为m的混凝土质量块,组成等效的单自由度质量-弹簧-阻尼系统。如图2所示。

图2 钢弹簧隔振器阻尼比测试原理(单位:mm)
该系统的自由振动方程,如式(2)所示。

(2)
式中:m为质量块的质量;c为阻尼器的阻尼系数;k为钢弹簧刚度。
考虑到测试系统为小阻尼体系,令u(t)=est,并将其代入式(1),得到式(3)~式(6)。

(3)

(4)
c=2mωnξ
(5)

(6)
则任意两个相邻振动峰值之比,如式(7)所示。

(7)
由式(7)可知,钢弹簧隔振器相邻振动峰值之比仅与阻尼比有关,与i无关。
式中,λ为对数衰减率,表示相邻振动峰值比的自然对数值;由于该系统为小阻尼体系,为获得更高精度的测试结果,可采用相隔n个周期的振动峰值比来计算其阻尼比。
相隔n个周期对数衰减率λ和阻尼比ξ,如式(8)所示。
(8)
其中,λ为单个波形的对数衰减率;n为自由振动波形个数;ui为第i个波峰幅值;ui+n为第i+n个波峰幅值。
1.2 测试方案
钢弹簧隔振器阻尼比测试系统主要由1.2 t混凝土质量块、891-2型拾振器(传感器)、891型六线放大器及DH5920动态信号测试分析系统组成。如图3所示。

图3 钢弹簧隔振器阻尼比测试系统
根据钢弹簧隔振器实际受力时的状态,测试选取质量为1.2 t的混凝土质量块,置于隔振器正上方;质量块离开地面一定高度,以保证在锤击的过程中质量块不会因接触地面而影响测试结果;质量块上表面中心处放置一块铁垫板,即锤击力的施加位置;为保证测试精度,在靠近质量块中心位置对称放置4个相同的传感器,数据处理时取4个传感器的测试数据的平均值作为测试结果。
在锤击力施加位置对混凝土质量块m分别施加4档不同大小的锤击力,当被测试系统激振时,在传感器上获取加速度、速度、位移对应测试数据,同时统计出4档锤击力锤击时传感器得到的测试数据分别对应的加速度、速度、位移指标大小范围,作为区分4档锤击力大小的控制范围,如表1所示。为消除测试时随机误差,先设置1组平行试验。

表1 4档锤击力条件下传感器产生的测试指标范围
1.3 测试数据的处理与分析
为提高测试数据精度,须消除由于质量块在各种模态振动、环境振动等产生干扰的信号,因此,将4个传感器通道得到的原始数据导入MATLAB,并通过巴特沃斯滤波方法,滤除试验系统固有频率±20%范围以外的频率,以得到较平顺的波形。固有频率计算公式为

(9)
已知测试系统的静刚度k=5.606 N/mm;试件的质量m=1.2 t;计算ωn=10.88 Hz,滤波之后留下的是频率在8.704~13.056 Hz之间的曲线部分。
经由Matlab软件编制的滤波函数程序处理后,得到可进行计算的数据图像并舍弃第一个峰值,从第二个峰值开始计算,并代入到理论计算部分中的阻尼比计算公式(8)中,即可得到阻尼比实测值。按照测试方案中施加4档锤击力锤击质量块产生垂向振动时测得加速度、速度、位移的各10组有效数据。选择自由衰减振动波形中的峰值间隔周期n=1~5进行计算,得到阻尼比数据经MATLAB程序处理结果。如表2所示。

表2 4档锤击力加载测得的阻尼比平均值计算结果
(1)通过选取传感器的测试参量为加速度、速度、位移时测试得到的阻尼比平均值对比,可知1档时的误差百分比分别为9.138%,2.131%和5.30%,误差较大,略去;2档~4档时的误差百分比分别为1.0%~2.8%,1.1%~3.9%,1.5%~2.3%。因此,锤击力在2档~4档内,锤击力大小对测试结果的影响较小。
(2)通过对比传感器测试参量分别为加速度、速度、位移时测试得到的阻尼比平均值得到的误差百分比,n=1,n=2和n=5时的误差百分比分别为13%~22%、8%~18%、2%~8%,误差较大,略去。自由衰减振动波形中峰值间隔周期n=3,n=4时,在选择加速度、速度、位移为测试参量时测得阻尼比最大误差分别为0.2%,1.6%,2.4%,误差较小、参数选择合适。
(3)分别采用自由衰减振动波形中峰值间隔周期n=1~5,来计算选用测试参量为加速度、速度、位移的传感器测试得到的阻尼比与n的关系如图4所示。

图4 测试参数为传感器测试得到的阻尼比与n的关系
由传感器的加速度、速度、位移参量测试得到的阻尼比与选择不同n时计算得到对应阻尼比均值的误差百分比如图5所示。

图5 加速度、速度、位移传感器测试得到的阻尼比与选择不同n时计算时得到对应的阻尼比均值的误差百分比
由图4与图5可知,采用加速度、速度、位移传感器上得到的阻尼比三者之间的关联性随着n值的增加较好,尤其是在n=3、n=4时,3种参数的传感器阻尼比最大相差0.003,阻尼比最大误差百分比在3%以下。
2 钢弹簧阻尼对桥上浮置板轨道结构振动传递特性分析
2.1 钢弹簧浮置板-箱梁桥结构模型
桥上浮置板轨道结构模型中钢轨采用CHN60钢轨,弹性模量2.1×1011N/m2,密度7.85×103kg/m3,泊松比0.3,钢轨横截面积7.7×10-3m2;扣件刚度1.0×107N/m,阻尼5.0×104N·s/m,扣件间距0.6 m;浮置板密度为3 000 kg/m3,弹性模量为3.45×1010N/m2,泊松比为0.17,尺寸为31.8 m×3.4 m×0.3 m;钢弹簧刚度为6×106N/m,阻尼为1×104N·s/m,钢弹簧间距为1.5 m;桥梁结构为单跨32 m箱梁,梁体密度为3 000 kg/m3,弹性模量为3.35×1010N/m2,泊松比为0.167;桥墩刚度为3×109N/m,阻尼为1×105N·s/m。如图6所示。
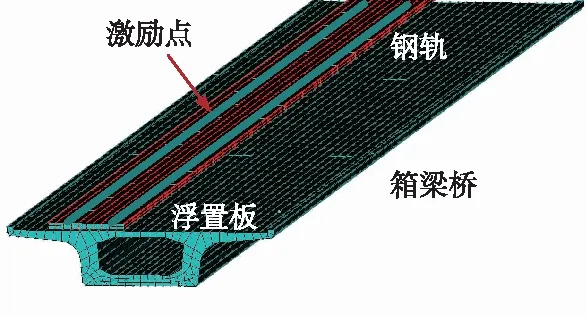
图6 钢弹簧浮置板-箱梁桥结构模型
数值计算软件采用ANSYS软件,其中采用欧拉梁模拟钢轨单元,弹簧单元模拟扣件,实体单元模拟浮置板,钢弹簧采用弹簧单元模拟,实体单元模拟桥梁。
2.2 钢弹簧阻尼对桥上浮置板轨道结构振动传递特性分析
钢轨、浮置板以及桥梁的位移导纳和桥墩传递的力导纳可作为轮轨作用力向下的传递特征[19-22]分析钢弹簧阻尼浮置板轨道结构振动传递特性。本节计算了浮置板轨道结构的钢弹簧阻尼分别为10,30,50 kN·s/m条件下1~500 Hz频段内车辆动荷载作用点正下方的钢轨位移、浮置板位移、桥梁位移以及桥墩传递下的作用力变化情况,不同阻尼作用下的轨道结构的动力响应。如图7所示。

图7 3种钢弹簧阻尼作用下轨道结构振动传递特性
简谐激励为3 Hz时对应的由桥梁共振引起响应幅值及轨道结构的第一共振频率(8 Hz)对应的响应幅值如表3所示。

表3 3种钢弹簧阻尼作用下的振动传递特征幅值
如图7、表3所示,在简谐激振1~500 Hz时,在钢弹簧阻尼分别为10,30,50 kN·s/m时,浮置板垂向位移导纳在第一共振峰处的幅值分别为11.60×10-8,6.43×10-8m和4.40×10-8m,表明轨道结构在第一共振峰处的振动响应随着钢弹簧阻尼的增大显著减小。
3 钢弹簧阻尼参数对行车影响分析
3.1 车辆-轨道-桥梁动力耦合模型
车辆-轨道-桥梁动力相互作用系统主要由车辆、轨道、桥梁3个子系统构成,子系统之间通过轮-轨关系、桥-轨关系进行系统耦合,是典型的复杂空间耦合时变系统,如图8所示。为建立车辆-轨道-桥梁系统仿真模型,在分析了浮置板轨道-简支箱梁桥振动特性基础上,利用SIMPACK与ANSYS联合仿真。

图8 车辆-轨道-桥梁耦合模型
地铁车辆多体动力学模型在SIMPACK中搭建,车辆类型为B型;轨道和桥梁子结构分析在ANSYS中完成。假设轨-梁-墩为柔性系统,生成所需要的*.cdb和*.sub文件,再将作为柔性体的结构模型导入SIMPACK,各部件通过非线性弹簧阻尼力元连接。由于多体动力学软件中几何外形不参与动力学计算,可在SIMPACK中直接调用默认车体几何外形。钢轨建模参考CN-60型参数,且只考虑桥梁段上的轨道为柔性体结构。之后通过*.fbi文件及编写包含轨道信息的*.ftr文件来搭建柔性轨道,并实现轮轨间数据交互。
计算条件:车速为60 km/h及80 km/h;浮置板钢弹簧阻尼为10~70 kN·s/m;计算时列车单线靠左侧匀速通过桥梁区段。
3.2 钢弹簧阻尼对地铁车辆动力响应影响分析
不同钢弹簧阻尼及行车速度条件下对地铁车辆动力响应的影响,如图9所示。

图9 钢弹簧阻尼及行车速度对车辆动力响应的影响
在车辆速度分别为60 km/h和80 km/h条件下,改变钢弹簧阻尼对车辆行车平稳性及安全性评价指标的影响规律大体一致,各指标值均随阻尼的增大而减小、随行车速度的提高而增大。
(1)依据车辆平稳性指标随钢弹簧阻尼及行车速度变化情况,在行车速度一定的情况下,各指标值均随着钢弹簧阻尼增加而减小:在行车速度为60 km/h时,车体横向加速度和垂向加速度分别由0.031g减小为0.029g、0.069g减小为0.021g,横向平稳性和垂向平稳性则分别由1.755减小为1.591,由2.255减小为1.643。由此说明,增加钢弹簧阻尼可提高旅客乘坐舒适度,但是当钢弹簧阻尼大于50 kN·s/m时,各平稳性指标的变化幅度相差很小。这是由于钢弹簧阻尼是由具有强烈非线性阻尼特性(迟滞特性)的橡胶、聚合体等弹性元件提供,橡胶的阻尼随着阻尼的增加,只对高频振动的传递率稍有影响。车辆平稳性指标计算时,对于车辆地板振动加速度大于20 Hz时计权系数取为1,说明大于20 Hz的振动对于车辆平稳性影响较小。因此,当钢弹簧阻尼高于某个值(50 kN·s/m)时,平稳性指标变化较小。
(2)依据车辆安全性指标随钢弹簧阻尼及行车速度变化情况,在行车速度一定的情况下,车辆安全性指标均随着钢弹簧阻尼增加而减小:以相对不利的行车速度即80 km/h为例,增大钢弹簧阻尼,轮轨垂向力逐渐减小,最大为53.2 kN,远小于170 kN的安全限值,在钢弹簧阻尼大于50 kN·s/m后轮轨垂向力基本保持不变;车辆脱轨系数随着钢弹簧阻尼的增加而减小,在钢弹簧阻尼大于50 kN·s/m时,脱轨系数在0.2附近变化不大,表明此时钢弹簧阻尼的变化对车辆脱轨系数的影响已不明显。这是由于轮轨相互力包含高频P1力和准静态P2力,用于脱轨系数计算时的车轮施以钢轨的横向作用力Q和车轮作用于钢轨的垂向作用力P为准静态力,而钢弹簧阻尼隔振器的阻尼增加时,由于橡胶阻尼特性只对高频振动传递率稍有影响,当钢弹簧阻尼大于某个值(50 kN·s/m)时,阻尼对车辆脱轨系统影响不明显。
4 结论
结合钢弹簧隔振器阻尼锤击试验及车辆-轨道-桥梁耦合数值计算两种方法,分析了钢弹簧隔振器阻尼参数对钢弹簧浮置板轨道系统动力响应及行车平稳性的影响,得到了钢弹簧浮置板轨道振动传递特性及阻尼参数对地铁车辆行车的影响,结论如下。
(1)根据钢弹簧隔振器阻尼比测试室内试验数据,可选取测得加速度、速度、位移数据来计算钢弹簧隔振器阻尼比;钢弹簧隔振器阻尼参数试验表明,锤击力在2档至4档是锤击力选择的合适范围;当n取值为3和4时阻尼比计算结果相差不大,在计算自由衰减振动的钢弹簧阻尼比时,波形峰值间隔周期n值合适的选择为3和4;在锤击法测试钢弹簧隔振器阻尼比试验中,选用加速度、速度、位移作为测试参量,计算得到的钢弹簧隔振器阻尼比结果最大误差在3%以内,表明选取传感器3种测试参量阻尼比测试结果基本一致,均可作为测试指标值。
(2)钢弹簧阻尼变化对轨道结构振动传递特性的影响分析表明,在简谐激振 1~500 Hz内时,轨道结构在第一共振峰处的振动响应随着钢弹簧阻尼的增大而显著减小:在钢弹簧阻尼分别为10,30,50 kN·s/m时,浮置板垂向位移导纳在第一共振峰处的幅值分别为11.05×10-8,6.12×10-8,4.19×10-8m·N-1。
(3)通过对钢弹簧阻尼参数对行车安全及车辆稳定性影响分析表明,增加钢弹簧阻尼,列车运行的安全性及舒适度均会提高,但在阻尼系数大于50 kN·s/m时对于行车安全及车辆稳定性的影响不明显,因此,设计时在保证隔振效果的前提下,综合考虑建议阻尼设置不宜超过50 kN·s/m。
