基于AprilTag的畜牧自主移动机器人建图与定位*

吕恩利，苏秋双，王飞仁，罗毅智 ，曾伯阳，曾志雄

(1. 华南农业大学工程学院，广州市，510642； 2. 广东机电职业技术学院，广州市，510550)

0 引言

定位是移动机器人算法中必不可少的组成部分。在室外场景中，研究者们大都使用全球卫星定位系统[1-2]为机器人提供定位，但畜牧机器人运行在没有卫星信号的室内，所以此类定位方法在畜牧机器人的应用上受到了限制。在定位方面，室内机器人大多使用激光雷达[3-5]、全景相机[6]和人工标志物[7-8]等方式。在这些方法中，采用人工标志物是一种低成本的方法，而在人工标志物中AprilTag又是一种较为灵活和具有鲁棒性的选择[9]。

Manfred Klopschitz[10]等基于sfm技术先确定相机位姿，然后在此基础上推算AprilTag位姿。Rafael Munoz-Salinas[11]等先通过AprilTag在各帧间的共视关系得到AprilTag之间的相对位姿，并以此为初值构建关于投影关系的最小二乘问题来优化AprilTag的位姿，最后再优化得到相机位姿。Pfrommer等使用因子图的方法在大场景中对AprilTag进行建图。不仅是在AprilTag位姿的测量上，在使用AprilTag为机器人提供定位上前人也有不少的研究，例如将AprilTag应用在水下机器人和无人机的定位上[12-13],但在这些研究中AprilTag位姿都是先验的，他们的研究都没有涉及AprilTag地图的建立。

前人在建立AprilTag地图和使用AprilTag定位上都做了不少的研究，但在移动畜牧机器人上为布置在环境中的AprilTag建立地图，并利用该地图为机器人提供定位的研究却不多。本文先使用机器人上的单目相机和轮式里程计估计出机器人的状态和布置在环境中的AprilTag的位姿；再以此为初值构建有关于投影关系最小二乘问题，进一步优化机器人和AprilTag的位姿；最后得到精度较高的AprilTag地图，并使用该地图为机器人提供定位。

1 机器人及算法相关介绍

1.1 算法原理

本算法的流程如图1所示，主要为两大部分，第一部分为状态估计部分，即图中的s1到s5，第二部分为位姿优化，即图中的s6到s9。

位姿优化由两部分组成，一个是在没有回环时利用局部地图优化抑制累计误差在地图中的增长，即图1中的s7；另一部分是检测到回环后利用全局优化消除累计误差以便能获得高精度的AprilTag地图，即图1中的s8。

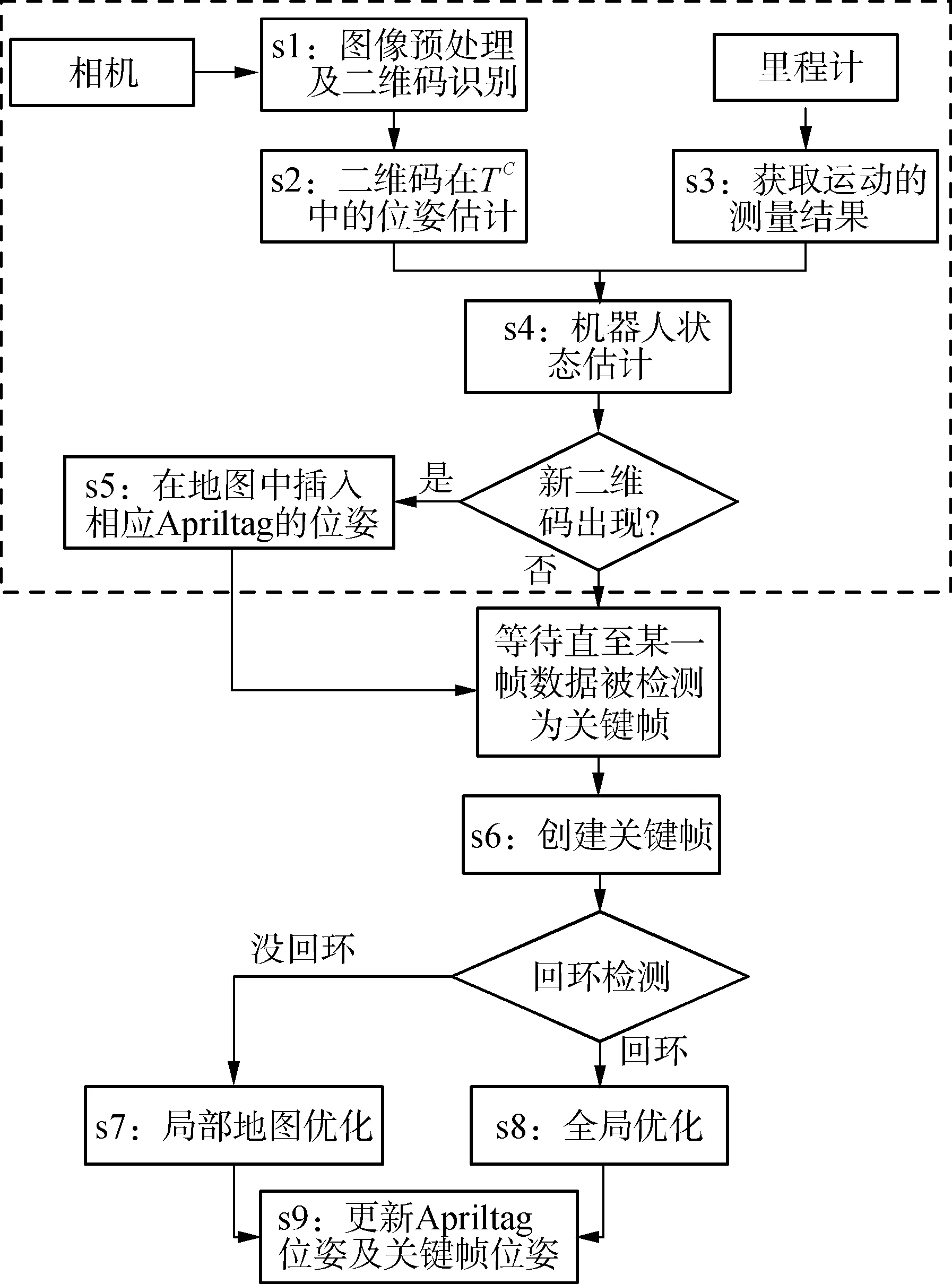
图1 算法流程图Fig. 1 Flow chart of algorithm

1.2 坐标系建立

机器人坐标系Tr：如图2所示，Tr以机器人的几何中心为原点，z轴垂直于地面竖直向上，x轴平行于地面指向机器人前进方向，y轴的正方向指向前进时的左侧，Tr始终与机器人固连在一起。

全局坐标系Tw：如图2所示，Tw与t=0时刻的Tr重合，但与Tr不同的是其不会随着机器人的运动而发生变化，而是始终固定不动。Tw是整个算法的基准，算法最终得到的机器人和Apriltag的位姿均是在这个坐标系下的位姿。

二维码(AprilTag)坐标系Tmi：如图2所示，Tmi(其中i代表该AprilTag的id号)的原点和AprilTag几何中心重合，x轴正方向指向右侧，y轴正方向向上，z轴正方向垂直于纸面指向外侧，且每一张AprilTag都有一个对应的二维码(AprilTag)坐标系。本文假设每张AprilTag的边长均为Ts(单位：m)。

机器人状态sr：由于机器人都在地板平面上运动，所以在全局坐标系中使用x，y(单位：m)和航向角θ(弧度制)便可以描述机器人的状态，即sr=[xyθ]T。

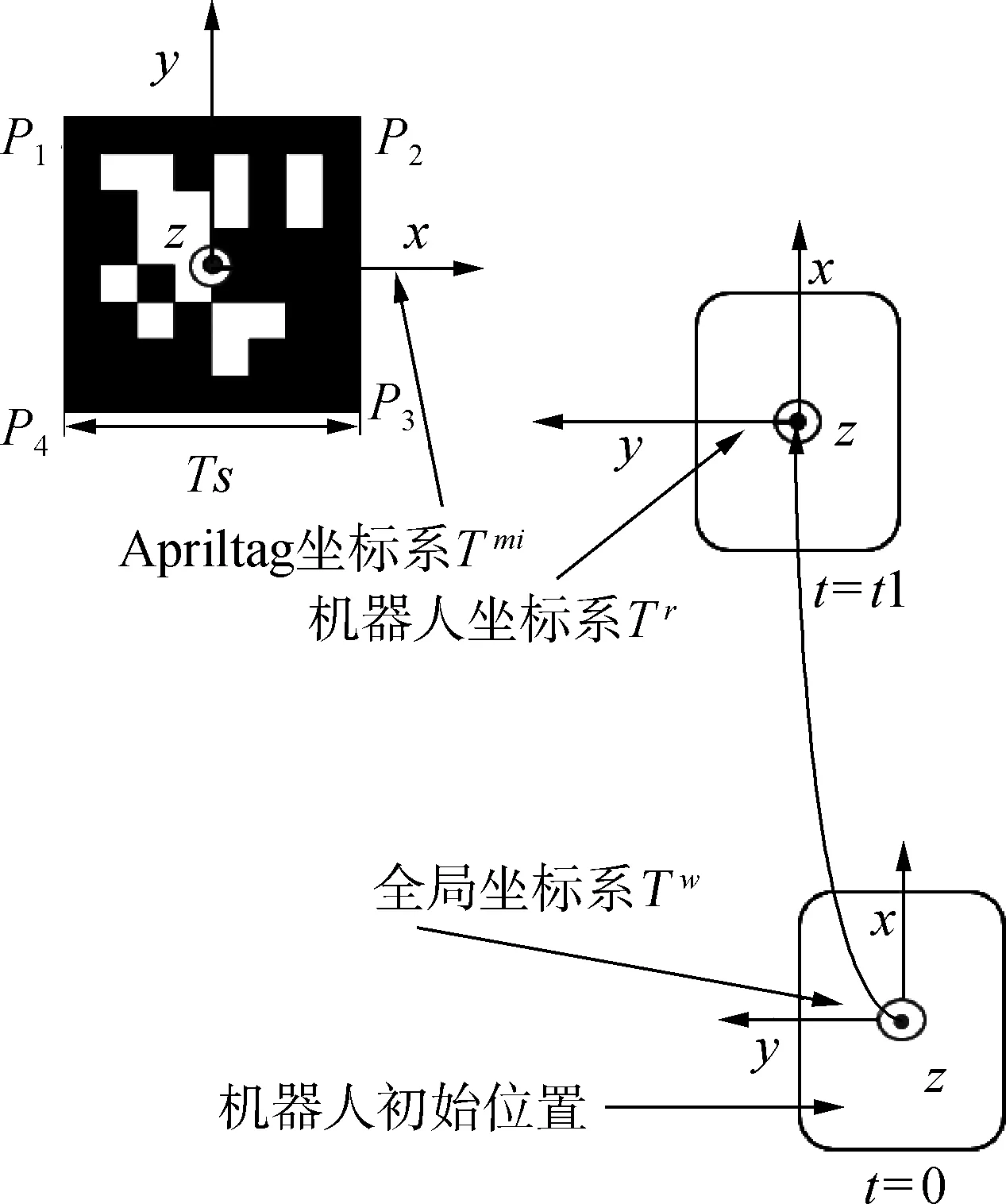
图2 各坐标系示意图Fig. 2 Diagram of each coordinate system

1.3 机器人结构

机器人大体结构如图3所示，机器人整体的长宽高分别为0.73 m，0.52 m，0.3 m，内部装载着一台工控机，用于电机的控制和传感器数据的接收处理等其他计算工作。Apriltag贴在机器人行走路线上方的天花板上，同时为了能够使得相机在天花板上拥有较大的成像范围，相机是以一定角度斜向上安装的，如图3(a)所示。

如图3(b)所示，机器人的驱动轮位于左右两侧，它们之间的间距为0.388 m，前后轮是支撑轮。工控机通过串口控制左右两侧电机，电机再驱动左右两驱动轮；两个电机均配备了编码器，可以实时的测量出左右电机转动量，结合轮子尺寸便可得到左右轮移动的距离。

(a) 移动机器人示意图

(b) 移动机器人底面示意图图3 机器人大体结构Fig. 3 General structure of robot

2 状态估计

2.1 AprilTag识别及其在相机坐标系中位姿估计

AprilTag的识别流程图如图4所示，在执行具体的识别操作之前要对图像做预处理，预处理包括将图像转换成灰度图、高斯滤波和图像的二值化。具体的识别过程可分为三个部分：直线提取、四边形检测和解码检测到的每个四边形[9]。直线提取是通过计算每个像素的梯度，然后采用根据梯度的大小及方向进行聚类的方法提取出图像中直线[9]；在获得图中所有直线的基础上，使用搜索树的方法[9]检测出它们所构成的所有四边形；最后通过对每一个检测出来的四边形做解码[9]来确定AprilTag的id，同时也能去除掉不是AprilTag的四边形，降低误检测率。

图4 Apriltag的识别过程

Apriltag的在相机坐标系中的位姿估计流程图如图5所示，利用Apriltag的四个角点在相机归一化平面上的投影坐标pij(i代表Apriltag的id号，j表示第几个角点)求解出Apriltag在相机坐标系中的两个局部极值，再以两个局部极值为初值分别迭代求解出两个更精确的值，最终比较两个解的误差，取误差较小者作为最终结果。

图5 AprilTag位姿估计的流程图

如图2所示，id为i的AprilTag的4个角点P1～P4在Tmi中的坐标分别为Pi1=[-0.5×Ts0.5×Ts0]T，Pi2=[0.5×Ts0.5×Ts0]T,Pi3=[0.5×Ts-0.5×Ts0]T,Pi4=[-0.5×Ts-0.5×Ts0]T。由于Apriltag的四个角点在一个平面上，所以存在单应矩阵H满足式(1)。

pij≅HPij(j=1,2,3,4)

(1)

式(1)中的pij表示某个角点在相机归一化平面上的坐标，由式(2)计算获得。

pij=CP-1pij′

(2)

式中：Cp——相机内参矩阵，本文认为内参矩阵是已知的；

pij′——点Pij在像素平面上的投影。

(3)

(4)

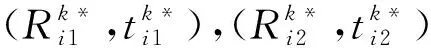
(5)

2.2 基于EKF的机器人状态估计

如图6所示，假设机器人经过一段时间的运动后状态由sr1转移到了状态sr2,在这一运动过程中，航向角的变化记为α(弧度制，本文的角度表示均为弧度制)，左右轮式里程计所记录的左右轮走过的距离分别为l,r(单位：m)。图6中的向量n1,n2分别是状态sr1，sr2时指向机器人前进方向的单位向量，m1,m2分别是垂直于n1,n2的单位向量，R为转向半径(单位：m)，机器人左右轮宽为d(单位：m)。不妨假设状态sr1和sr2如式(6)所示。

sr1T=[x1y1θ1],sr2T=[x2y2θ2]

(6)

图6 运动模型Fig. 6 Motion model

由几何关系得式(7),由图6可得式(8)。

R=ld/(r-l),α=(r-l)/d

(7)

(8)

将式(7)代入式(8)并整理得，当l≠r时状态转移方程如式(9)所示。当l=r时，状态转移方程如式(10)所示。式(9)和式(10)一起组成了状态转移方程，其中ε是均值为0高斯分布。

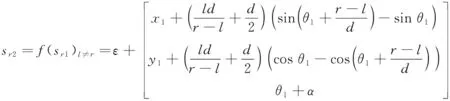
(9)

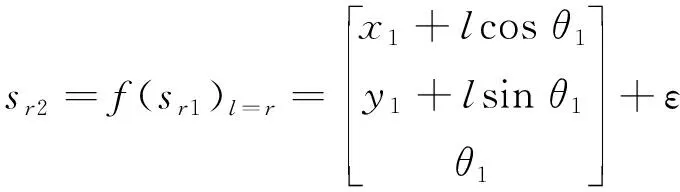
(10)

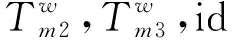
(11)

(12)

式中：Cke——相机内参矩阵的齐次形式。

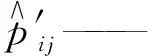
结合式(11)和式(12)，id号为2的AprilTag的观测数据可由式(13)给出。

(13)

其中δ是均值为0的高斯分布。

同理可求id号为3的AprilTag的理想观测g3，由此得机器人的观测方程为式(14)。

(14)

(15)

3 位姿优化

仅依靠上述方法估计AprilTag的位姿和机器人的状态，然后再依据式(15)增量式地扩展AprilTag地图的做法会使得累计误差在地图中快速增长，无法满足建图与定位精度的需求。为避免这一情况的出现，本文引入了位姿优化。

3.1 局部地图优化

局部地图优化只优化最新关键帧(当前关键Fc)所对应的机器人状态及最新关键帧所观测到的AprilTag的位姿。假设机器人在状态sr2时恰好满足关键帧生成条件，但并没有触发回环，其产生的关键帧记作F3，如图7所示。图7中标号1～4的正方形表示对应id号的AprilTag，Fk表示第k个关键帧，每个关键帧中带编号的四边形是该id号的AprilTag在该关键帧上的投影。

图7 观测示意图Fig. 7 Schematic diagram of observations

(16)

将式(16)代入式(12)中得式(17)。

(17)

由于每个旋转平移矩阵都可以表示为一个李代数，所以每一个集合Mpartial都对应着一个李代数的集合Mζ。图7的例子中，对应关键帧F3的李代数集合如式(18)所示。

Mζ3={ζ2,ζ3,ζ4}

(18)

局部优化的目的在于找到一组李代数Mbest使Mζ中对应的AprilTag的4个角点在所有属于集合F={Fpartial,Fc}的关键帧中的重投影误差最小，同时也为Fc找到一个状态srbest使得Mpartial中所有AprilTag在当前帧中的重投影误差最小。

第l个关键帧的重投影误差可表示为式(19)。

(19)

式中：a——第l帧中总共观测到了a张AprilTag；

srl——该帧对应的机器人状态；

pij——角点在像素平面上的投影。

结合式(19)，局部地图优化的目标函数可以由式(20)给出。

(20)

式(20)是一个最小二乘问题，这个问题的求解可以使用LM方法[17]，其初值由估计部分所提供。

3.2 全局优化

本算法在创建AprilTag地图过程中，会按照每张AprilTag出现的顺序为它们赋予一个序号。当某一关键帧中所观测到的AprilTag序号的差大于一定阈值时，便认为是回环了，此时便会启动全局优化。与局部地图优化类似，全局优化也是一个有关于重投影误差的最小二乘问题，也要确定两个集合Fglobal和Mglobal。

由于整个建图过程是以机器人起始状态为基准的，即以第一个关键帧为基准，所以第一个关键帧F1对应的机器人状态在全局优化中是被固定的。在全局优化中Fglobal和Mglobal分别为所有关键帧的集合和所有被观测到的AprilTag的集合，同时与局部地图优化类似Mglobal也对应着一个李代数的集合Mgζ。

类似的，全局优化的目的在于为每个关键帧(F1除外)找到一个对应的机器人状态sr(它们的集合记为sgbest)和一个李代数的集合Mgbest，使得所有的AprilTag的4个角点在所有关键帧中的重投影误差最小。结合计算某一关键帧中的重投影误差的式(19)，全局优化的目标函数如式(21)所示。

(21)

类似于式(20)，式(21)也可以使用LM方法求解[17]，其初值由局部地图优化提供。

4 试验与分析

机器人本体如图8所示，图中的nav350是用以提供机器人位置真值的传感器，其参数如表1所示。为验证本文所提算法，在一长约36 m，宽约10 m的区域内布置了126张AprilTag。布置时应保证任何时候相机均能观测到两张及以上的AprilTag，即控制AprilTag在环境中布置的密度。本文根据相机的成像范围，沿着机器人行走的方向大约每0.8 m布置一张AprilTag。

表1 nav350主要技术参数表Tab. 1 Main technical parameters of nav350

图8 机器人俯视图和侧视图

图9 试验环境及AprilTag提取的效果Fig. 9 Environmentof experiment and effect of AprilTag extraction

4.1 局部地图优化对累计误差的抑制

如图10(a)所示，在仅依靠估计部分估计机器人位姿的情况下，经过4 200帧后，算法给出的路径和真实的路径便有了明显的差距，此时路径的平均误差为0.324 3 m，最大误差2.043 m。引入了局部地图优化的算法得到的结果平均误差为0.042 2 m，最大误差0.339 8 m，和真实路径差距不大。可见局部地图优化在建图过程中对累计误差的有明显的抑制作用。

从图10(b)可以看出，随着帧数(时间的推移)的增加，仅靠估计部分得到的路径与真实路径的差距越来越大，平均误差增大到0.893 4 m，最大误差为5.06 m。虽然了引入了局部地图优化的算法得到的路径在经历了2 700帧后也开始与真实路径有了差距，平均误差为0.064 7 m，最大误差为0.339 8 m，但是其差距远小于前者。

(a) 4 200帧时的对比图

(b) 6 900帧时的对比图图10 定位效果对比Fig. 10 Comparison of positioning effect

4.2 AprilTag地图精度试验

由于直接测量AprilTag在全局坐标系中的位姿难度极高，所以直接将所建立的AprilTag地图与真值作对比是不现实的，本文将使用一种间接的方法来衡量所建立地图的精度。如果将所建立的AprilTag地图中的每个AprilTag作为路标点，在只运行机器人状态估计部分的情况下，机器人的定位精度便和AprilTag地图精度正相关，所以本文使用基于地图的定位(仅做状态估计)效果来衡量地图的精度。

建图时所有关键帧组成的路径和真实的路径对比图如图11所示，本算法给出的路径的平均误差为0.051 9 m，最大误差为0.223 3 m。

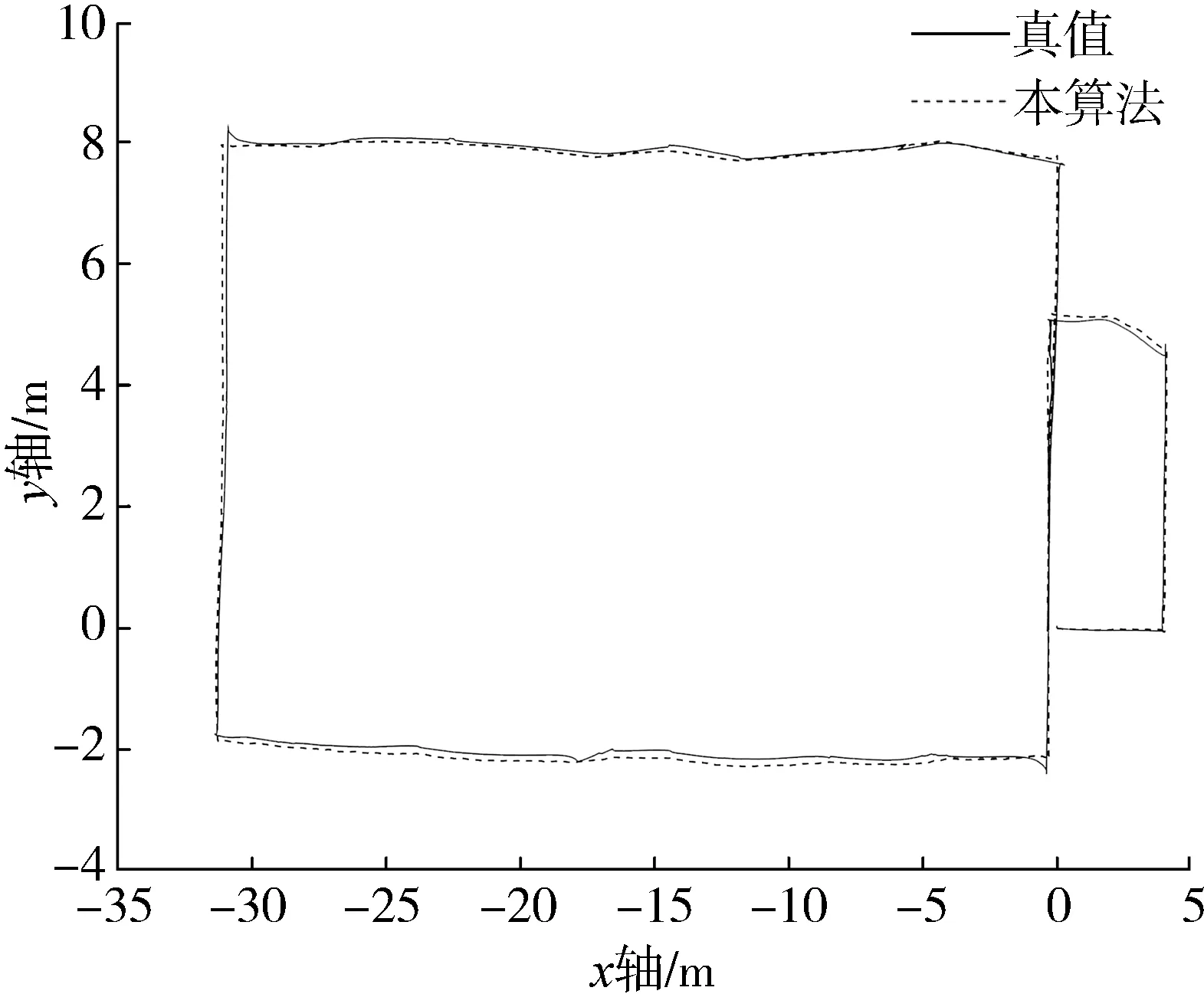
图11 关键帧对应的机器人状态与真值的对比图Fig. 11 Comparison diagram of robot state and truth value corresponding to key frame

在使用本算法给出的AprilTag地图的前提下，仅对机器人做状态估计得到的路径和真实值的对比图如图12所示，该定位效果的平均误差为0.075 86 m，最大误差为0.303 93 m，与建图时的误差相差不大。

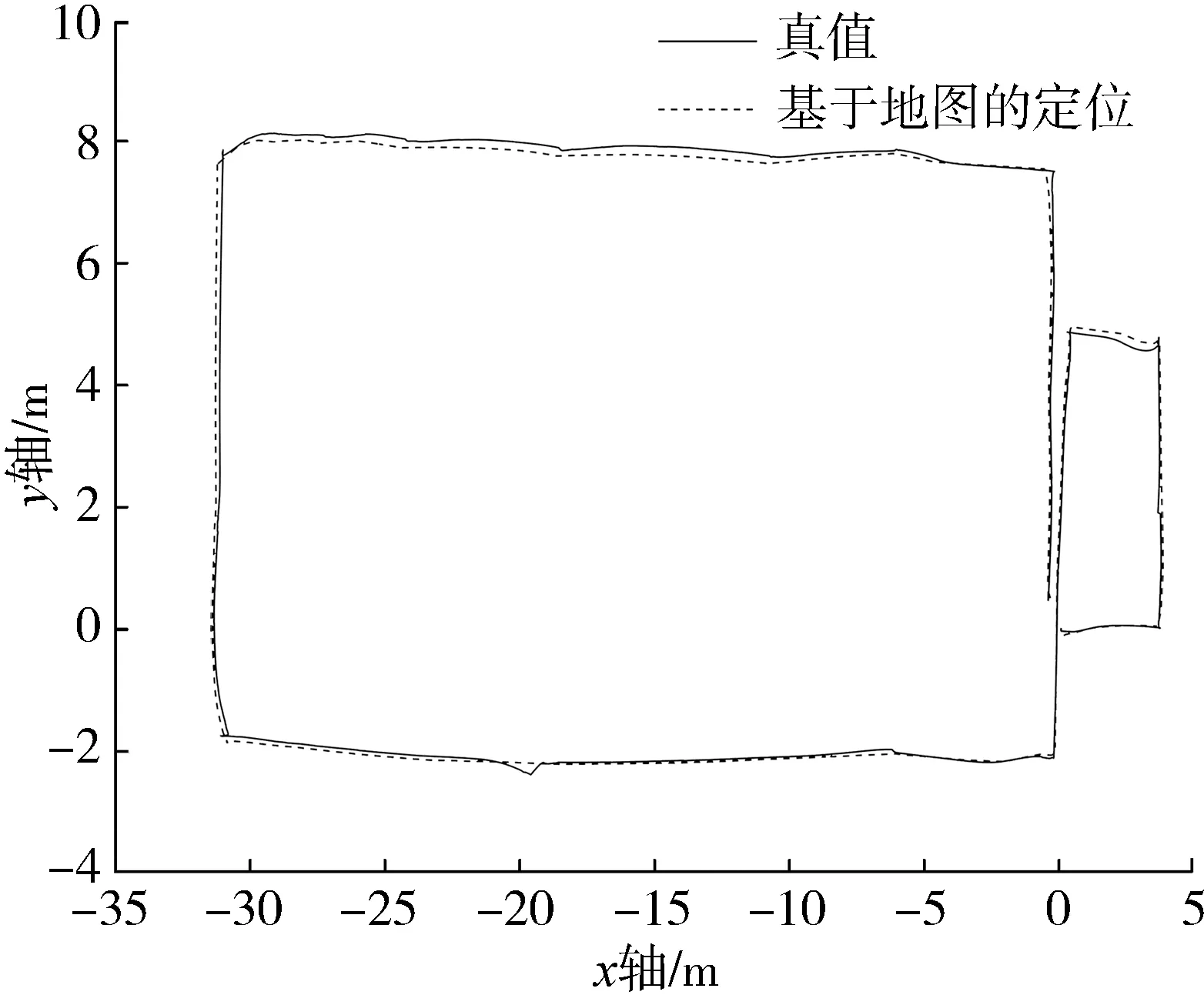
图12 基于本算法给出的地图的定位效果Fig. 12 Positioning effect of the map based on this algorithm

5 结论

1) 本文研究了在相机坐标系中估计AprilTag位姿的过程，先是利用AprilTag坐标系中角点的坐标和它们在相机归一化平面上的投影坐标计算出对应的单应矩阵；然后通过单应矩阵恢复出对应的旋转和平移。同时为了避免陷入局部极值，还估计出了第二组潜在解，最后以两组解为初值进行迭代求解，取误差较小的解作为结果。

2) EKF估计机器人的状态：根据机器人的运动模型给出了状态转移方程，同时也给出了机器人的观测方程，结合两个方程使用EKF估计机器人的状态。试验表明仅使用EKF估计机器人状态时会出现误差的累积。

3) 为了抑制和消除误差，本文引入了局部地图优化和全局优化。在没有回环时通过局部地图优化抑制误差的产生，检测到回环后使用全局优化来消除误差。文中分别给出了局部地图优化和全局优化时，目标函数的建立过程，同时采用LM方法来求解该问题。

4) 在建图过程中使用的局部地图的优化能显著的抑制累计误差的产生，且随着建图范围的增大，这种抑制效果越发明显。所以在大范围建立AprilTag地图时，特别是在有大回环的情况下，本文所提出的局部地图优化是必要的。

5) 在建图时各关键帧位置的平均误差为0.051 9 m，最大误差0.223 3 m；使用该地图为畜牧机器人定位时，其定位的平均误差为0.075 86 m，最大误差为0.303 93 m，能满足工作需求。基于地图的定位效果也间接验证了该建图算法能建立一张较为准确的AprilTag地图。