液力机械复合传动拖拉机动力系统匹配特性研究*

李贤哲，张辉，徐立友，刘孟楠，闫祥海, 3，张明柱

(1. 河南科技大学车辆与交通工程学院，河南洛阳，471003； 2. 拖拉机动力传动国家重点实验室，河南洛阳，471039；3. 中国一拖集团有限公司技术中心，河南洛阳，471039)

0 引言

液力机械复合传动(Series hydraulic and mechanical hybrid transmission，HMD)拖拉机以优异的阻力适应性和较低的换挡频率得以实用。HMD系统动力性能主要取决于柴油机与液力变矩器二者匹配情况，目前常用全功率匹配、部分功率匹配和折衷匹配等方式[1-3]。但是拖拉机作业工况复杂，载荷变化频繁，何种匹配方式都无法满足动力性与经济性的绝对平衡[4-5]。

国外，Kesy等[6]基于遗传优化算法将稳态特性建模误差作为质量依据，对预选液力变矩器匹配模型进行了估计。国内，王安麟等[7]提出液力变矩器负载特征泵轮转矩估计模型，解决了静态模型与其实际载荷特征的非关联性问题；常绿等[8]建立发动机与液力变矩器匹配优化模型，解决了匹配过程中功率分配不平衡的问题。然而，以往的仿真分析多以稳态为主，在发动机全油门状态下实现理想匹配，最优的匹配效果无法体现，而基于权重分配的匹配研究更符合拖拉机实际作业工况。

本文从拖拉机犁耕负载作业工况出发，建立发动机与液力变矩器匹配性能评价指标体系，基于熵权法—灰色关联分析理论搭建性能评估模型，确定HMD动力系统输出权重。以液力变矩器循环圆有效直径为优化目标，建立熵权—灰色关联度为目标函数，优化发动机与液力变矩器匹配特性区间，以期得到HMD系统科学合理的匹配方案。本文提出的动力优化匹配方案为液力机械复合传动拖拉机动力系统设计提供理论补充，同时为自主高端农机动力系统的发展提供新的技术路线参考。

1 匹配性能指标体系

图1为HMD拖拉机动力系统示意图。发动机按照车载仪器和动力输出装置的功率消耗扣除一定比率的外特性功率。根据发动机与液力变矩器的匹配原则，针对处于犁耕作业工况下的HMD拖拉机匹配性能评价指标体系补充，同时进行标准化和无量纲化处理。

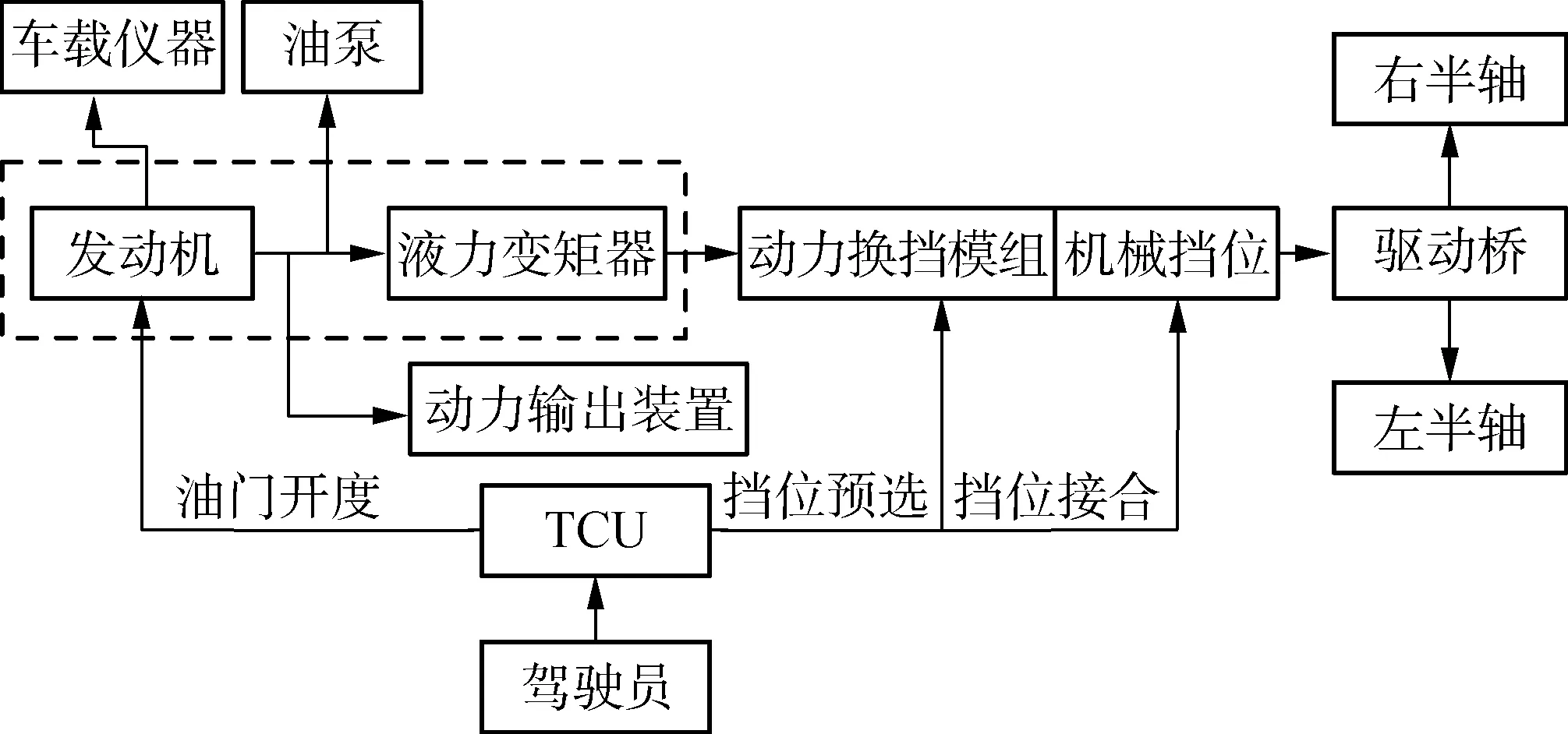
图1 HMD拖拉机动力系统示意图Fig. 1 Diagram of HMD tractor power system

1) 最大输出转矩系数δTM，表示拖拉机处于犁耕工况下克服较大负荷作业的能力，即

(1)

式中：Tgl——液力变矩器零速工况时负荷抛物线与发动机净转矩曲线交点处转矩，N·m；

Tmax——发动机最大净输出转矩，N·m。

2) 最大输出功率系数δNM，表示液力传动实际最高效率工况与理论工况的偏差度，即

(2)

式中：Pwmax——液力变矩器涡轮最大功率，kW；

PeH——发动机最大净输出功率，kW；

ηmax——液力传动最高效率。

3) 高效区工作宽度系数δw，表示发动机与液力变矩器处于高效区(η≥0.75)共同工作的转速范围，即

(3)

式中：n″w、n′w——液力变矩器特性曲线上效率为0.75时对应的涡轮转速，r/min；

nwmax——涡轮最大转速，r/min。

4) 功率输出系数δN，表示高效区工作范围内发动机功率的平均利用程度，即

(4)

5) 燃油消耗率系数δg，表示液力变矩器与发动机共同工作范围内燃油消耗比率，即

(5)

式中：gmax、gmin——发动机燃油消耗率最大值和最小值，kg/h；

综上所述，指标体系的建立为发动机与液力变矩器匹配性能定量分析提供了理论参考。由式(1)～式(5)，动力性评价指标

φD=aδTM+bδNM+cδw+dδN

(6)

经济型评价指标

φeco=eδg

(7)

式中：a、b、c、d、e——相应的权重系数。

2 熵权法评估模型

熵作为热力学物理概念引入信息论,反映体系混乱度与无序度，其数值大小表示系统混乱程度与携带相关信息量。信息熵基于热力学熵变原理，用于描述平均事件信息量丰富度,表示系统所包含的信息量的期望[9]。熵权分析法目前已经在工程技术、社会经济等领域得到了广泛的应用。熵权法利用信息熵根据各个指标离散程度计算权重，若评价指标熵值越大，则离散程度越小，其有效信息量相应越少，在综合评价中所占权重越小，反之亦然[10-11]。因此，利用信息熵理论计算各指标权重，为多指标综合评价提供依据。

设HMD动力系统匹配方案共有m种，以上述5种匹配性能指标体系为参考，可形成初始评价矩阵X={xij}5×m(1≤i≤5，1≤j≤m)，其中xij表示第i个样本中的第j项评价指标值，本文已对数据进行标准化处理，故可直接带入计算熵权，其对应的比重

(8)

则第j项评价指标的熵值

(9)

特别的，规定当Pij=0时，PijlnPij=0。

那么，各评价指标的熵权wj暨反映各指标间的离散程度，其值越大表明该指标对综合决策影响越大，有

(10)

3 灰色关联分析法评估模型

灰色关联法分析决策是结合问题实际情况确定出理想的最优序列，通过对比各个方案曲线几何形状的相似程度来判断其之间的关联程度[12]。灰色关联度针对系统发展变化态势的描述判定具有较高的精准度[13-14]。灰色关联分析法处理信息不完全明确的灰色系统具有一定的优势，对于小样本无规律指标的评价问题决策准确性较高[15-16]。

根据已确定的匹配性能指标体系，设p个数据序列形成以下矩阵

(11)

假定Y0为理想匹配方案，则Y0与Yp关于第s个元素的关联系数可以表示为

(12)

式中：σ——分辨系数，σ∈[0，1]。

其中Δmin=minp[mins(|y0(s)-yp(s)|)]，

Δmax=maxp[maxs(|y0(s)-yp(s)|)]。

由式(12)可以看出，分辨系数σ在一定程度上影响关联度的大小与方案排列顺序。因此，通过对分辨系数σ和熵权ws合理赋值，能够使得综合决策结果的准确性有较大提升。则第p个匹配方案的熵权—灰色关联度

(13)

综上所述，本文所提出的基于熵权法—灰色关联度分析理论的液力机械复合传动拖拉机动力系统优化匹配方案具体流程如图2所示。

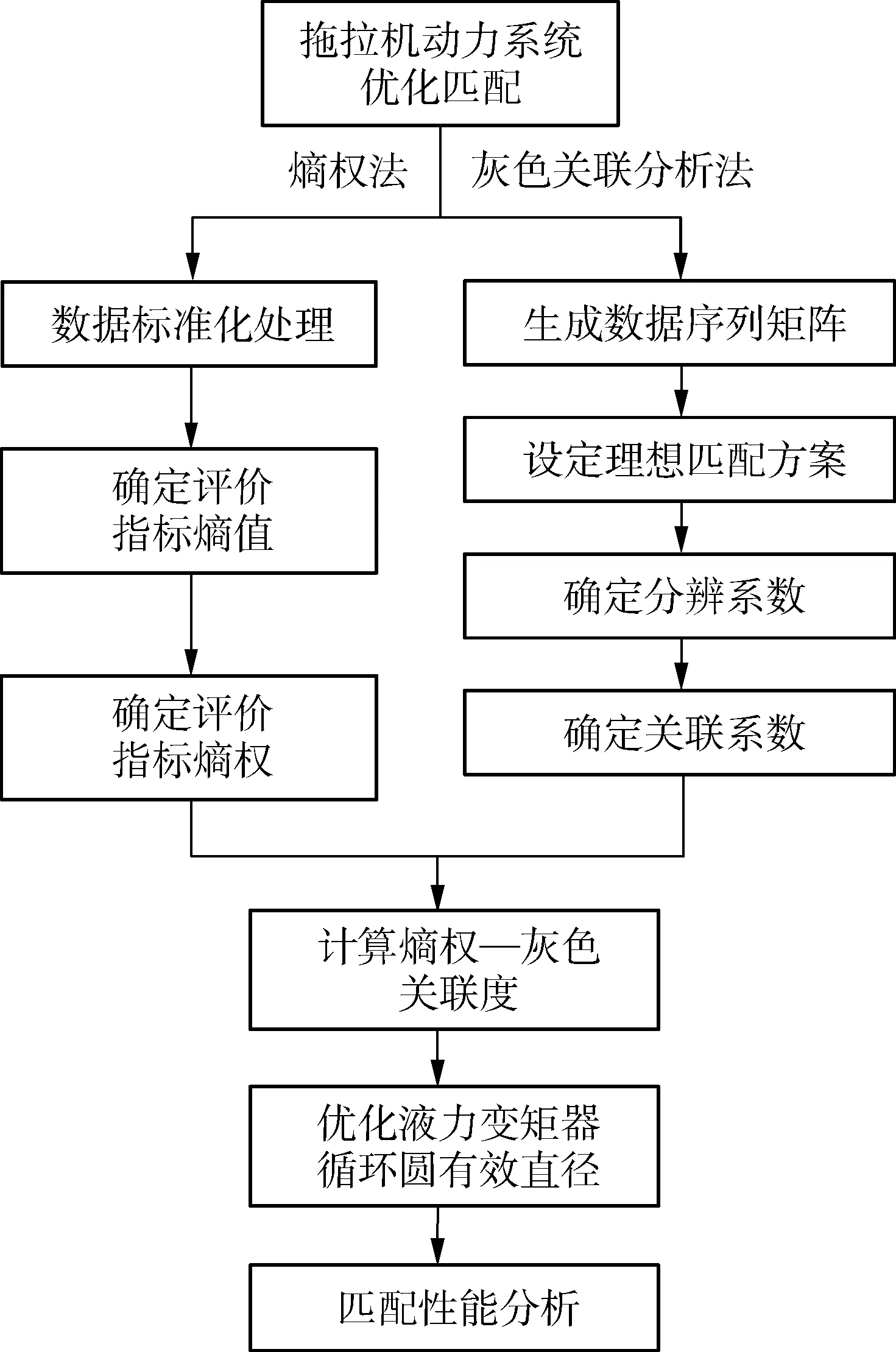
图2 HMD动力系统优化匹配流程图Fig. 2 Flow chart of HMD power system optimization and matching

4 实例分析

4.1 发动机模型

HMD1804拖拉机采用的发动机参数如表1所示。发动机的特性曲线由外特性段和调速段组成，其中外特性段由多项式拟合函数表示，而调速段从额定工况点到最大转速点近似为直线，由直线方程表示。

表1 HMD1804发动机基本参数Tab. 1 Basic parameters of HMD1804 engine

设发动机转矩曲线方程为

(14)

式中：a0，a1，a2，…，an——多项式拟合函数待定系数；

b0，b1——一次项拟合函数待定系数；

ne——发动机转速离散值，r/min；

Te——发动机转矩离散值，N·m。

采用三次多项式进行拟合，并使用Matlab编程求解，结果如表2所示，可以看出，相对误差最大控制在8%以内，主要原因是转速处于1 100 r/min时，发动机接近怠速工况，输出功率处于提升状态，转矩波动较大。

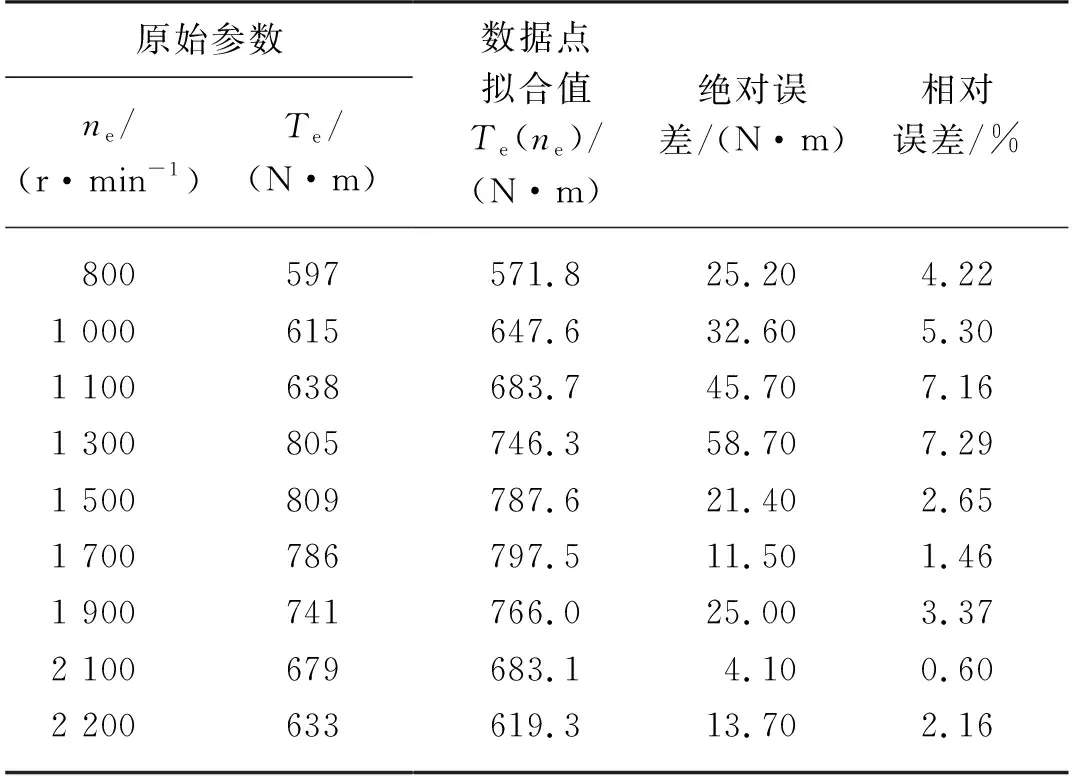
表2 三次多项式拟合结果Tab. 2 Results of cubic polynomial fitting

根据拟合结果，绘制发动机外特性曲线如图3所示。可以看出，发动机输出转矩在外特性段随转速变化较为缓慢，在1 700 r/min时达到峰值797.5 N·m；转速区间在[1 800，2 200]时，输出功率能够达到最大值132.1 kW，此阶段功率变化相对平缓，可以看作恒功率输出。比油耗特性曲线在发动机整个工作范围内变化缓慢，当转速达到1 500 r/min时，燃油消耗率处于谷底为212.4 g/(kW·h)。

(a) 发动机扭矩、发动机功率

(b) 燃油消耗率图3 HMD1804发动机外特性曲线Fig. 3 External characteristic curve of HMD1804 engine

4.2 液力变矩器优化模型

液力变矩器的选择以相似性原理设计方法为依据[17-18]，其原始特性参数是已经给定的，如表3所示，而变矩器有效直径才是影响其与发动机匹配的关键性因素。因此，将变矩器循环圆有效直径Di作为设计变量，令X=[x]T=[Di]T，并将熵权—灰色关联度函数作为优化目标函数。

表3 液力变矩器基本参数Tab. 3 Basic parameters of hydraulic torque converter

灰色关联系数矩阵如表4所示。

根据发动机外特性和液力变矩器原始特性曲线，基于匹配性能评价指标体系，采用熵权法式(9)、式(10)，计算不同变矩器循环圆有效直径下各指标熵权wi，利用灰色关联分析法式(12)，取分辨系数σ=0.64，计算得到灰色关联系数矩阵。

表4 灰色关联系数矩阵Tab. 4 Grey correlation coefficient matrix

那么，各匹配性能评价指标的综合权重

[a,b,c,d,e]=[0.176，0.185，0.227，0.218，

0.194]

由式(13)计算得到熵权灰色关联度

τ0=[0.649,0.651,0.724,0.715,0.601]

循环圆有效直径Di对应目标函数值，绘制相应关系，如图4所示。从图4可以看出，当循环圆有效直径为374.588 mm时，目标函数达到最大，其值为0.773，此时液力变矩器与发动机的匹配性能即为最优。

图4 变量与目标函数关系Fig. 4 Relationship between variable and objective function

根据优化后得到的理想循环圆有效直径D0，绘制液力变矩器基本牵引特性曲线，如图5所示。可以看出，能容系数基本覆盖整个液力变矩器工作区间，泵轮轴吸收功率能力符合拖拉机驱动要求，液力变矩器高效区转速比范围为[0.39，0.85]，最高效率为89.4%，此时对应转速比为0.65，能容系数为5.5×10-3。

(a) 变矩系数、变矩器效率

(b) 能容系数图5 液力变矩器牵引特性曲线Fig. 5 Traction characteristic curve of hydraulic torque converter

4.3 匹配性能分析

由前述分析可知拖拉机发动机与液力变矩器匹配时，全功率匹配和部分功率匹配分别是两种极限形式[19-20]。重载作业工况时以全功率匹配，发动机将更多功率输出到传动系统；轻载作业工况时以部分功率匹配，拖拉机则作业动作迅速，提高作业效率。因此，基于熵权—灰色关联度分析计算结果，对优化后的液力变矩器与发动机进行匹配特性分析，如图6～图9所示。

图6为全功率、部分功率和优化匹配共同工作输入特性曲线。从图6可以看出，优化后的液力变矩器高效区输入特性曲线通过发动机恒功率区间，且与部分功率匹配特性区间重合，共同工作点泵轮转速范围为[2 261，2 373]。

图6 共同工作输入特性对比Fig. 6 Comparison of co-working input characteristics

图7为全功率、部分功率和优化匹配共同工作输出特性曲线。从图7可以看出，优化匹配后的发动机工作转速有所降低，减少了振动和噪声，提高了使用寿命。涡轮最大输出扭矩可以达到1 611.3 kN，但在实际使用时，涡轮转速分布规律f(nw)随拖拉机外载荷呈现不规则变化，因此采用均匀分布计算方法获得接近实际的特性，有

(15)

图7 共同工作输出特性对比Fig. 7 Comparison of co-working output characteristics

则高效区平均输出功率为

(16)

图8为效率特性对比曲线。从图8可以看出，优化后的液力变矩器取得了较好的匹配效果，高效区涡轮转速范围为[814，1 562]，在涡轮转速处于1 365 r/min时，可以达到最高液力传动效率为89.3%，相较于其他匹配方式平均效率提升约2.3%，动力性优化符合评价指标要求。

图8 效率特性对比Fig. 8 Comparison of efficiency characteristics

图9为燃油消耗率对比曲线。从图9可以看出，液力变矩器涡轮工作处于高效率区间时，优化匹配后的燃油消耗率相对于全功率匹配减少7.3%，相对于部分功率匹配减少3.1%；当涡轮转速达到1 283 r/min时燃油消耗率处于谷底，此时的燃油消耗率为246.5 g/(kW·h)，HMD拖拉机经济性得到较大提升。

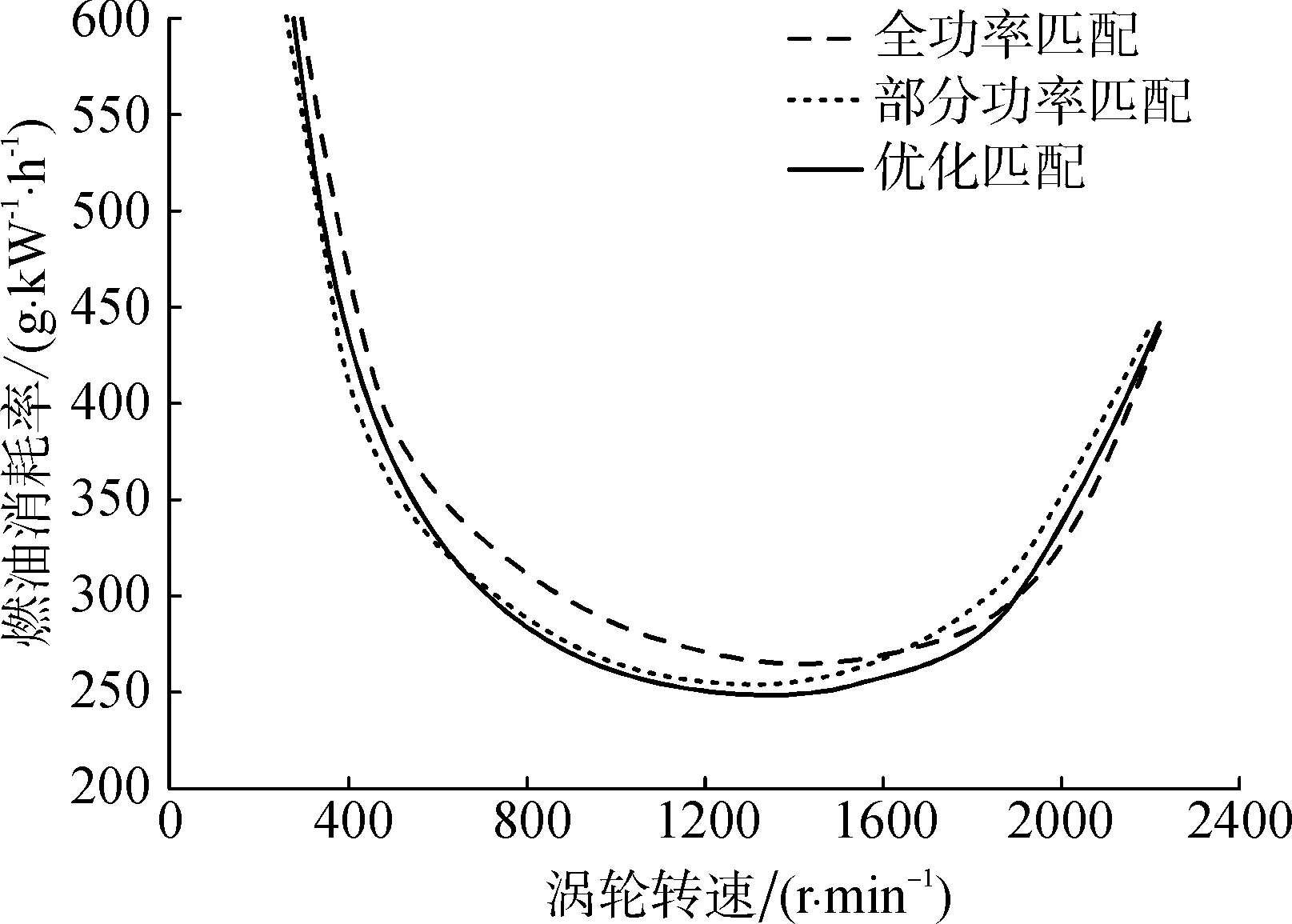
图9 燃油消耗率对比Fig. 9 Comparison of fuel consumption ratio

5 结论

1) 根据HMD拖拉机实际犁耕作业工况，针对动力系统提出新的评价指标体系，确定权重表达关系式，建立熵权法和灰色关联度分析法评估模型，通过实例分析，得到发动机与液力变矩器相对合理的匹配方案。

2) 基于Matlab三次多项式拟合函数，对发动机外特性模型优化，结果表明：优化后的发动机输出特性误差在8%以内，峰值扭矩为797.5 N·m，恒功率输出区间内输出功率最大值达到132.1 kW。

3) 基于熵权—灰色关联度分析方法对液力变矩器模型进行优化，确定循环圆有效直径为374.588 mm，高效区涡轮转速范围为[814，1 562]，平均输出功率为91.2 kW。匹配结果表明：优化后的动力系统平均传动效率提升约2.3%；燃油消耗率相对于全功率匹配减少7.3%，相对于部分功率匹配减少3.1%，能够较大程度兼顾HMD拖拉机作业时的动力性与经济性。