高产气井油管柱双重非线性流致振动模型研究
2022-04-23王国荣方达科魏安超柳军
李 中,王国荣 ,方达科,魏安超,柳军
1.中海石油(中国)有限公司湛江分公司,广东 湛江 524057;2.西南石油大学机电工程学院,四川 成都610500
引言
中国高温高压天然气资源丰富,在高产气井生产过程中,油管柱(图1)受高速流体的影响,极易发生纵横向耦合非线性振动和油套管非线性接触碰撞。这将导致管柱局部产生交变荷载和动态应力,管柱发生疲劳损坏;管柱上端受到较大的拉应力,管柱发生强度破坏;同时将增大管柱轴向压力,使其发生屈曲变形,增加油管与套管之间的摩擦磨损量,发生摩擦穿孔破坏[1](图2)。因此,亟需开展高产气井油管柱非线性振动模型研究,为中国高产气井的安全开发奠定理论基础。
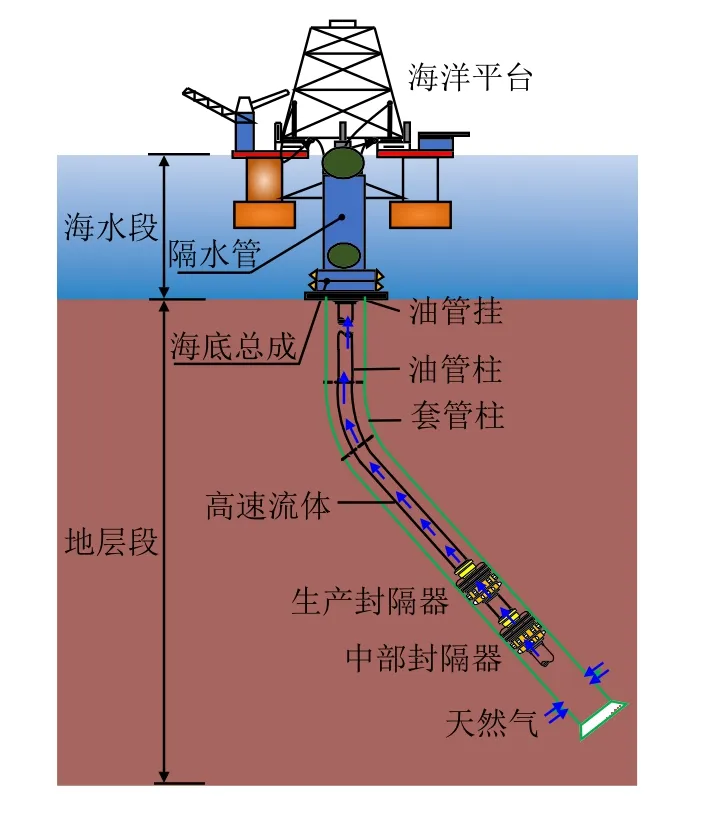
图1 高产气井管柱结构图Fig.1 Tubing string structure of high-yield gas well

图2 管柱振动引起的失效问题Fig.2 Failure problems caused by vibration of tubing string
国内外学者针对考虑内流引起的管柱振动问题,开展了大量研究,并取得了一些成果。早期学者针对内流作用下的管柱振动问题开展了初步研究[2],通过实验验证了内流对管柱的动力响应有显著影响[3]。随后,诸多学者针对管柱振动模型开展了详细研究,建立了流体作用力的计算方法[4]、管柱纵向振动[5]、横向振动[6]以及流固耦合振动模型[7],在此基础上,分析了管柱的振动响应特性。近年来,部分学者[8-10]发现细长管柱的纵横向耦合效应明显,不可忽略,邢誉峰等[11]针对梁的纵横向振动问题,建立了梁的纵横向耦合振动方程,阳明君等[12]针对尤拉屯气田完井管柱的振动问题,采用有限元方法ANSYS 建立高产气井大长径比管柱振动模型,Liu 等[13]考虑管柱的几何非线性问题,建立了海洋立管的纵横向耦合振动模型。可见,对于细长结构的振动分析,不能忽略其几何非线性因素(即纵横向耦合振动),高产气井油管柱属于典型的细长结构(长径比约30 000)。
高产油气井油管柱一旦发生纵横向耦合振动,极易使其产生非线性接触碰撞。目前,针对油套管非线性接触碰撞问题,研究主要集中在钻柱或管柱发生屈曲后的接触问题[14-16],得到管柱屈曲后接触力的静态计算方法,这与生产工况下管柱流致振动引起的动态接触碰撞具有一定的差别。国内外学者针对流致振动引起的接触碰撞问题,主要建立了换热管束与支承板接触碰撞力的计算方法,Rogers 等[17]和Ting 等[18]采用动态有限元法预测了单个换热器与支承板之间的接触碰撞力,将预测结果与实验数据进行了对比,验证了预测方法的正确性,但未给出具体的计算方法。丁传义等[19]和沈时芳等[20]开展了换热器传热管与支承板之间接触碰撞力的计算方法研究,得到单一位置接触的碰撞力计算方法和碰撞力的时程响应,并与实验数据对比,验证了计算方法的正确性,但模型只考虑一点位置的接触碰撞,对于多位置的接触碰撞未开展相应的研究。
因此,本文针对高产气井高速流体诱发油管柱振动引起的破坏问题,开展油管柱非线性流致振动模型研究和振动模拟实验研究,为中国高产气井油管柱的安全设计提供理论分析。
1 高产气井油管柱双重非线性流致振动模型建立及求解
1.1 油管柱纵横向耦合非线性流致振动模型
管内的高速流体是引起油管柱振动的主要因素,由于油管柱属于细长结构,易产生纵向和横向振动,纵向和横向振动又不是单独分开运动,它们之间相互影响,因此,需建立油管柱的纵横向耦合动力学模型。
本文建立以深度方向为x轴,水平向右为y 轴的平面坐标系(图3)。
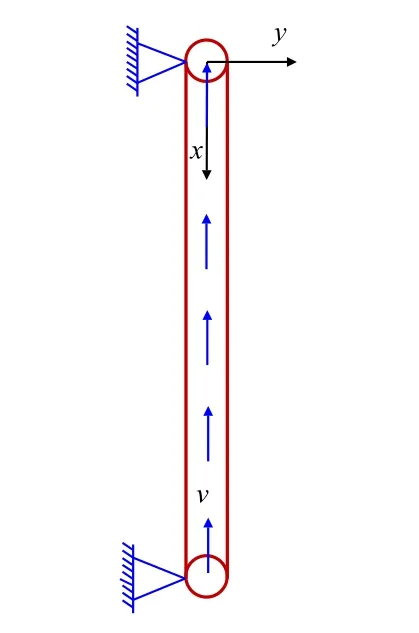
图3 油管柱物理模型Fig.3 Physical model of tubing string
把油管简化为均匀的Rayleigh梁,若考虑纵横耦合,其几何关系为[11]
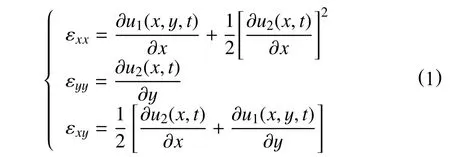
式中:εij—6 个应变分量,i,j=x,y;
y—厚度坐标,m;
u1(x,y,t),u2(x,t)—与坐标系(x,y)对应的位移场函数,m。
其表达式为
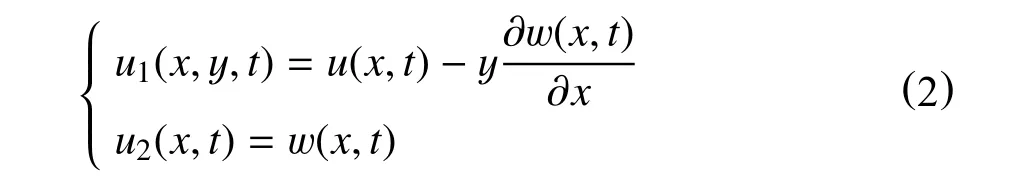
式中:u(x,t)—纵向位移,m;
w(x,t)—横向位移,m;
t—时间,s。
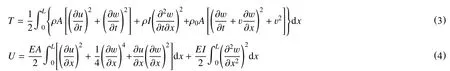
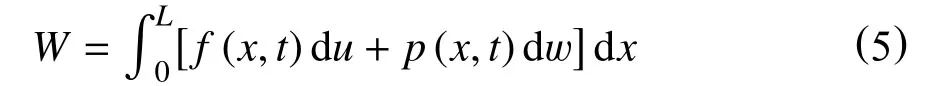
式中:
T—油管的动能,J;
U—油管的应变能,J;
W—外力做功,J;
L—管长,m;
ρ,ρ0—油管密度和流体密度,kg/m3;
A—油管横截面积,m2;
I—油管截面的惯性矩,m4;
E—油管弹性模量,Pa;
f(x,t),p(x,t)—油管受到的纵向和横向外激力函数,N。
根据哈密顿(Hamilton)变分原理,建立油管的振动微分方程

式中:
δ—油套管接触后产生的形变,m。
由式(3)∼式(6)化简得油管的纵向、横向振动微分方程
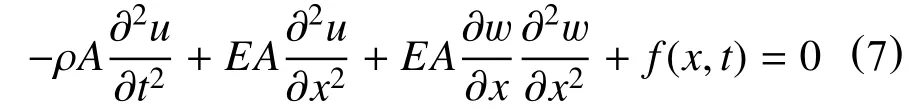
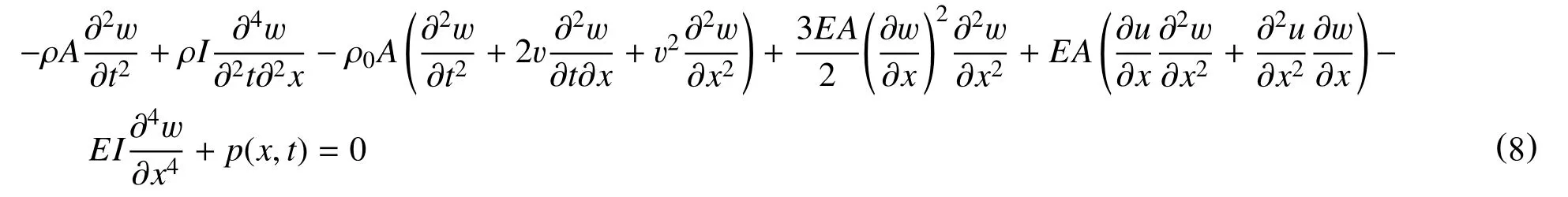
由于上端为油管挂,下端为封隔器,把上下端视为固定端,即边界条件和初始条件为
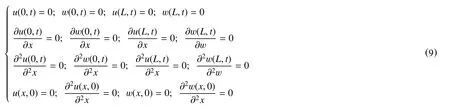
1.2 油管与套管非线性接触碰撞模型
在内部高速流体的作用下,油管柱会产生横向和纵向振动,当横向振动位移达到套管与油管之间的间隙时,油管与套管发生接触碰撞,纵向产生接触摩擦,造成油管表面摩擦磨损。因此,在纵横向耦合振动下,考虑油管与套管的接触碰撞效应是进行油管疲劳磨损分析的必要条件。
1.2.1 套管与油管碰撞力-变形非线性关系
根据弹塑性力学理论,建立油管碰撞力与形变之间的关系。变形结构如图4 所示,油管发生碰撞,油管上的A2点变形到了套管上的A1点。

图4 油管与套管接触变形示意图Fig.4 Schematic diagram of contact deformation betweentubing-casing
由几何关系得
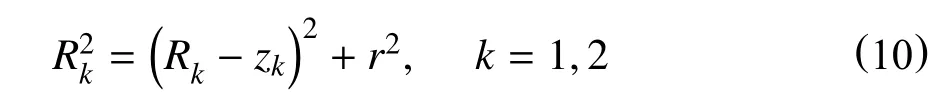
式中:
R1,R2—套管、油管的半径,m;
z1—套管接触点到套管内壁的径向距离,m;
z2—油管接触点到套管内壁的径向距离,m;
r—接触点到油管轴心的水平距离,m。
在力的作用下,套管和油管发生变形,它们之间的形变为δ,并产生了宽为2b的接触带。由几何关系可得
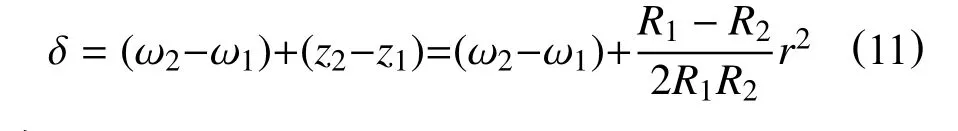
式中:
ω1—套管接触后轴向产生的位移,m;
ω2—油管接触后轴向产生的位移,m。
若接触带的宽度比油管的半径小得多,则每个管柱都可以近似地当作弹性半平面来考虑,由文献[21]可得ω1和ω2的计算公式

式中:µ1,µ2—套管和油管材料泊松比,无因次;
E1,E2—套管和油管材料弹性模量,Pa;
2b—油套管接触带宽度,m;
q(x)—套管和油管均布载荷,N;
p—油套管接触力,N。
将所得的ω1,ω2代入变形条件
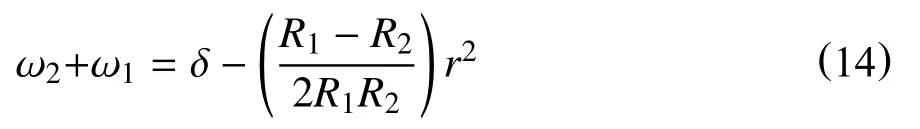
假定q(x)是与以2b为直径所作的半圆弧纵坐标成比例,得

将E1=E2=E、µ1=µ2=0.3 代入式(12)和式(13)中,得油管碰撞力与变形的关系式

1.2.2 套管与油管动态碰撞力与摩擦力的计算
套管与油管接触碰撞问题可以简化为多节点发生接触碰撞问题,因此,研究套管和油管某一个点接触,得到套管对油管碰撞力的计算方法,然后把计算方法应用到管柱的每个节点。
套管与油管发生碰撞后如图5 所示。
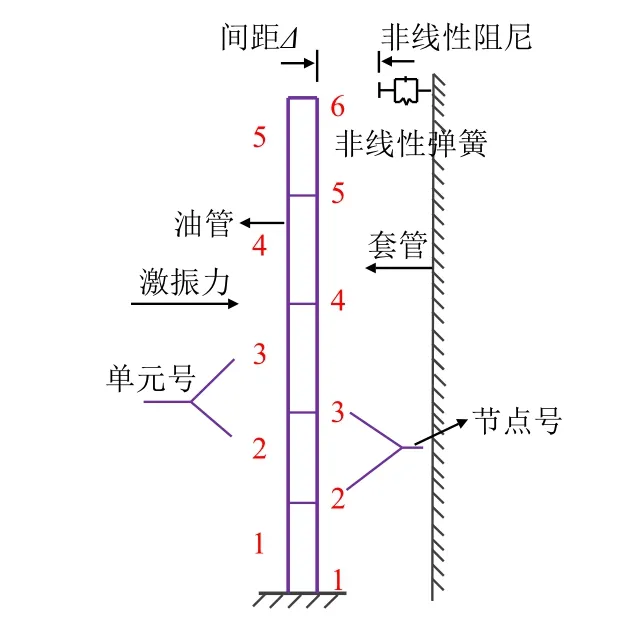
图5 油管与套管碰撞示意图Fig.5 Schematic diagram of tubing-casing collision
假设碰撞时油管受到“弹簧-阻尼器”的作用,因此,油管与套管发生碰撞,套管将给它施加一个碰撞力和碰撞阻尼力,碰撞力根据式(16)得到,阻尼力计算公式为[20]

式中:
pc—接触阻尼力,N;
c—碰撞阻尼系数,无因次,c=1.5ap;
a—常数,无因次,对于钢材,a=0.2∼0.3[22];
碰撞阻尼力也是变形的非线性函数。由此可得气井油管与套管非线性碰撞力和摩檫力计算公式

式中:
F—油套管接触碰撞力,N;
f—油套管摩檫力,N;
µ—油套管摩擦系数,一般取0.3[23]。

1.3 双重非线性模型的求解
1.3.1 双重非线性模型离散
本文采用线性拉格朗日函数和三次埃尔米特函数表达管柱的纵向位移u和横向位移w,根据文献[13]可知有限元离散形式为

式中:
l—单元的长度,m;
d—管柱单元位移矩阵;
ψ—管柱单元纵向位移形函数矩阵;
φ—管柱单元横向位移形函数矩阵。
把位移函数式(20)和式(21)代入能量泛函,可以得到用结点位移向量表示的应变能函数U、动能函数T的标准形式,即
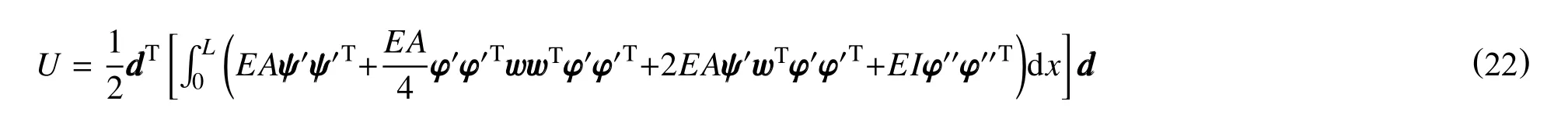

式中:
w—油管横向位移矩阵。
把结构单元组装后,根据变分原理可得系统的离散形式动力学方程

式中:
D,M,C,K,F—系统的位移矩阵、质量矩阵、阻尼矩阵、刚度矩阵和载荷列向量,具体元素见式(20)和式(21)。
1.3.2 Newmark-β 求解方程
本文采用Newmark-β 逐步积分的求解方法,避免了任何叠加的应用,能很好地适应非线性模型。
Newmark-β 法假定

式中:
β,γ—按积分的精度和稳定性要求进行调整的参数。本文取β=0.5,γ=0.25,即假定从t到t+∆t时刻的速度不变,由式(25)和式(26)可得

考虑t+∆t时刻的振动微分方程为
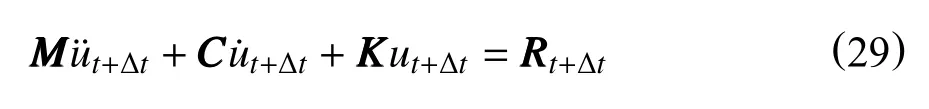
因此,可得模型的求解流程如图6 所示,并采用Fortran 语言编写了相应的数值计算程序。
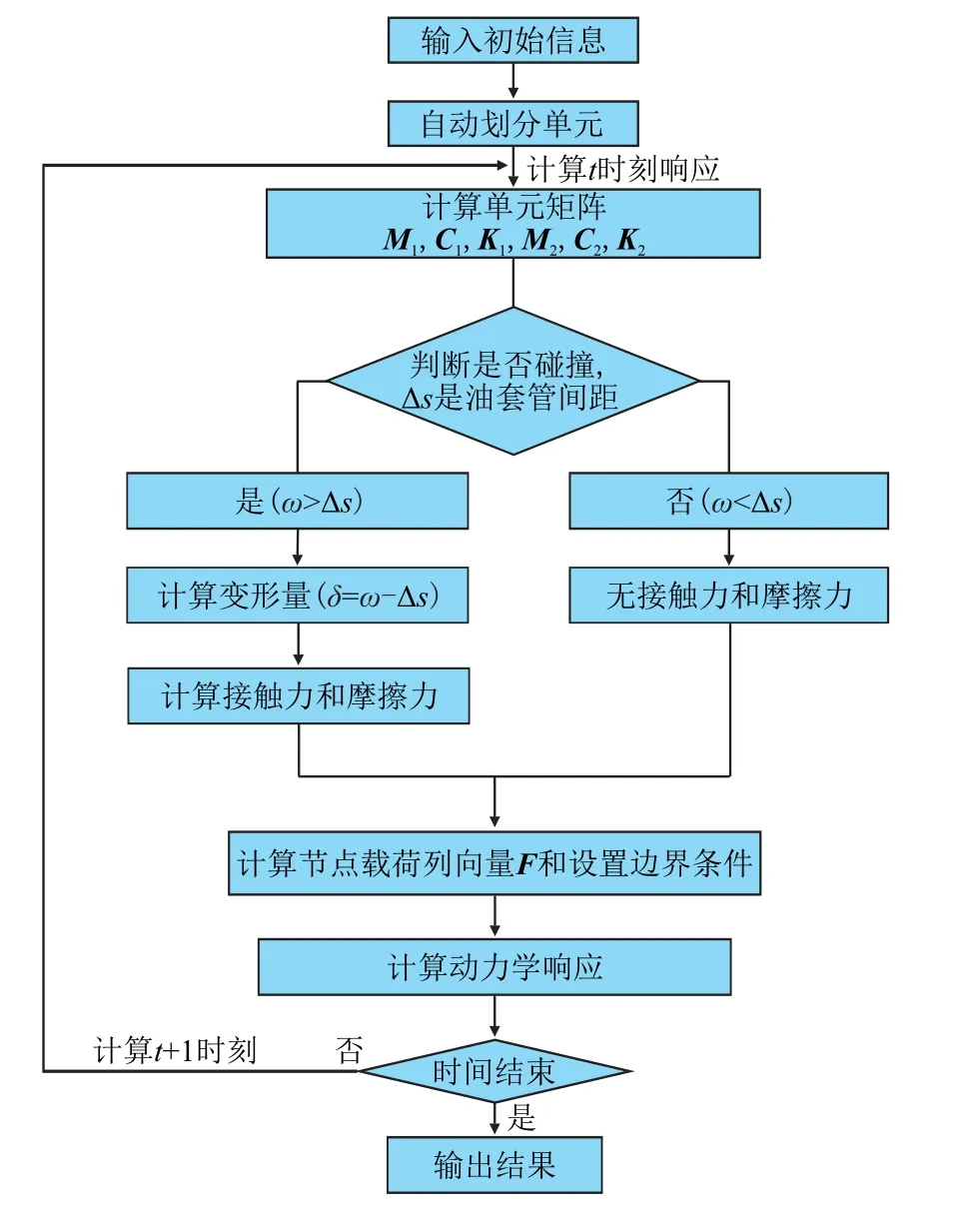
图6 计算流程图Fig.6 Computing flow chart
2 高产气井油管柱双重非线性流致振动模型验证
2.1 油套管非线性接触碰撞模型验证
本文采用文献[20]相同参数(表1),具体结构如图7 所示,通过设置4 处外激励载荷,中间位置两边设置弹簧阻尼,采用本文建立的双重非线性模型,计算管柱的碰撞力,并与文献的实验结果和文献模型计算结果对比,验证本文双重非线性碰撞模型的正确性和有效性,文献模型与本文模型的区别主要体现在文献只考虑单一接触碰撞非线性影响,而本文模型考虑了纵横向耦合和接触碰撞双重非线性的影响。

图7 管柱接触碰撞结构图Fig.7 Contact collision structure diagram of pipe string

表1 计算模型参数Tab.1 Calculating model parameters
图8 给出了单非线性模型、双重非线性模型和实验结果的接触力时程响应曲线。从图中可以看出,本文提出的双重非线性模型计算结果在振幅和变化规律上都比文献[20]中的单非线性模型计算结果更接近实验结果。双重非线性模型比单非线性模型更能反映系统的高频响应特性,验证了本文双重非线性模型的正确性和高效性。
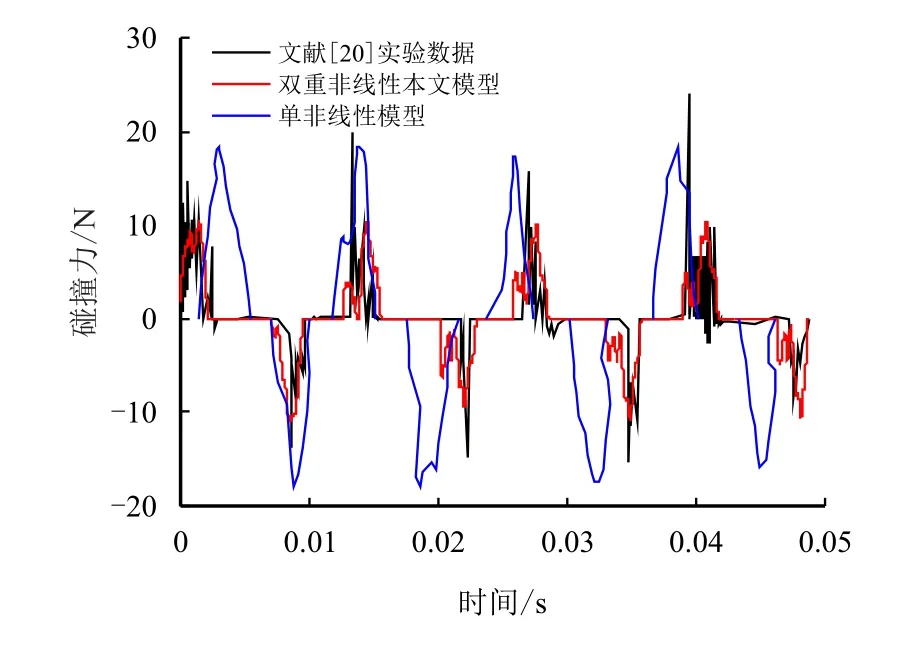
图8 接触碰撞力计算结果图Fig.8 Calculation results of contact/collision force
2.2 油管柱双重非线性流致振动模型实验验证
2.2.1 模拟实验参数设计
由于现场无法测得有效的振动数据验证本文模型的正确性,故借助模拟实验方法验证模型的正确性。管柱振动模拟实验应满足3 个标准:几何相似性、运动相似性和动力相似性[24-25]。本文采用几何相似法设计了模拟实验中油管和套管的基本尺寸(内径、外径、管长等),由于长度方向与径向尺寸差异较大,故不采用相同比例,径向和纵向的相似比分别设置为5.0 和438.0。根据黄涛[26]和李子丰等[27]的研究,实验管柱的材料密度和弹性模量与其对应的实际管柱应满足

式中:ρp—实际管柱的密度,kg/m3;
ρm—模拟实验管柱的密度,kg/m3;
Ep—实际管柱的弹性模量,Pa;
Em—模拟实验管柱的弹性模量,Pa;
λ—相似比。
将实际管柱的密度ρp=7 850 kg/m3和弹性模量Ep=210 GPa 代入式(30),得

根据弹性模量和密度的比值,通过查材料手册,选择PE 管比较符合要求,其弹性模量和密度分别是Em=6.0 GPa 和ρm=1 200 kg/m3。
根据现场气田的实际情况[地层压力46.7 MPa,产量(100∼200)×104m3/d,地层温度150°C,地温25°C,标准大气压0.1 MPa],通过状态方程计算,可以确定管内类似流体速度。

式中:p1—现场工况的压力,Pa;
V1—现场工况的体积,m3;
T1—现场工况的温度,K;
p2—模拟实验工况的压力,Pa;
V2—模拟实验工况的体积,m3;
T2—模拟实验工况的温度,K;
v′—模拟实验的流速,m/s;
s—模拟管内横截面积,m2。
通过以上分析计算,得到本模拟实验参数,如表2所示。

表2 模拟实验参数Tab.2 Simulated test parameters
2.2.2 模拟实验系统设计
本文实验系统主要由注气子系统、管柱子系统和连接子系统组成(图9),具体包括气源(螺杆空气压缩机、储气罐)、管道、电磁阀、气体流量计、油管柱模型、套管模型、固定装置、轴力装置(重量、滑轮)、消声器等,设计了实验台架示意图如图10 所示,并搭建了相应的实验台架(图11)。

图9 实验系统设计流程图Fig.9 Flow chart of experimental system design
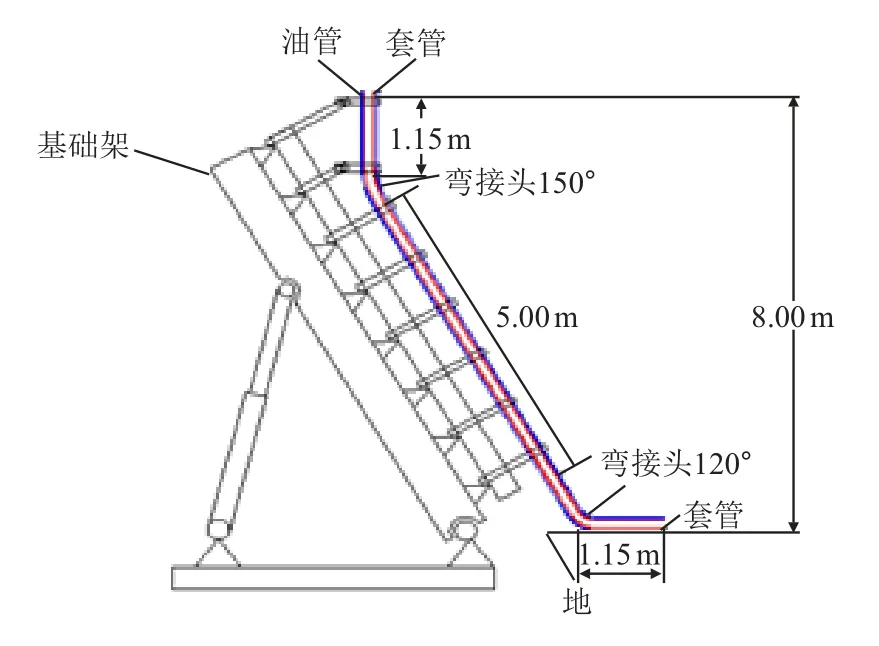
图10 实验台架示意图Fig.10 Schematic diagram of test bench

图11 实验系统实物图Fig.11 Physical diagram of the experimental system
为了采集油管柱的变形特征,在其四周(CF1,CF2,IL1,IL2)分别布置8 个采集点,共计32 个点位,每个点位上横向布置两个应变片,用于温度补偿,消除实验过程中温度、初始变形等误差。实验油管柱采集点1 和采集点8 距两端0.15 m,1∼8 号采集点相邻之间间距1.00 m(如图12 所示)。

图12 应变片安装示意图Fig.12 Diagram of strain gauge installation
2.2.3 实验结果分析
采用本文建立的双重非线性流致振动模型,设置与实验参数一样(表2),计算模型如图13 所示,其中管柱分为300 个单元,模拟总时间为70 s,步长为0.000 1 s,提取了4 个测量点(与实验中安装传感器的位置相同)的振动响应。
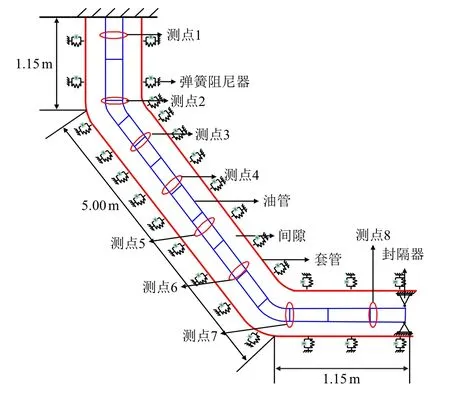
图13 双重非线性流致模型的计算简图Fig.13 Computational sketch of a bi-nonlinear model
图14 为油管不同位置横向振动位移时程曲线,可以看出,通过双重非线性流致振动模型计算和实验测量所得到油管柱横向振动幅值基本一致,两种方法都表明位移响应存在50 s 的瞬态响应,其中,实验结果的高频分量相对较多,主要由于实验环境因素的干扰。图15 为油管不同位置横向振动幅频响应曲线图,由图可知,双重非线性流致振动模型计算的主频率与实验测量结果基本一致,分别为1.4 Hz 和1.6 Hz,管柱在0∼2.0 Hz 的振动能量较大。通过管柱不同测点的时域分析和频域分析,验证了本文所建立的双重非线性流致振动模型的正确性,为中国高产气井管柱安全设计提供了有效的分析工具。
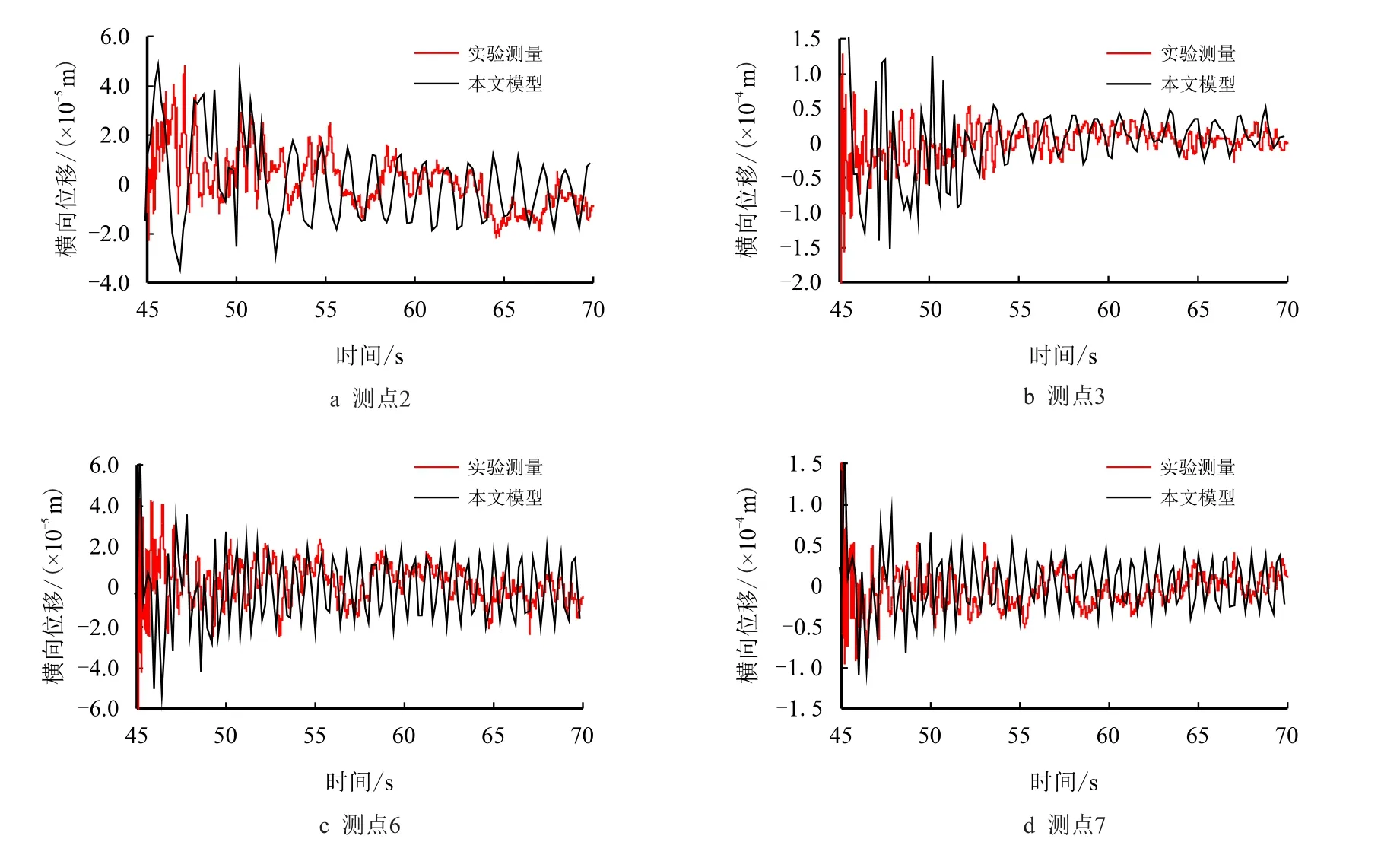
图14 油管不同位置横向振动位移时程曲线Fig.14 Time history curves of transverse displacement at different positions of tubing string
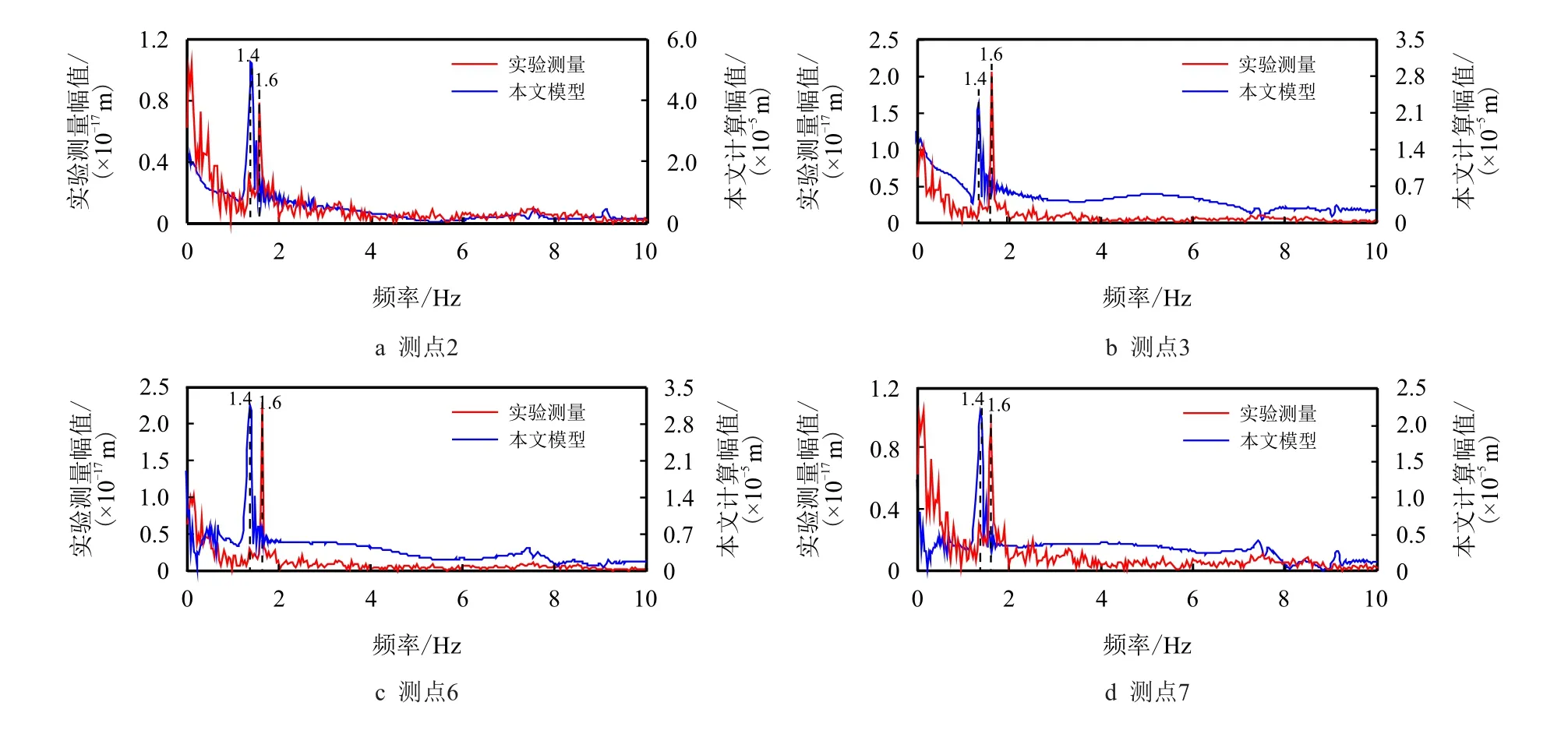
图15 油管不同位置横向振动幅频响应曲线Fig.15 Amplitude-frequency response curve of transverse vibration at different positions of tubing string
3 结论
(1)采用能量法、微元法结合哈密顿原理建立了油管柱纵横向耦合非线性流致振动模型,基于弹塑性接触碰撞理论,建立了油管与套管接触碰撞力和摩擦力计算方法,将其引入油管柱纵横向耦合振动模型中,得到高产气井油管柱双重非线性流致振动模型。
(2)用有限元法和Newmark−β 法求解油管柱的双重非线性流致振动模型,选用文献的实验参数,计算得到油套管接触碰撞力时程曲线,与文献[20]的实验数据和单非线性模型结果对比,本文建立的双重非线性流致振动模型相对于单非线性模型更接近实验数据,初步验证了油管柱非线性流致模型的正确性。
(3)根据现场高产气井参数,采用相似原理,设计了油管柱振动实验方案,搭建了相应的实验台架,开展了高产气井油管柱振动模拟实验,测得实验数据,与理论模型计算结果对比,本文所建立的非线性流致振动模型计算结果和实验测得数据基本一致,进一步验证了模型的正确性。
