基于动态权函数的煤层可压性综合评价
2022-04-23郭大立张书玲王璇甄怀宾王成旺
郭大立 ,张书玲,王璇,甄怀宾,3,王成旺,3
1.西南石油大学理学院,四川 成都610500
2.中国石油煤层气有限责任公司,北京 朝阳100028
3.中联煤层气国家工程研究中心有限责任公司,北京 海淀100095
引言
煤层气作为一种新型的清洁能源,是近二十年来国内外研究的重点[1-2]。水力压裂是煤层气有效开发的主要方法和重要措施,而煤层是否可以进行水力压裂直接影响到企业的生产成本和经济效益。因此,煤层可压性评价是进行水力压裂的重要前提和方法。
煤层可压性是指利用一定的技术和手段,使得煤层压裂裂缝能够形成具有一定长、宽、高,并最终能够实现煤层气井增产上储、产生较好经济效益的评价方法。煤层可压性通常都是利用煤岩地质或测井参数进行定量评价[3-11]。也有很多学者结合室内岩石力学和物性参数测试的方法进行评价[12-17]。范俊佳等从煤岩结构特征对煤层气可采性进行了研究,根据煤储层不同变质变形特征将煤层划分为5类,并通过研究这几类煤储层孔隙结构特征来判断煤层气是否有利于开采[5]。杨聪萍利用主观赋权法、客观赋权法或者两者相结合来确定参数权重,并根据灰色欧几里德加权关联度对可压性参数进行综合评价[8]。郭海萱等通过对岩石的室内力学实验获得岩石抗张强度、抗压强度、抗剪切强度和断裂韧性来评价储层的可压性[12]。赵升等利用煤样的低温液氮吸附回线和压汞实验将煤孔隙类型分为3类,通过分析煤孔隙结构特征对煤层可压性进行了研究[16]。刘光玉等综合岩石的各向异性、脆性、应力敏感性、天然裂缝密度、声发射活动性等共同评价储集层的可压性和造缝能力[18]。赵金洲等通过综合页岩脆性、断裂韧性和天然弱面3 个方面特性,提出了能全面、科学表征页岩气可压性的评价方法[19]。
综上所述,对于煤层可压性的评价主要分为室内物理实验和相关参数综合分析两种方法。前者通过研究煤岩的抗张强度、断裂韧性等对煤岩进行可压性评价,但是该方法需要用到昂贵的设备检测岩石力学参数,成本较高。
相关参数综合评价的方法通常是结合地质或者测井参数进行煤岩可压性评价,但是该方法中权重的设定影响着综合评价的结果。为此,笔者对比了这几种综合评价模型,根据以上模型的优点与不足,引入动态权函数,并对评价对象进行加权冒泡排序来对煤层可压性进行综合评价。不仅对可压性进行了评价,还体现了评价对象在同一类别下产气量的不同差异。
1 煤层可压性参数初选及优选
根据X 区块煤岩煤质特征,得到影响煤层可压性的参数较多,例如声波时差、脆性指数、煤岩抗张强度、煤岩类型、泥质含量、灰分含量、煤岩密度等,本文暂不考虑地层应力场对生产能力的影响。煤岩类型按平均光泽强度可分为光亮煤、半亮煤、半暗煤及暗淡煤4 类。夹矸是夹在煤层之中的其他岩层,夹矸具有较脆且易压裂的特点,对煤层压裂中裂缝高度的动态变化有很大影响,故本文将夹矸视为一种煤岩类型,最终将煤岩类型分为光亮煤、半亮煤、半暗煤、暗淡煤及夹矸5 类。声波时差、脆性指数、煤岩抗张强度以及煤岩密度运用经验公式进行求解[20-28]。其中,煤岩密度采用补偿密度测井结果;泥质含量、灰分含量通过室内物理实验方法获取。
声波时差分为纵波时差与横波时差,本文采用测井参数中的纵波时差,依据实测资料建立的纵波时差与横波时差的经验关系,计算横波时差公式为

结合赵金洲等[19]建立的计算岩石的动态泊松比与动态弹性模量的经验公式,郭炳政[22]通过测井资料进行室内实验和相关算法,优化得到了动态泊松比与静态弹性模量之间的转换系数关系
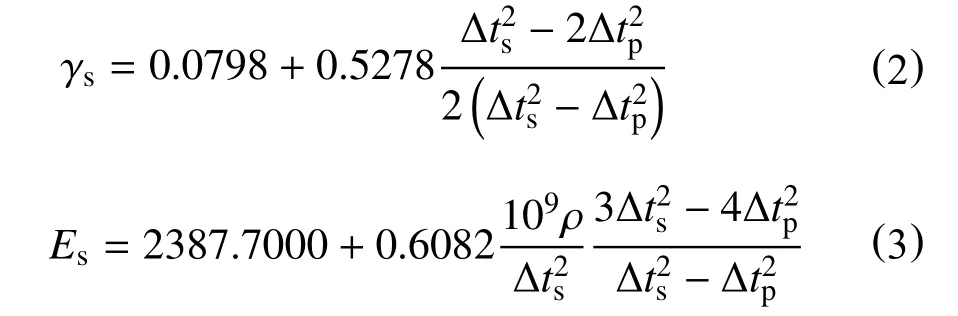
再将静态泊松比与静态弹性模量进行归一化,定义脆性指数

本文采用Miller 和Deere 通过大量实验所建立的单轴抗压强度、黏土含量与弹性模量的关系式求得抗张强度[29]

对收集到的X 区块141 口煤层气井来自同一层段的测井参数,利用数理统计分析的方法,研究了煤层可压性参数与生产能力之间的关系,其中,生产能力的衡量方式为日产量与井底流压的乘积。
数理统计分析表明,声波时差、煤岩密度与煤层气生产能力之间不存在明显的相关性。但大部分参数和煤层气生产能力之间是存在明显相关性的,煤岩灰分含量、泥质含量、抗张强度、脆性指数、煤岩类型与生产能力关系图如图1∼图5 所示。
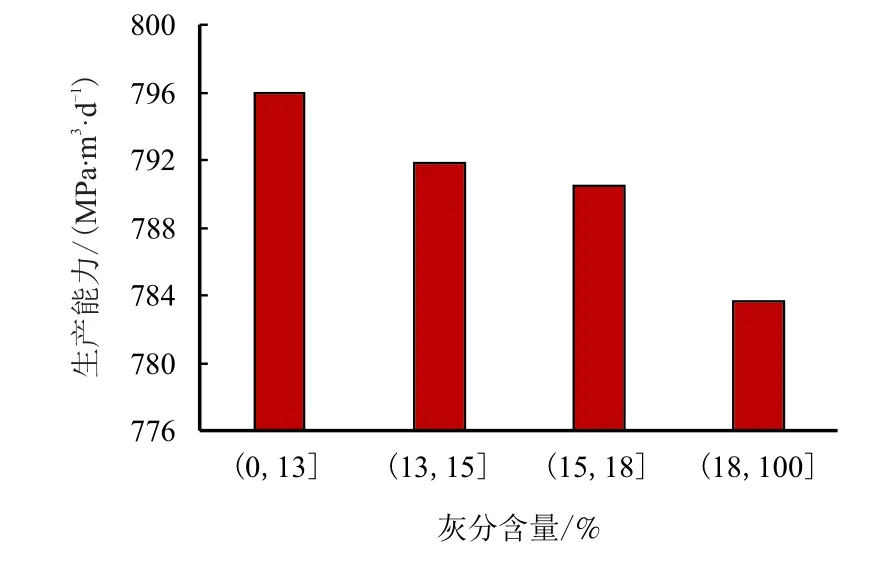
图1 灰分含量与生产能力关系Fig.1 Relationship between ash content and production capacity

图2 泥质含量与生产能力关系Fig.2 Relationship between shale content and production capacity

图3 抗张强度与生产能力关系Fig.3 Relationship between tensile strength and production capacity
由图1∼图5 可见,泥质含量、灰分含量与生产能力呈负相关;煤岩类型、脆性指数和抗张强度与生产能力呈正相关。因此,最终优选出的煤层可压性参数为煤岩灰分含量、泥质含量、抗张强度、脆性指数、煤岩类型5 种。

图4 脆性指数与生产能力关系Fig.4 Relationship between brittleness index and production capacity
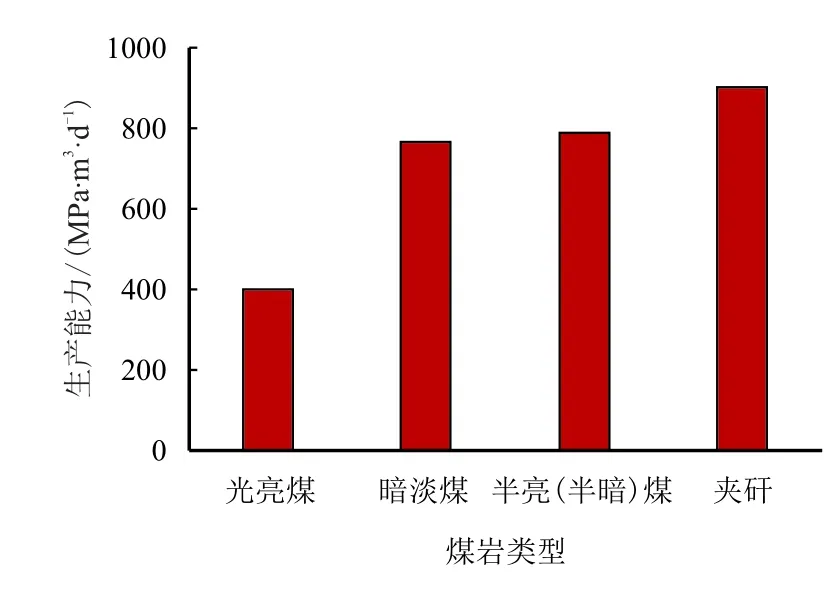
图5 煤岩类型与生产能力关系Fig.5 Relationship between lithotype and production capacity
2 煤层可压性综合评价模型
2.1 评价标准
将煤层气井的生产能力分为低产、中产、高中产和高产4 类。根据生产能力的分类,相应地可以将可压性分为4 类:可压性差、可压性较差、可压性较好和可压性好。根据优选的煤层可压性参数,为了后续方便计算,对煤岩类型进行量化评分。
在煤岩类型中,夹矸在5 种煤岩类型里面产量排名第一,分数为(80,100];根据数理统计方法得到煤岩类型与产量之间的关系如图5,依次对煤岩类型进行赋分,则有半暗煤、半亮煤(60,80];暗淡煤(40,60];光亮煤(0,40]。
根据可压性的分类将优选的参数进行划分。每一个可压性类别对每一项优选的可压性参数都有相应的标准值或者区间,根据生产能力的分类,利用数理统计结果对优选的可压性参数进行区间划分。对煤层可压性进行综合评价时,要充分考虑这些可压性参数标准值不同类别的“质的差异”和同类别的“量的差异”,即属于同一类别的井的产气量存在的差异。
综上,引入动态加权综合评价方法对可压性进行评价,煤层可压性评价标准如表1 所示。

表1 煤层可压性评价标准Tab.1 Evaluation standard of CBM fracability
2.2 S 型分布动态权函数
主观赋权法是决策者根据自身的知识储备以及自身理解对指标的影响程度进行赋权,具有一定的主观性,故对综合评价的结果有一定的影响。客观赋权法虽然是以数学理论为依据,但所得的权重结果存在与事实不一致,甚至对同一个综合评价模型所得权重结果不同的情况。因此,本文引入动态权函数对可压性参数进行赋权,不仅可以科学地对参数进行赋权,还可以体现属于同一类评价对象之间的“量的差异”。
为方便计算,对各可压性参数的评价指标和部分参数进行归一化处理。其中,泥质含量、灰分含量为越小越好型,煤岩类型和抗张强度为越大越好型。对于越大越好型,归一化为

对于越小越好型,归一化为

根据生产能力的分类将可压性分为4类,则有x∈(ak,i,bk,i)(1 ≤i≤m,1 ≤k≤K),根据优选出的可压性参数的趋势可以看出,可压性参数xi对于综合评价效果的影响大约是随着类别的增加而增加的过程,呈一条“S”曲线。故本文建立了优选的可压性参数xi的变权函数,且变权函数设定为S 型分布函数

根据对优选的可压性参数xi进行分析,可看出xi对于综合评价效果大约是随着类别的增加而增加的过程,故可将xi权函数设定为S 型分布权函数。
2.3 基于加权冒泡排序的综合评价模型
本文引入加权冒泡排序法来确定综合排序方案。即在冒泡排序的基础上赋予可压性参数动态权函数,并对其进行排序得到n个评价对象的综合评价结果,即总排序结果。总排序结果可以体现属于同一类评价对象之间的“量的差异”。建立综合评价模型来对n个被评价对象做出综合评价。在此,取综合评价模型为各评价指标的动态加权和,即

由此式的计算结果运用冒泡排序法对其进行升序排列,就可以得到n个评价对象的综合评价结果。
3 实例应用
针对X 区块的煤层气井参数,优选出煤层可压性参数为煤岩抗张强度、煤岩类型、泥质含量、灰分含量和脆性指数等5 种。根据建立的综合评价模型,先对各参数进行归一化,后根据S 型分布动态权函数计算各参数的动态权函数,再根据式(9)得到各评价对象的动态加权和。
根据X 区块的50 口煤层气井的产气量以及优选出的煤层可压性参数,由式(9)计算出相应是动态加权和,对动态加权和与生产能力进行3 次多项式拟合,拟合图如图6 所示。3 次多项式拟合的相关系数R2达到0.864 1,拟合效果较好。说明通过动态加权法计算得到的动态加权和与生产能力有着较好的相关性,生产能力可以用动态加权和进行表征。

图6 动态加权和与生产能力拟合图Fig.6 Dynamic weighted sum and productivity matching
拟合得到动态加权和与生产能力之间的关系式

其中,0 ≤x≤1,R2=0.8641。对比不同多项式次数拟合效果,三次多项式拟合效果较好,且动态权函数与生产能力之间的关系也较符合S 型分布。归一化后的可压性评价标准如表2 所示。
根据ci=0.5(a1,i+bK,i),由于将生产能力分为 了4种,故x∈ (ak,i,bk,i)(1 ≤i≤m,1 ≤k≤4),则根据表2 煤层可压性评价标准,有c1=0.5(a1,1+bk,1)=0.5×(0+1.00)=0.5=c2=c4=c5,c3=0.5(a1,3+bk,3

表2 无因次煤层可压性评价标准Tab.2 Dimensionless evaluation standard of CBM fracability
)=0.5×(0.40+0.67)=0.535。将其代入式(8),可得到5 个优选的可压性参数的权重,由于wi(0.5)=0.5(1 ≤i≤5),则其中4 个优选的可压性参数(i=1,2,4,5)的权重为

根据c3=0.535,故脆性指数的权重为
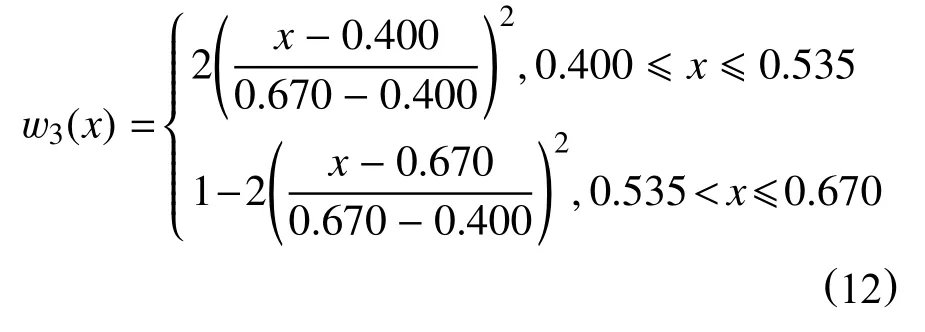
式(12)中,wi(ci)=0.5(1 ≤i≤5)。
利用该模型对X 区块的26 口井进行可压性综合评价,并用加权冒泡排序法来确定综合排序方案,得到的煤层可压性评价结果见图7。

图7 煤层可压性评价结果Fig.7 Evaluation results of CBM fracability
对X 区块26 口井进行可压性评价结果可知,其中3 口井的评价结果错误,可压性评价结果正确率达到88.64%,还可以体现出属于同一类别井的产量存在的差异。该评价方法可对煤层可压性进行有效评价。
4 结论
(1)利用数理统计的方法优选出了影响煤层可压性的主控参数,结果显示,大部分参数与煤层气生产能力之间存在明显的相关性,例如煤岩抗张强度、煤岩类型、泥质含量、灰分含量。其中,泥质含量、灰分含量与产量呈负相关;煤岩类型和抗张强度与产量呈正相关;声波时差、煤岩密度与煤层气生产能力之间不存在明显的相关性。
(2)优选出了5 种煤层可压性参数,其中,泥质含量、灰分含量与产量呈负相关;煤岩类型和抗张强度与产量呈正相关。
(3)引入动态加权综合评价方法对可压性进行评价,给出了煤层可压性评价标准,利用加权冒泡排序法赋予可压性参数动态权函数,建立了综合评价模型。
(4)利用建立的煤层可压性综合评价模型,对X 区块的26 口井进行了评价,可压性评价结果正确率达到88.64%。验证了综合评价模型的准确性。
符号说明

