一种新的计算三元复合驱渗流规律的方法
2022-04-23魏洪涛周庆张虓雷刘忠原
魏洪涛 ,周庆,张虓雷,刘忠原
1.中国石油大庆油田有限责任公司,黑龙江 大庆163712
2.黑龙江省油层物理与渗流力学重点实验室,黑龙江 大庆163712
3.中国石油大庆油田有限责任公司第一采油厂,黑龙江 大庆163712
引言
在水驱开发中,油水相对渗透率曲线是油藏工程计算、油藏数值模拟工作的最基础资料,它的准确度直接影响人们对油田水驱特征的认识以及各种计算准确性,因此,油水相对渗透率曲线的求取是一项非常重要的工作,求取油水两相相对渗透率曲线常用的有稳态法和非稳态法[1-4]。随着三次采油技术的出现,化学驱渗流规律研究对于指导油田在化学驱油开发方向具有重要的作用,因此,研究聚合物相渗曲线、复合驱相渗曲线成为了很多科研人员攻关的方向。2010年,杨清彦等在修正Blake-Kozeny 方程的基础之上推导出了幂律型非牛顿流体驱油的分流量方程、前缘运动方程,并根据推导的驱替前缘运动方程建立了视黏度与注水倍数关系以及平均含水饱和度与末端含水饱和度的关系式,考虑了聚合物溶液稠度系数、幂律指数、不可波及体积、岩石物性以及实验驱替速度等因素的影响,得到了新的聚合物驱相对渗透率计算方法[5-8]。李斌会等通过稳态和非稳态两种测试方法,对聚合物相对渗透率曲线研究进展做了全面的分析和总结,针对存在的问题和不足,通过推导新的理论计算模型和实验方法的改进,给出了相关问题的解决方法[6-9]。随着聚合物相对渗透率曲线计算方法的攻克,很多学者又在复合驱相渗曲线计算方法上进行了探索性研究。由于复合驱体系里面除了含有聚合物,还含有碱、表活剂,它们在储层流动过程中会和储层岩石中的黏土矿物发生物理、化学作用,使得流动黏度是一个变化的量,无法用达西公式来计算复合驱相对渗透率曲线,在推导复合驱相渗曲线的方法上出现了瓶颈[10-12]。本文根据运动方程,将运动方程中的参数团视为一相,即只考虑流度变化,避开了复杂的复合驱物理化学变化过程,推导出了适合复合驱的渗流方程,为解决复合驱渗流规律提供了思路和方法。
1 研究新思路
三元复合驱渗流问题常规研究方法是将JBN方法和有效黏度模型结合[13-16]。ASP 溶液具有类似聚合物流体的黏弹性,属幂律型非牛顿流体,暂时忽略碱和表活剂影响,结合牛顿流体B-K 方程以及圆管层流理论,建立聚合物有效黏度计算模型。聚合物溶液有效黏度计算模型为

将上述有效黏度模型与JBN 方法相结合,有

上述方法在实际应用中存在以下问题:(1)数模软件中无法输入稠度系数、幂律指数,因此,该计算方法无法在数值模拟中应用;(2)有效黏度计算依赖相渗,而相渗计算需提前得到黏度,这是个矛盾的问题,无法计算出来;(3)有效黏度及JBN 方法,计算过程非常复杂,精确度难以保证。
三元复合驱两相相对渗透率计算过程中,复合体系自身及其与岩石、储层流体等将发生复杂的物理、化学反应,导致流体黏度发生变化,进而增大了三元复合驱两相渗流规律的研究难度,这个问题也是困扰研究工作者的一个瓶颈,至今难以逾越[17-20]。但是观察渗流过程中两相流体运动方程式(8)、式(9)可以发现,将运动方程中的渗透率、黏度变化,综合为一个参数“流度”的变化,这样可以将对相对渗透率的研究转换为对流度的研究,如此可忽略驱替过程中两相黏度,以及多孔介质渗透率的变化,将复杂问题简单化。
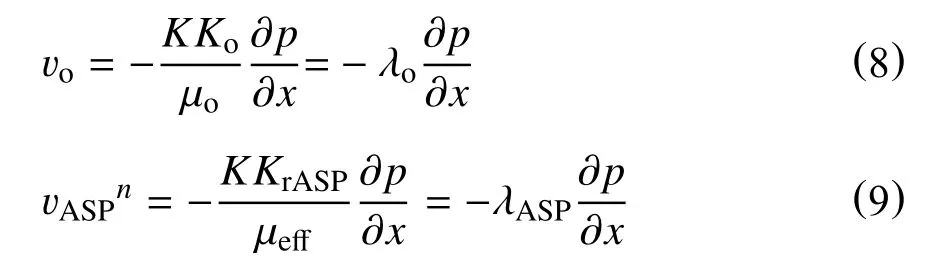
基于以上理论在得到两相流度曲线后,只需将后续渗流规律问题研究,油藏数值模拟等过程中全部将相渗及黏度整体替换为流度即可。
2 三元复合驱驱替实验数据处理新方法
2.1 三元复合驱渗流两相流度计算公式
将运动方程参数团看做一个整体,即引进参数流度,以流度代替相渗的思路来解决复合驱过程中黏度变化问题,将相渗曲线替换为两相流度曲线。因此,本文提出一种新的实验数据处理办法,通过稳态法、非稳态法驱替实验得到两相流度曲线。
两相流度可由相关经验公式计算得到

式(10)和式(11)中的α 和β 为取决于储层岩石孔隙结构和润湿性的两个指数。依照一般经验,它们的取值为2∼4。
2.2 参数拟合
给出a1,a2,α 和β 等4 个参数初始值(a1、a2根据实际测试数据计算,α、β 可根据经验拟定),然后依据复合驱运动方程计算两相流量

得到两相流量后,依据分流方程,即可得到含水率试算值

根据实验实测数据可以得到两相流量、含水率及产液量真实值,对计算值及真实值建立目标函数,进行多目标函数拟合

调整4 个参数值,使得目标函数值最小,即获得较准确的参数值,具体拟合流程见图1。
以某井生产数据为例,按照图1 的流程进行拟合,得到累计产水量、流度关系和含水率拟合曲线,如图2、图3 和图4 所示。
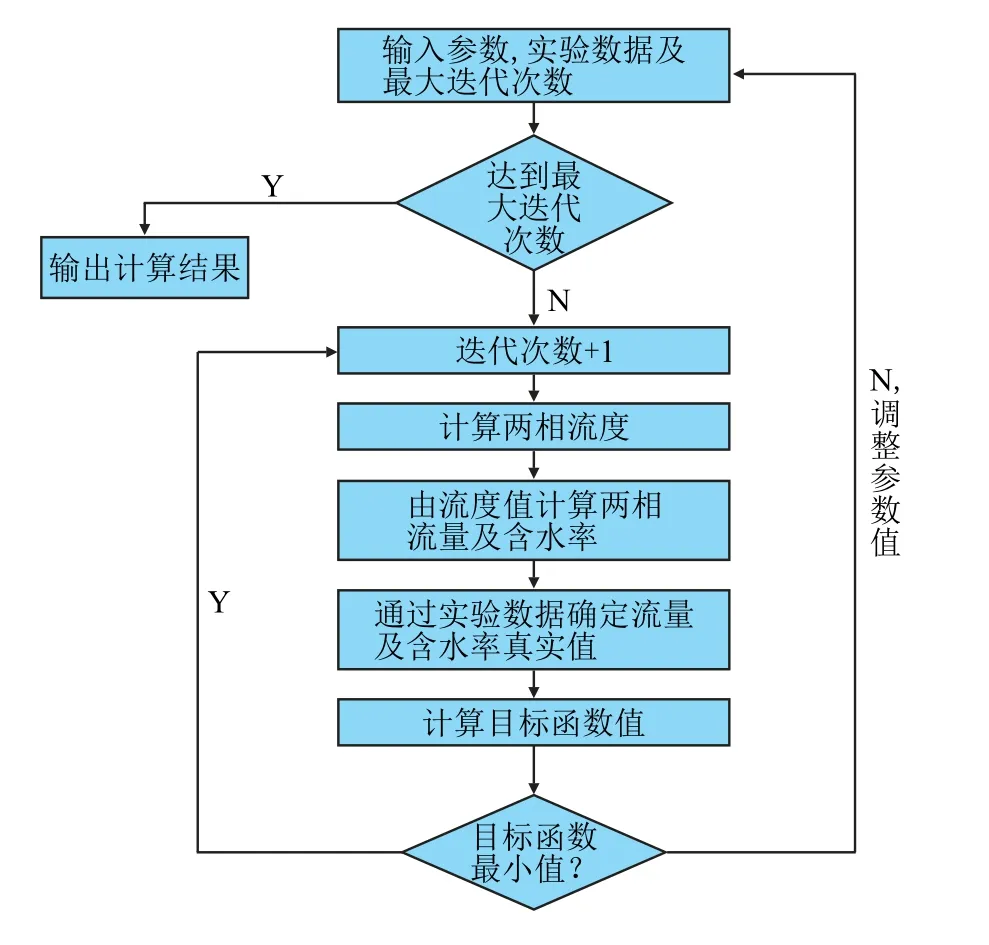
图1 拟合流程图Fig.1 Fitting flow chart

图2 累计产水拟合曲线Fig.2 Cumulative water production fitting curve

图3 流度与含水饱和度关系拟合曲线Fig.3 Fitting curve of relation between fluidity and water saturation
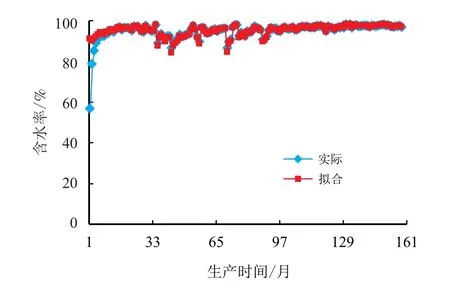
图4 含水率拟合曲线Fig.4 Fitting curve of water content
通过拟合累计产水量、含水率、流度关系结果可以看出,拟合效果较好,可对实验得到流度数据进行有效校正,实验数据拟合法与生产数据拟合法计算得到流度基本相同,说明拟合方法科学可靠。
2.3 无因次采油、采液指数计算
由于将渗透率、黏度变化转换为流度进行研究,因此,将无因次采液、采油指数计算同样转换为流度。
考虑启动压力梯度,根据两相运动方程,无因次采液指数为

不考虑启动压力梯度,无因次采液指数为

不考虑启动压力梯度,无因次采油指数为
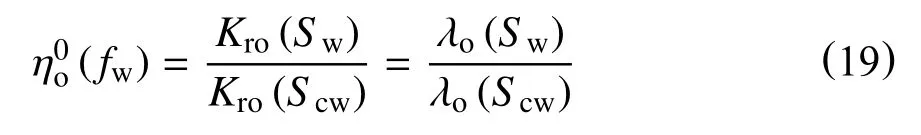
2.4 计算方法可靠性验证
非稳态法水驱实验数据如表1 所示。

表1 非稳态法水驱实验数据Tab.1 Experimental data of water flooding by unsteady state method
为了验证此方法的可靠性,将天然岩芯非稳态法水驱实验结果分别利用JBN 方法和新方法数据处理结果进行对比,两种方法绘制的流度-含水率曲线如图5 所示。
由图5 可见,两种方法计算出来的实验结果基本吻合,说明该方法可以计算并处理驱替实验数据,具有一定的可靠性。

图5 JBN 方法与新方法处理结果曲线对比图Fig.5 Curve comparison between the JBN method and the new method
3 新方法的应用
利用新方法处理了大量的三元复合驱实验数据,仅以3 块岩芯的处理结果为例,表2 是这些岩芯的关键参数。

表2 三块岩芯关键参数表Tab.2 Key parameters of 3 cores
实验采用的三元复合驱体系为弱碱三元复合体系,聚合物为普通聚合物,分子量为1 200万,浓度1 900 mg/L,黏度为30 mPa·s,表面活性剂为石油磺酸盐,碱为弱碱Na2CO3。
实验过程为将岩芯饱和地层水后,饱和模拟油层束缚水,然后以恒定的速度进行水驱油,当含水率达到98%后,注入0.2 PV 聚合物,0.3 PV 的弱碱三元复合体系,再进行后续水驱。
图6 和图7 分别为样品33–3 用流度表示的油水变化曲线和含水上升率曲线。由该样品的流度变化曲线来可见,油相流度下降缓慢,复合驱流度上升平缓,两相共存范围小,见水后,含水率上升的较快,说明样品33–3 见水之前驱油效果较高,见水后产油量较少。

图6 样品33–3 用流度表示的油水变化曲线Fig.6 Oil-water change curve expressed by fluidity of sample 33–3

图7 样品33–3 含水率变化曲线Fig.7 Water content change curve of sample 33–3
图8 为样品33–3 的无因次采液、采油指数随含水率变化曲线。

图8 样品33–3 无因次采液、采油指数变化曲线Fig.8 Fluid extraction and oil production index change curve of sample 33–3
由图8 可见,随着含水率增加,无因次采液指数、采油指数都呈现递减趋势,且前期递减幅度较大。说明见水后,产油量骤降,产水量增加。
样品16–2 的流度变化曲线见图9,含水上升率曲线见图10。由图9 和图10 可见,油相流度下降较快,复合驱流度上升平缓,两相共存范围小,见水后,含水率上升的较快。说明了样品16–2 见水前后驱油效果都不是很理想,见水后出油较少。

图9 样品16–2 用流度表示的油水变化曲线Fig.9 Oil-water change curve expressed by fluidity of sample 16–2

图10 样品16–2 含水率变化曲线Fig.10 Water content change curve of sample 16–2
图11 给出了样品16–2 的无因次采液、采油指数随着含水率变化曲线。

图11 样品16–2 无因次采油、采液指数变化曲线Fig.11 Fluid extraction and oil production index change curve ofsample 16–2
由图11 可见,随着含水率增加,无因次采液指数、采油指数都呈现递减趋势,前期递减幅度和样品33–3 相比同样较大。也说明了见水后,产出油量骤降,产水量增加的问题。
样品11–1 流度曲线见图12,含水上升率曲线见图13。由图12、图13 可见,油相流度下降缓慢,复合驱流度上升快,两相共存范围与前两块岩芯相比较大。见水后,含水率上升的较快。说明了样品11–1 见水前驱油效果较好,见水后水相流度上升快,产油量减少。

图12 样品11–1 用流度表示的油水变化曲线Fig.12 Oil-water change curve expressed by fluidity of sample 11–1

图13 样品11–1 含水率变化曲线Fig.13 Water content change curve of sample 11–1
图14 给出了样品11–1 无因次采液指数、采油指数随着含水率变化曲线。由图14 可见,随着含水率增加,无因次采液指数、采油指数都呈现递减趋势,前期递减幅度也较大,也说明了见水后,产出油量减少,产水量增加。

图14 样品11–1 无因次采油、采液指数变化曲线Fig.14 Fluid extraction and oil production index change curve of sample 11–1
综合来看,3 块岩芯属于同一渗透率级别天然岩芯,样品33–3 与样品16–2 油相流度、水相流度与含水率关系变化趋势差别不大,随着含水率增加,水相流度增加缓慢,油相流度下降也相对缓慢;而样品11–1 随着含水率增加,水相流度上升速度加大。含水率与含水上升率关系来看,样品33–3、样品11–1 随着含水率增加,含水上升率缓慢增加,而样品16–2 含水上升率增加较快。含水率达到70%以上后,样品33–3、样品11–1 含水上升率达到峰值,样品16–2 当含水率达到5%的时候,含水上升率就已经达到了峰值。
从3 块岩芯结果来看,三元复合驱水相流度始终较低,说明三元复合驱能有效降低水相流动能力,但从采液指数来看,三元复合驱采液指数持续下降,后期提液困难。
4 结论
(1)以流度变化代替复合驱过程中黏度变化的思路,避免了三元复合驱渗流过程中复杂的物理化学变化的影响,简化研究过程,为求取三元复合驱渗流特征曲线及相关参数提供了科学合理的方法。
(2)通过拟合累计产水量、含水率、流度关系结果可以看出,拟合效果较好,可对实验得到流度数据进行有效校正,实验数据拟合法与生产数据拟合法吻合较好,拟合方法科学可靠。
(3)三元复合驱能有效降低水相流动能力,但从采液指数来看,三元复合驱采液指数持续下降,后期提液困难,所以,三元复合体系的优化和筛选显得尤为重要。
符号说明


