小题压轴、例析数列计数问题的几个思路
2022-04-23王永军
王永军
(重庆市广益中学校,重庆 400065)
填空题在高考数学试题中具有承前启后的作用,一般前承选择题、后启解答题,个别填空题还具有“压轴大题”的功能,想要“解答”清楚并非易事。数列中的计数问题是数列的基本的、核心的问题,数列的项数问题是数列求和的前期问题。本文主要结合近几年的高考数学试题中数列填空题中的计数问题,给出三个求解思路。
一、常规方法,直接感知
列举、写出数列的前几项,直接感知数列的通项公式,是计数问题的最基本、最常规的方法。
例题1(2020年高考新高考卷) 将数列{2n-1}与{3n-2}的公共项从小到大排列,得到数列{an},则{an}的前n项和为_______。
解析 分别写出数列{2n-1}与{3n-2}的前几项,发现公共项为1、7、13、19,……,于是可以猜测数列{an}是以1为首项、6为公差的等差数列。
an=1+(n-1)·6=6n-5,


综上所述,A=B,猜测正确。这样的推理过程在考试中是不允许的(主要是时间不允许、没时间),也是没有必要的。但是在平时的训练中应加强练习,增加对数列推理的一些感性认识,提升数学学习的兴趣[1-2]。
二、估算逼近,合情推理
一些看似简单的数列,要想精确的求解,需要对数列的项数不断进行“逼近”,要对项数进行合理、充分地估算,以合情推理达到求解的目的。
例题2(2018年高考江苏卷) 已知集合A={x|x=2n-1,n∈N*},B={x|x=2n,n∈N*},AB中的所有元素按从小到大的顺序依次排列构成一个数列{an}。记数列{an}的前n项和为Sn,则使Sn>12an+1成立的n的最小值为______。
解析 数列{an}的前几项是容易列举的,但本题是一个非常复杂的数列计数问题。
答案:27。
我们可以很容易写出数列{an}的前10项、前20项,而且数列中自然数排列的规律也很明显。现在采用估值逼近的办法对本题进行精致的求解[3-4]。
第一步,易见数列{an}是严格单调递增数列。
又a12=24=16,a13=17,欲使Sn>12an+1成立,则n≥13。
而12a14-S13=117,a17=25,4a17<117,故n≥17。
第二步,现用数学归纳法证明:若存在n(n≥17),使Sn>12an+1成立,则Sn+1>12an+2,即n+1也使不等式成立。
事实上,易见an+1>24≥(an+2-an+1),
于是Sn+1=Sn+an+1>13an+1>12an+2。
这表明,若Sn>12an+1,则使其成立的n的最小值是存在的。
第三步,估算、逼近区间。
注意到a21=25=32,
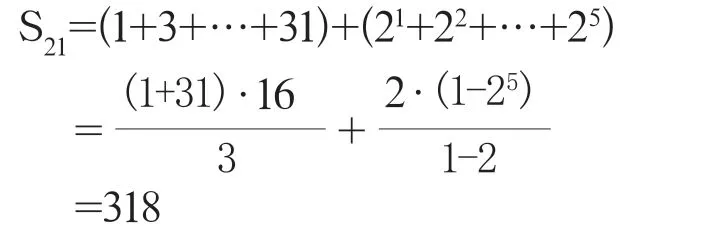
而12a12=12·33=396>318,故n>21。
类似地,a38=26=64,S36=1023>756>12a37。
下面考虑21<n≤36。
第四步,精准求解。
Sn=(1+3+…+2(n-5)-1)+(21+22+…+25)
=(n-5)2+(26-2)
>12an+1=12(2(n-4)-1)
整理得,n2-34n+195>0,
本题为了求和,对数列进行了细致地研读,合理分段、合情推理、步步逼近,以期达到精准计数的目的。
三、回归过程,生成有据
生活中很多有趣的手工活动为数列的应用提供了广阔的舞台,它们有的是我国古老的民间艺术、是我国传统文化的瑰宝、是非物质文化遗产,有着丰富的历史文化信息。

解析 本题折纸过程是清晰的,第一空用列举法,不难。第二空需要找到“数列的通项”,很难,体现了高考“压轴大题”的本色。
答案:5;720-15(n+3)·24-n
在求解第一空时用列举法会发现图形的“重复”,比如对折2次,会出现2次10dm×6dm规格的图形,但最后种数只算1次。随着对折次数的增加“重复”次数也会增加。这个计数必须搞清楚,否则Sn无法计算,求和就更无从谈起[5]。
无序的列举是繁杂的、徒劳的。要搞清楚计数问题,必须回归折纸的过程,看看“新”的矩形到底是如何产生的。
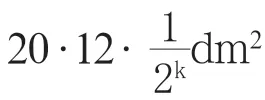
这样,对折后的小矩形好像有k+1种。问题是这k+1种小矩形有没有“重复”的?下面证明恰好有这么多。
显然,



重视数列的生成和发展,抽象、化归为常见的数列模型是处理数列问题的重要思想方法。注重在知识点的“交汇”处处理问题。补例4是数列与三角函数的交汇与融合,很好地考查了数学的应用意识,是值得关注与研究的考试试题题型。
四、备考反思
常规的列举法是考查数列中计数问题的最重要、最基本的方法。由列举而猜测数列的“通项”,仅此猜测对于考试中的填空题解答来说好像已经足够了。作为平时的练习作业,“先猜后证”是重要的数学学习方法(学习态度),也是科学研究的重要方法。“证”得多了,“猜”才有感觉、才有顿悟,可以减少盲目性、多一份自信。毕竟学习要知其然,更知其所以然。
