基于NSST变换的超声图像降噪算法

蒲久亮 高小明

(西南科技大学计算机科学与技术学院 四川绵阳 621010)

医学超声成像技术具有无创性、低成本、安全性高、实时成像[1-2]等优点，是医学诊断领域中应用最广泛的成像技术之一，适用于各个年龄段的人体病理检查。然而，由于反向散射回波信号的影响[3]，导致了超声图像受到斑点噪声的影响，降低了图像的对比度，影响了图像的质量。为了通过超声图像获得可靠的病灶诊断和分析，对斑点噪声的抑制是必不可少的。

超声图像去噪算法主要分为基于空间域去噪方法和基于变换域去噪方法。空间域滤波器直接作用于图像，因此其去噪效果由局部窗口中相邻像素点的统计特性所决定。文献[4]结合各向异性扩散和斑点噪声的特点提出了散斑减少各向异性扩散滤波器(SRAD)。文献[5]提出了挤压盒过滤器(SBF)，能在每次迭代中去除异常值。文献[6]基于光学相干断层扫描图像的特性提出了改进的自适应加权双边滤波器，保持图像的纹理特征。文献[7]结合全变差和高阶全变差的优点，优化了全变分正则化模型，在降低噪声的同时减少了梯度伪影。空间域去噪算法虽然时间复杂度低，但是会造成图像模糊，导致图像小信号丢失。基于变换域去噪算法利用了图像在变换域中的特性来降低噪声。文献[8]根据斑点噪声的分布特点提出了一种新的正交小波族。文献[9]为了克服传统小波对不连续多维信号处理效果不佳的问题，提出了离散剪切波变换的系数方向图像表示方法。虽然变换域能够有效提取图像的细节信息，但是传统的阈值处理方法会导致变换域系数出现不连续性和恒定偏差。

结合空间域和变换域的特点，笔者提出了一种改进的基于NSST变换的超声去噪算法。首先对噪声图像进行对数变换，然后利用NSST变换分解噪声图像得到低频子带和高频子带，低频子带采用同态滤波，高频子带使用改进的阈值处理函数减少噪声，接着对处理之后的高频子带采用梯度域引导滤波器，增加图像的细节信息和对比信息，最后再将逆NSST变换得到的图像进行指数变换得到最终的去噪图像。

1 非下采样剪切波变换

在众多学者的研究中，将大量的多尺度分解方法应用于图像去噪领域，相比于其他多尺度分解方法，非下采样剪切波变换(NSST)在避免伪吉布斯现象出现的同时保证了多尺度分解的效率[10]。

NSST变换是对剪切波变换的进一步改进。在剪切波变换中将复合膨胀仿射变换作为基函数，简化了计算过程，实现了图像的多方向信息表达[11]。当图像为二维时，复合膨胀的仿射变换系统表示如下：

(1)

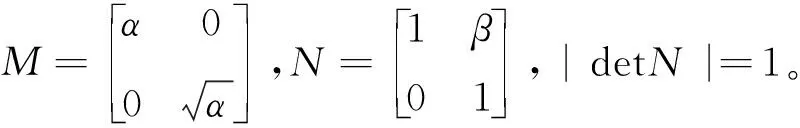
NSST变换相比于剪切波变换具有平移不变性和更好的方向性[12]。NSST变换采用二维卷积运算替代伪极化网格系统，避免了二次采样的过程，保证了平移不变性。NSST分解的离散化过程包括利用非下采样拉普拉斯金字塔(NSLP)实现多尺度分解从而获得高频子带和低频子带，通过剪切波滤波器(SF)实现方向定位。图1显示了NSST的多尺度和多方向分解，图中显示了3尺度分解，在尺度为1，2和3时确定的方向参数分别为16，8和4。

图1 NSST多尺度多方向分解Fig.1 Multiscale and multidirectional decomposition of NSST

在对图像进行多尺度和多方向分解的过程中，分层层数对图像的降噪效果影响很大。如果分层层数过少，就无法准确分离图像的高频信息和低频信息，低频部分会存在大量本属于高频部分的信息，降低降噪效果。如果分层层数过多，虽然可以得到更为细致的细节信息，但是阈值函数的确定将会变得十分复杂，同样不利于图像降噪的实现。因此，本文将分层层数设为4层。

2 算法设计思路及原理

首先对噪声图像进行对数变换，将乘性噪声转换为加性噪声，然后对图像进行NSST分解，得到高频子带和低频子带，对高频子带和低频子带采用不同的处理方式。经过对数变换和NSST变换的低频子带的轮廓信息和细微的边缘信息是线性可分离的，利用同态滤波的性质对低频子带进行增强。高频子带根据超声图像的特征和对数变换的特点改进了阈值函数和收缩函数，避免传统方式出现的不连续性和恒定偏差，对处理之后的高频子带进行梯度域导向滤波变换，对阈值处理之后的子带进行补偿，增加子带的细节信息。得到所有处理之后的子带后，进行逆NSST变换，再进行指数变换，即可得到最终的去噪图像。去噪框图如图2所示。

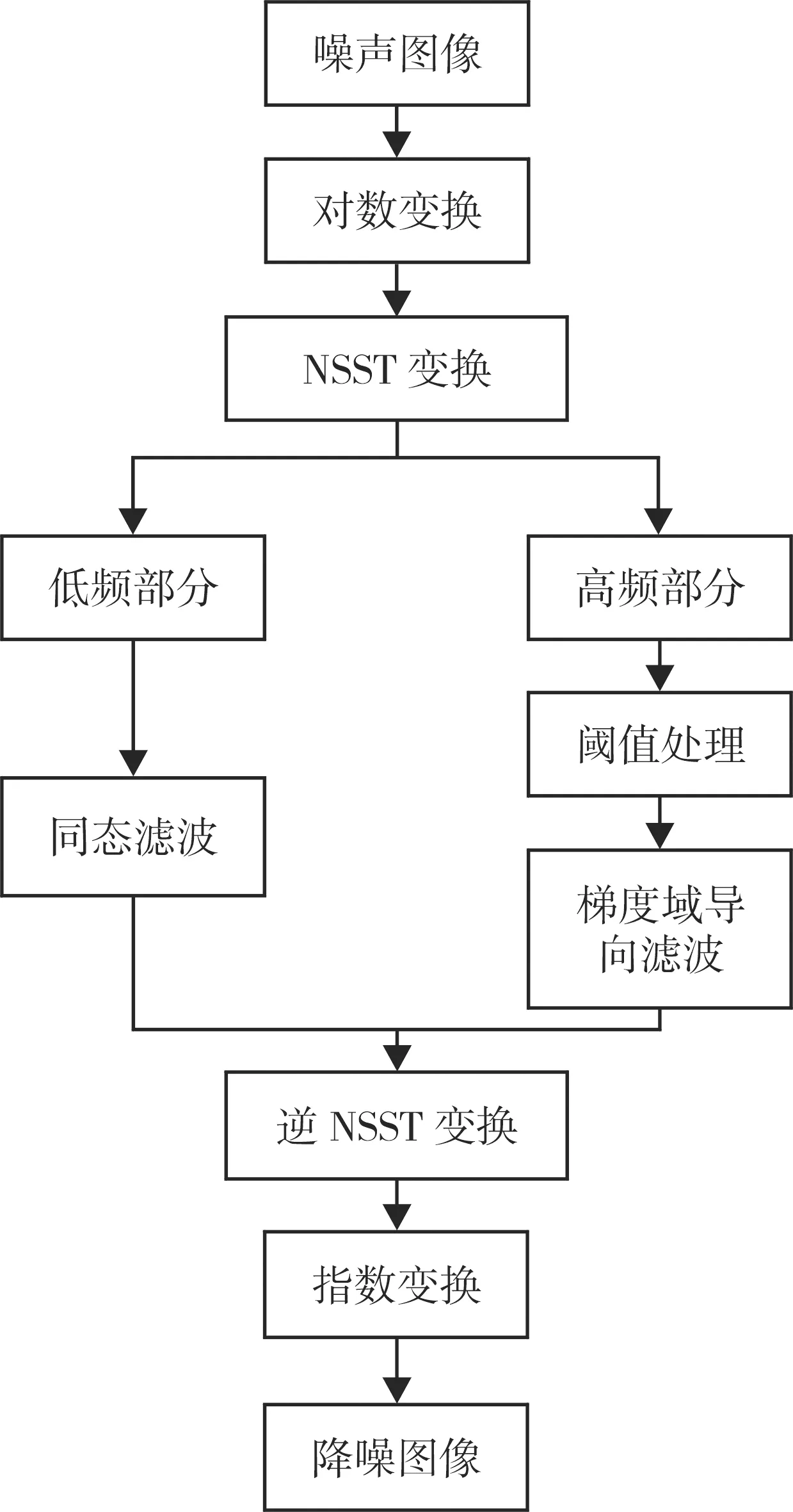
图2 整体去噪框架Fig.2 Integrated denoising framework

2.1 斑点噪声模型

斑点噪声是在超声成像过程中由于散射回波信号之间的相互影响而产生的。相对于乘性噪声，加性噪声对超声图像的影响较小。因此，斑点噪声的模型可表示为：

O(x,y)=I(x,y)×ω(x,y)

(2)

其中：O(x,y)表示含有噪声的超声图像；I(x,y)和ω(x,y)分别表示无噪声图像和乘性斑点噪声。利用对数变换将乘性噪声转换为加性噪声。其中log(ω(x,y))可以近似为高斯加性白噪声。

log(O(x,y))=log(I(x,y))+log(ω(x,y))

(3)

2.2 基于同态滤波的低频处理

普遍认为低频子带主要包含图像的轮廓信息，传统的变换域去噪方法忽略了对低频子带的处理。但文献[13]研究发现，变换域的低频子带同样存在噪声和边缘信息。故本文提出了一种基于同态滤波的低频子带处理方法，表达式如下：

N(x,y)=J(x,y)×L(x,y)

(4)

其中：L(x,y)为经过对数变换和NSST变换的低频子带；J(x,y)是同态滤波函数，其值直接影响变换计算结果的准确性。使用式(5)对同态滤波函数进行取值：

J(x,y)=(rH-rL)×(exp(c×

(5)

其中：rH和rL分别表示高频增益和低频增益，为了只增加低频子带的边缘信息，rL取值为1；c用于调节滤波器函数斜面的锐化，c∈[rL,rH]；D0是停止过滤的频率；D(x,y)表示点(x,y)到NSST变换最初点的距离。

D(x,y)=(x-W)2+(y-H)2

(6)

W和H分别表示低频子带的长和宽。

2.3 改进的阈值函数和收缩方程

通过NSST变换得到的高频部分包括了图像的边缘信息和噪声，为了降低图像的噪声，需要选择合适的阈值滤除噪声信息同时保留边缘信息。在对阈值算法的研究过程中发现：Level Shrink阈值函数解决了统一阈值的问题，为阈值算法的改进提供了依据；基于贝叶斯收缩阈值函数解决了信号统计的自适应参数选择问题。鉴于上述方法的优点，结合超声图像的特征以及NSST变换的多尺度和多方向性，提出了一种改进的阈值函数T。

(7)

其中：j(i=1,2,…J)表示NSST变化的分解层数，J是最多的分解层数；aj表示第j层的自适应参数aj=ln(j)；M表示剪切波中剪切波系数Aj,k的数量；δn和δw,j分别表示无噪声图像的标准偏差和噪声图像的标准偏差，δn根据高频子带的每层剪切波系数Aj,k的中值取得，δw,j由当前层的剪切波系数所决定。

(8)

(9)

图像经过NSST变换之后的结果就是剪切波系数，剪切波系数是没有量纲单位的结果，重构之后才能得到实际有量纲的信号。

传统的阈值收缩方法包括利用剪切波系数进行软阈值收缩和硬阈值收缩，分别如式(10)和式(11)所示：

(10)

(11)

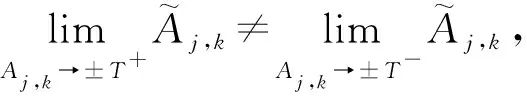
(12)

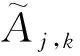
上述收缩函数避免了软阈值出现的恒定偏差，当Aj,k→+∞时：

(Aj,k-Aj,k)=0

当Aj,k→-∞时：

(Aj,k-Aj,k)=0

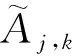
2.4 梯度域引导滤波

通过阈值处理可有效降低图像噪声，但同时会导致部分信息丢失，在文献[14]中已论证了可将梯度域引导滤波应用于单幅图像以实现细节增强。因此，对于同样可视为单幅图像的高频子带，亦可应用梯度域引导滤波，以保留高频子带中的边缘细节。

基于一阶边缘感知的梯度域引导滤波是在引导滤波的基础上改进的算法，要求输出图像与引导图像具有线性关系，可以表示为：

qi=ahGi+bh

(13)

其中(ah,bh)是以h为掩模尺寸的正方形窗口ωh中的线性系数。为了确定最佳线性系数(ah,bh)，文献[14]在构造的能量方程中取最小值作为最佳线性系数：

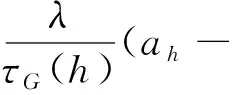
(14)

其中：pi是待滤波图像；λ是正则化参数，值越大滤波强度越大，反之越小;τG是基于GDGIF的一阶的边缘感知权重，图像的边缘由于边缘感知权重的存在得到了更好保存。

(15)

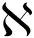
(16)

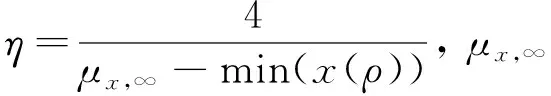
ah1和bh1的优化值可转换为式(17)和式(18)：

(17)

bh1=μq(h)-ahμG(h)

(18)

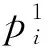
(19)

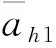
3 算法评估

3.1 评估参数指标

为了客观验证所提出算法的有效性和适用性，将峰值信噪比(PSNR)和结构相似度(SSIM)作为图像质量的评价指标[15]。

PSNR可以用于评价灰度图像噪声的抑制效果，PSNR的值越大表示算法的噪声抑制效果越好。

(20)

其中MSE表示的是均方误差。

(21)

其中：G表示原始超声图像；H表示去噪之后的超声图像。

SSIM用于预测去噪图像中结构内容的保留情况。SSIM的值介于0到1之间。SSIM越接近1表示去噪之后的图像与原始图像有更高的相似性。

(22)

其中：λx，φx，λy，φy和φxy分别表示降噪图像x的均值和标准差、参考图像y的均值和标准差以及协方差。

3.2 去噪效果评估

为了验证本文算法的有效性，对大量图像样本进行了实验，这里选用了人体肝脏超声图像、人体子宫超声图像和人体胆囊超声图像处理结果进行展示。以上实验均在MATLAB R2016R进行仿真实验，操作系统为Windows 10，CPU为AMD A8-6410，内存8 G。将本文算法与SRAD算法、NSST去噪算法及文献[3]、文献[6]、文献[7]的算法进行了对比。图3、图4、图5是不同算法的降噪结果。

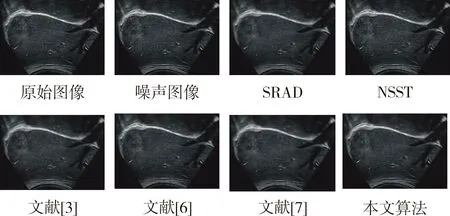
图3 肝脏超声图像降噪效果对比Fig.3 Comparison of noise reduction effect of liver ultrasound images

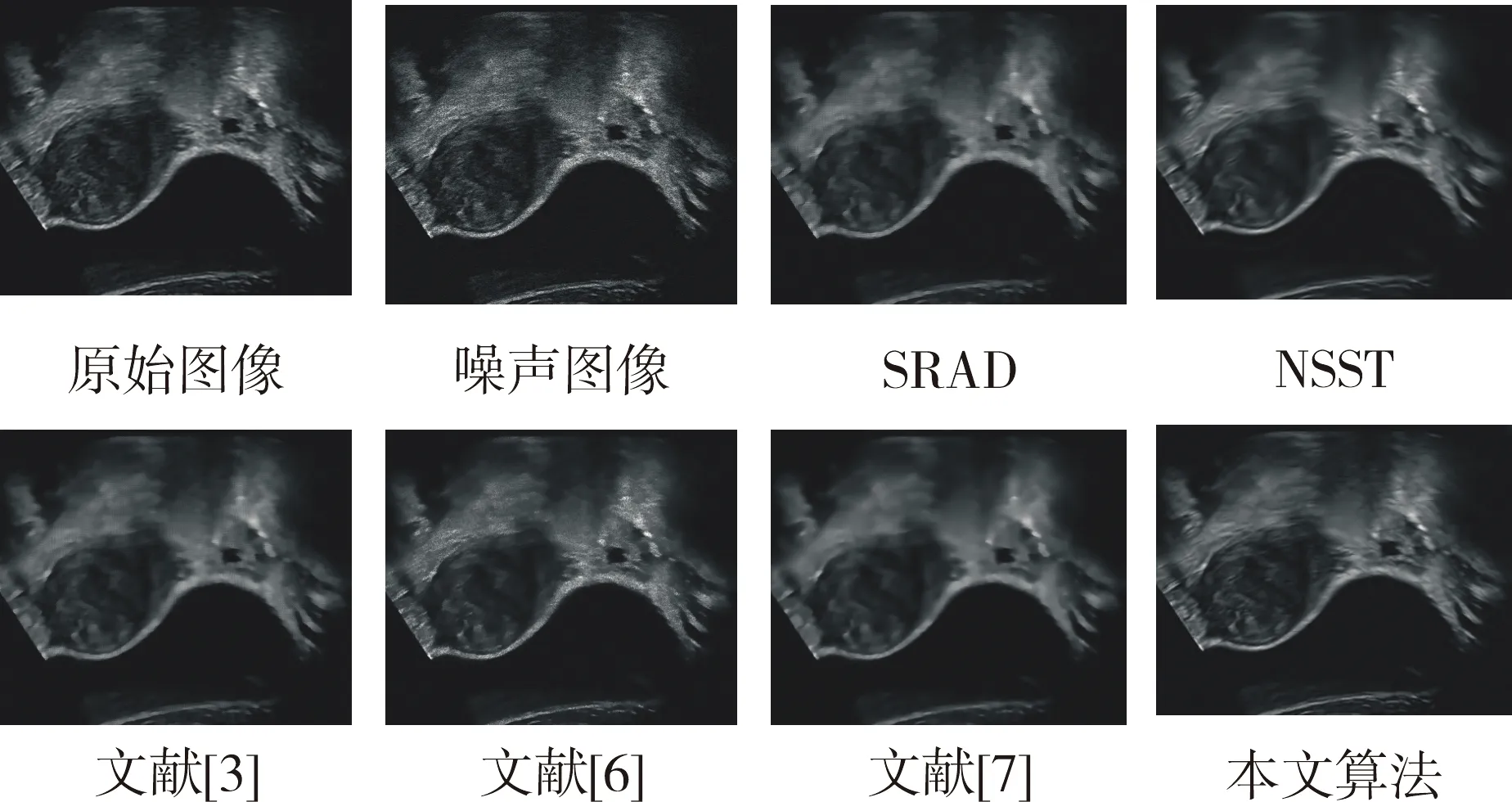
图4 子宫超声图像降噪效果对比Fig.4 Comparison of noise reduction effect of uterine ultrasound images

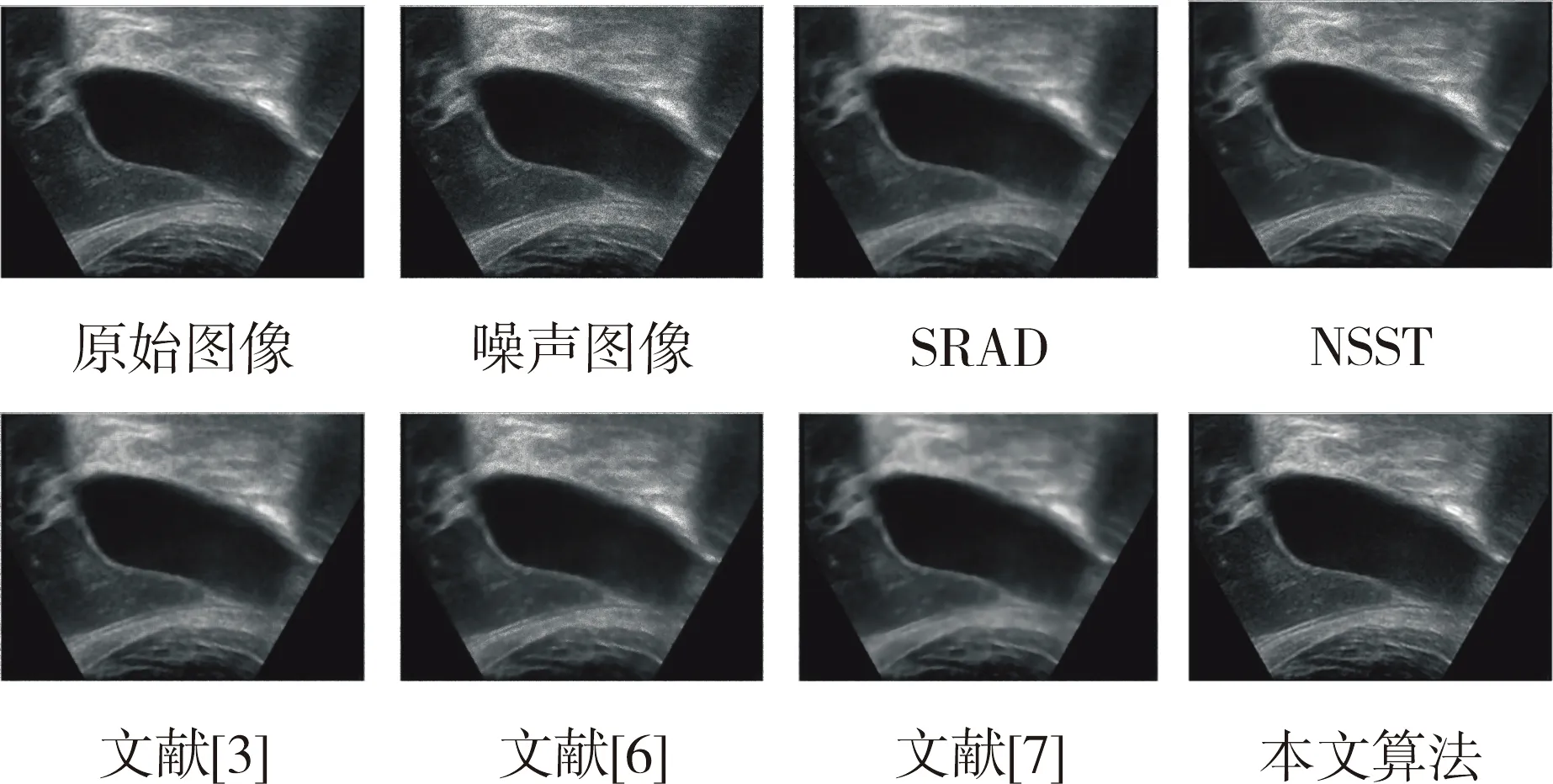
图5 胆囊超声图像降噪效果对比Fig.5 Comparison of noise reduction effect of gallbladder ultrasound images

经过试验对比发现，几个降噪算法在不同程度上降低了超声图像的噪声。但是，从细节上看，由于SRAD和文献[3]的算法对噪声图像区域划分过于简单，造成强边缘和孤立边缘损失。文献[6]的算法虽然保留了大部分的细节信息，同时也保留了许多斑点噪声，NSST降噪采用了统一的阈值，在降低图像噪声的同时，产生了许多伪边缘，文献[7]的算法解决了全变分降噪的阶梯伪影，但是图像整体模糊，对比度低。从本文所提出的算法可以发现，本文算法平衡了降低噪声和保留细节信息，并且提高了图像的对比度。在改善视觉效果的同时没有改变图像的信息分布。为客观评价算法的性能，表1、表2、表3、表4展示了各种算法处理后的PSNR和SSIM性能指标。可以发现，本文所提出的算法在PSNR和SSIM性能上相比于其他算法有所改善。这说明改进算法能够在降低噪声的同时保留图像的细节信息，提高图像的对比度。

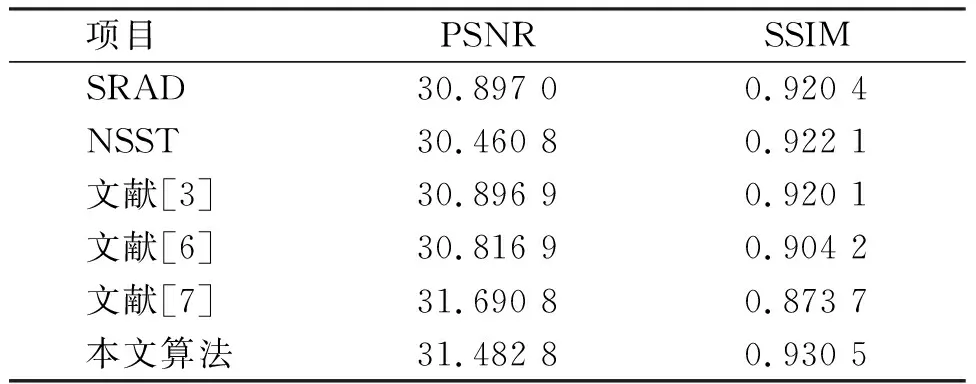
表1 图3各算法评价指标Table 1 Evaluation index of each algorithm in Fig.3

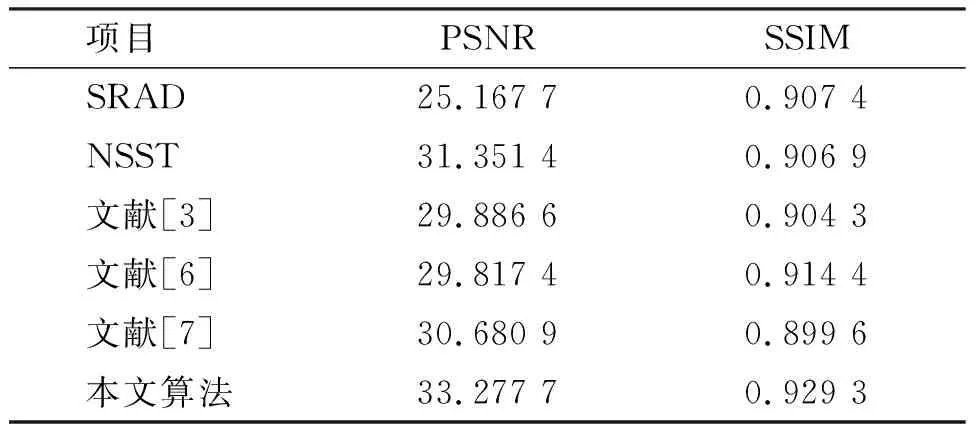
表2 图4各算法评价指标Table 2 Evaluation index of each algorithm in Fig.4

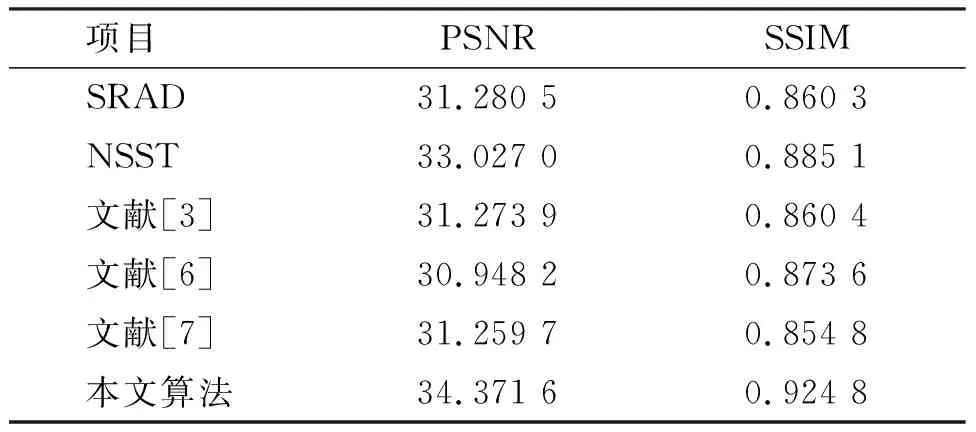
表3 图5各算法评价指标Table 3 Evaluation index of each algorithm in Fig.5

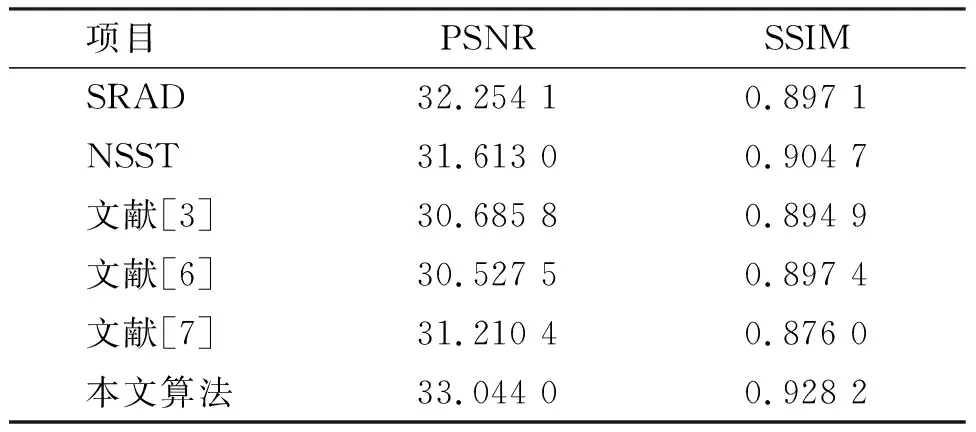
表4 各算法平均评价指标Table 4 Average evaluation index of each algorithm

4 结论

针对当前超声图像去噪算法在去噪的同时存在图像细节信息丢失的问题，提出了一种改进的基于NSST变换的超声图像降噪算法。该算法利用了NSST变换将图像分解为高频和低频部分，低频子带采用同态滤波的方式增加细节信息，根据对数变换的特征和超声图像的特征改进阈值函数和收缩函数，通过GDGIF补偿了由于阈值去噪丢失的边缘信息。实验发现，本文算法的峰值信噪比和结构相似度有一定提升，提高了去噪图像的质量，能在降低超声图像噪声的同时保留图像的细节信息。