粤东地区降水量空间插值方法研究

曾广建

(广东省水文局汕头水文分局，广东 汕头 515041)

降雨是研究流域或地区水文循环系统的关键要素，对于工农业生产、水利开发、江河防洪和工程管理等方面作用很大，降雨量的多少直接影响到人类的生产和生活。受地形地貌、技术手段、财力等因素限制，大部分地区空间位置上的雨量数据是无法实测获取的。根据已有的地面离散站点的降雨数据，选择合理的空间插值方法得到整个区域的降雨空间分布是研究者探索的热点[1-6]，如房林东等研究了反距离权重插值法在贵州西部地区插值分析，得出在山区、平原混合地形区，普通的反距离权重插值法精度较高[1]；王旭等研究了自适应距离的反距离权重法，并在滦河流域进行了应用[2]；吴晓燕等应用5种插值方法对新疆天山山区降雨量进行分析，得出西部复杂山区考虑地形因素的协同克里金法最优[3]；庄立伟等对东北降雨量数据进行空间插值方法比较，认为IDW插值方法优于克里金插值法[4]。

已有研究表明[4-7,11]，由于研究区域、数据集、时间尺度等的差异，不同的插值方法适应性不同，无普遍适用的插值方法和固定的参数取值。大多数研究者在平坦内陆地区或者中等尺度的复杂山区进行分析，在沿海地区进行分析的较少，而粤东地区地势北高南低，西北部和东北部主要是山地丘陵地带，平原主要分布在南部和东南部沿海地带，这种复杂的地形及沿海气候特征，受地形因子、气候多变、技术手段和现有站点数目少等多种因素的限制，致使对粤东地区降雨空间分布特征的认识不完整，制约了该地区与降雨规律相关的各种水文分析研究，因此积极探索一种适用于粤东地区的降雨插值方法是必然的、迫切的。本文以粤东地区70个雨量站点1980—2019年降雨资料为基础，采用反距离权重法(IDW)、径向基函数插值法(RBF)、普通克里金插值法(OK)、回归克里金法(RK)，分别对粤东地区降雨量进行空间插值计算，采用站点验证法进行插值结果评估，寻求最适合该区域的降雨空间插值方法，为进一步研究粤东地区水文模型、水生态环境、水资源管理等工作奠定数据基础。

1 研究区域概况及数据来源

1.1 区域概况

粤东地区地处广东省东南部，南临南海，北靠莲花山脉，地势北高南低，西北部和东北部主要是山地丘陵地带，平原主要分布在南部和东南部沿海地带，包括汕头、潮州、揭阳、汕尾4个地级市，总面积为 15 516万km2。属东南亚季风区，雨热同季，是全国光、热和水资源较丰富的地区，降雨主要集中在4—9月。受海洋性东南季风影响，雨量充沛，其中海丰、陆丰、揭西等雨量高区是省暴雨高区之一。粤东沿海也是西太平洋和南海热带气旋和台风经常登陆及影响的地区，风暴潮灾害时有发生。

1.2 数据来源

数据为粤东地区70个省水文局参编雨量站点40 a(1980—2019年)的逐月降水资料和坐标数据，时间序列连续，满足可靠性；样本容量大于30 a，满足代表性；对逐月降水资料进行统计处理，计算各站点年平均降水量和月平均降水量，并验证其正确性。

数字高程模型(DEM)为ASTER GDEM，是由NASA和MFTI于2009年6月共同发布的最新的全球高程数据。覆盖了99%的地球陆地面积，是迄今最完整的DEM数据。该DEM数据水平分辨率为30 m，垂直精度为±20 m，置信度均为95%[12]。利用ARCGIS软件进行数据拼接和掩膜裁剪得到粤东地区数字高程模型(见图1)。

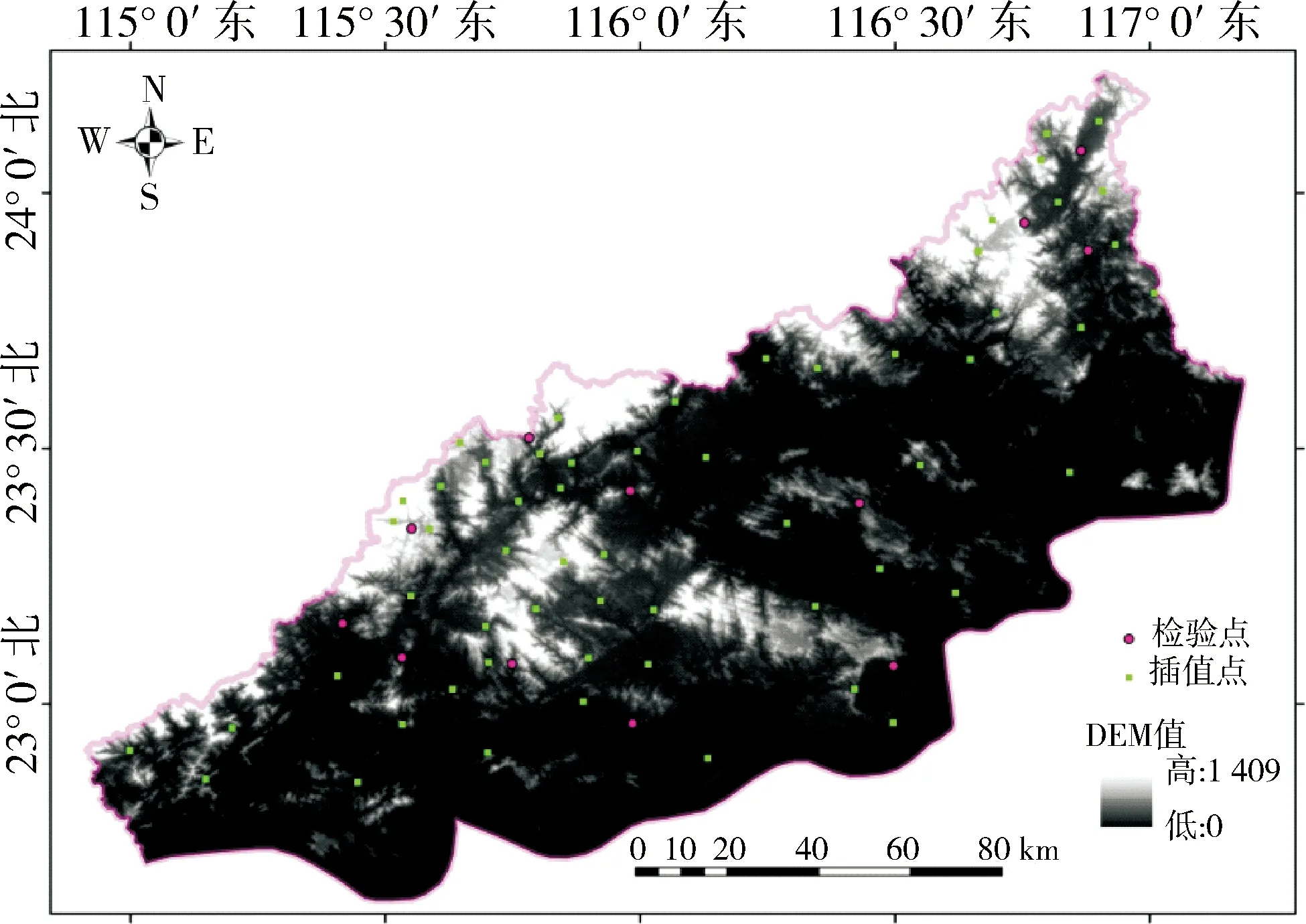
图1 粤东地区雨量站点分布示意

1.3 软件平台

本文中站点海拔高度、坡度、坡向等地形因子的提取、计算及降水量的空间插值和制图都在GIS软件ArcMap10.5下进行；多元线性回归分析采用SPSS软件。

2 研究方法

2.1 检验方法

采用站点检验法分别对4种方法在粤东沿海地区的插值结果进行评估。选取58个站点作为样本点用于降水插值计算，另12个站点数据作为实测值对空间插值得出的预测值进行误差分析。采用平均绝对误差(MAE)、均方根误差(RMSE)、皮尔逊相关系数(PPMCC)3种指标进行评估[13]。

(1)

(2)

(3)

式中：

Rei、Roi——第i个站点的预测值和实际观测值；

σe、σo——降雨量预测值和观测值的标准差。

2.2 多元线性回归分析

影响降水的因素很多，如地理位置、大气、地形、洋流、植被及水文状况、人类活动等。多元线性回归常用于一种现象与多种因素相联系，由多个自变量的最优组合共同来估计因变量，比只用某一个自变量进行估计更有效，更符合实际，用这种方法估算降水量不依赖于周围站点的密度，在各因子相关较强的情况下可以得到精度较高的模拟结果[14]。

本文将58个样本点的月平均降雨量、年平均降雨量分别与站点的经度、纬度以及通过DEM提取或得的坡度、坡向、海拔高度进行线性回归分析。表1中列出了粤东地区平均年降水量和平均月降水量分别与各地形因子的多元线性回归方程的回归系数。可以看出，平均降水量与经度显著负相关，尤其是年平均降水量和3—10月的月平均降水量，系数范围为-479.121～-15.724，表明平均降水量随着经度的增加而减少，递减率为479.1 mm/10E；月平均降水量在1—4月、7—10月和年平均降水量与纬度表现为正相关，系数范围为4.825～130.854，表明平均降水量大部分时候是随着纬度增加而增大；平均降水量与海拔高度全年表现为正相关，其中在1月、2月、7—12月以及年平均降水量表现为显著正相关，系数为0.013～0.523，表明降水量随海拔升高而变大；而平均降水量与坡度、坡向相关性都较差。综合得出，平均降雨与某一地形因子相关性并不是很稳定，随季节的变化存在差异性，而平均雨量与多地形因子构成的复相关系数全年除11月之外都为显著相关，复相关系数为0.327～0.763，明显优于某一地形因子相关性。

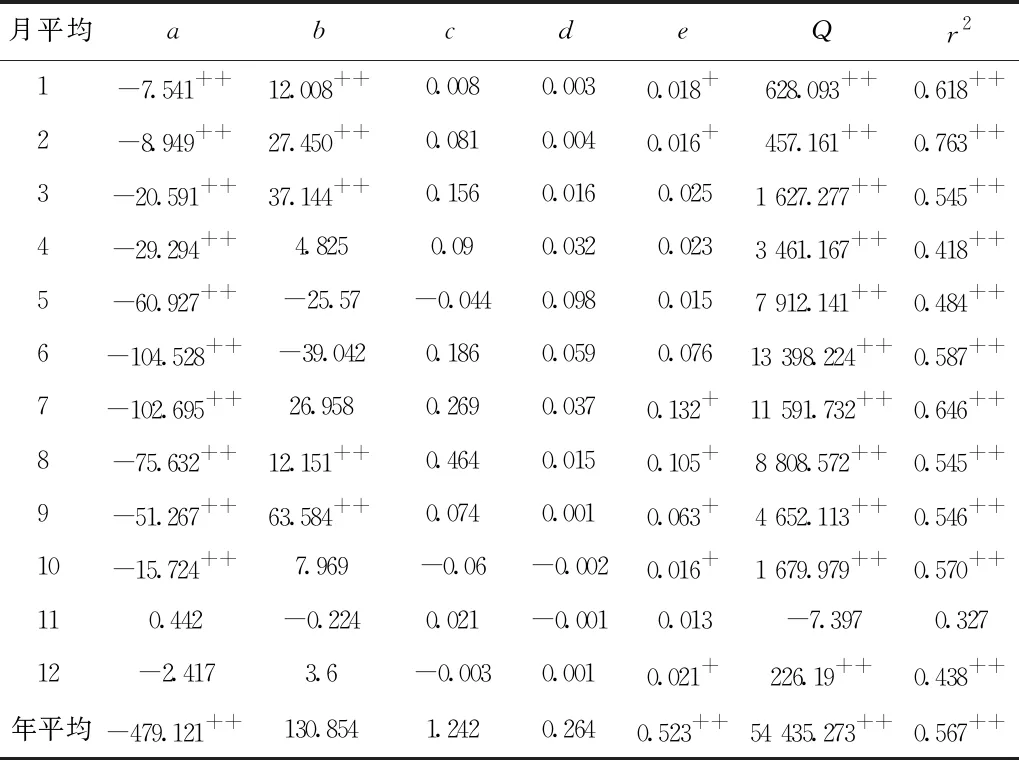
表1 粤东地区平均降水量与各地形因子的多元线性回归方程的回归系数

经上述分析，平均降水量及其变化情况需要通过经度、纬度、坡度、坡向海拔高度这些地形要素有效组合才可以反应出来，因此平均降水量的多元线性回归方程可表示为：

R=aE+bN+cS+dA+eH+Q

(4)

式中：

R——降水量；

E、N、S、A和H——分别是经度、纬度、坡度、坡向和海拔高度；

a、b、c、d、e——回归系数；

Q——常数项。

表2为粤东地区月、年平均降水量多元线性回归模型。

表2 粤东地区各月及年平均降水量多元线性回归模型

2.3 插值计算方法

2.3.1反距离权重法(IDW)

反距离权重法以待插值点到样本点间的距离为权重进行加权平均，认为与插值点距离越接近的若干样本点的权重越大，其贡献与距离成反比[6]。缺点是其计算值易受数据点集的影响，从而使计算结果常出现孤立点数据明显高于周围数据点的情况[7]。

2.3.2径向基函数插值法(RBF)

径向基函数插值法一种精确插值器，可以根据大量数据点生成平滑表面，可预测大于最大测量值和小于最小测量值的值。有薄板样条函数、张力样条函数、规则样条函数、高次曲面函数、反高次曲面函数五种基函数，这些函数可为平缓变化的表面生成很好的结果。缺点是表面值在短距离内出现剧烈变化和怀疑样本值很可能有测量误差或不确定性时这种插值方法不适用。

2.3.3普通克里金插值法(OK)

普通克里金是最早被提出和系统研究的克里金法，并随着地统计学的发展衍生出一系列变体和改进算法[8]。通过利用区域化变量的原始数据和变异数据的结构特点对未采样点的取值进行线性无偏最优估计[5]。

2.3.4回归克里金插值法(RK)

回归克里金是线性回归模型和克里金法相结合的算法，也是最常见的混合算法[9]。回归克里金首先使用建立辅助变量与目标变量之间的回归方程，然后利用回归方程对目标变量进行预测，并计算目标变量的残差，对残差进行克里金插值后，将残差的插值数据加到目标变量的回归值中从而得到一个新的预测值[5]。

3 结果与分析

3.1 年平均降水插值结果及分析

本文中IDW插值幂指数为2，站点最大搜索范围为临近15站，最小范围为临近10站；RBF插值中，利用GIS地统计工具依次对5种径向基函数进行插值预测，经交叉验证误差比较得出采用薄板样条函数进行插值效果最佳；对于OK插值，在考虑方向性的前提下依次利用GIS地统计工具对3种理论半方差模型进行了对比分析，得出在不考虑向异性的前提下用球面函数插值效果最佳；RK插值法由趋势项和残差项构成，趋势项为以降雨量为因变量，经度、海拔高度为自变量，建立的线性模型，残差项为对残差建立的克里金模型。4种插值结果见表3，站点检验法的各项误差及相关系数见表4。

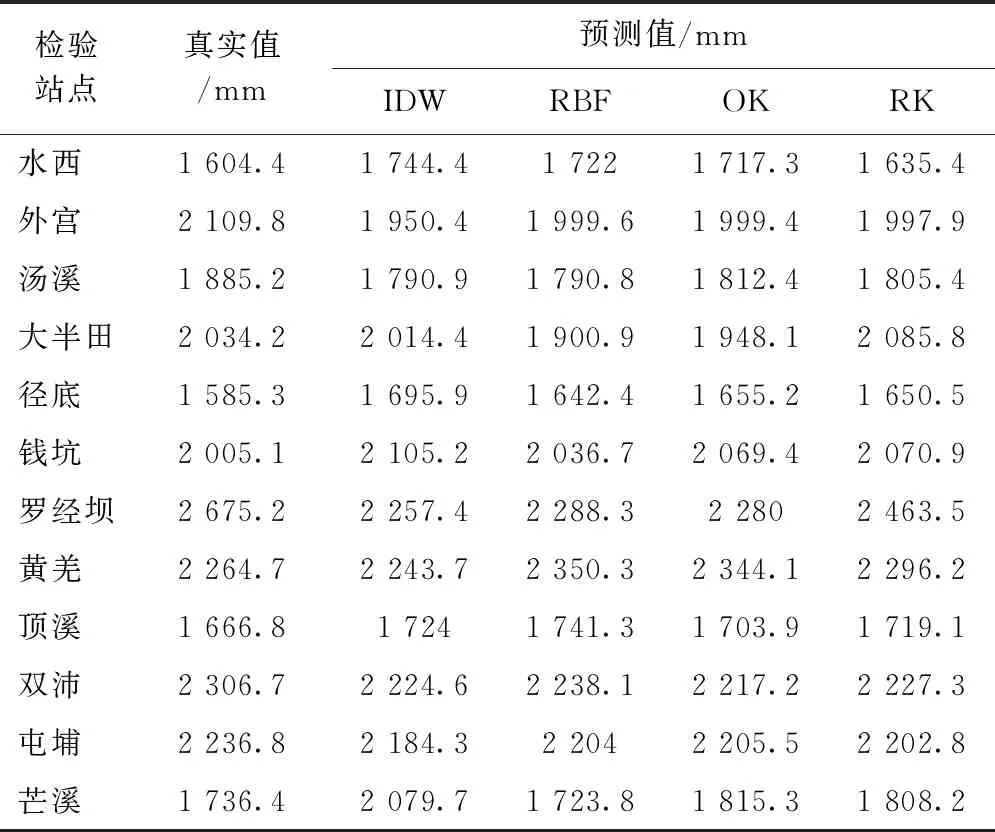
表3 12个检验站点年平均降水量不同插值方法结果

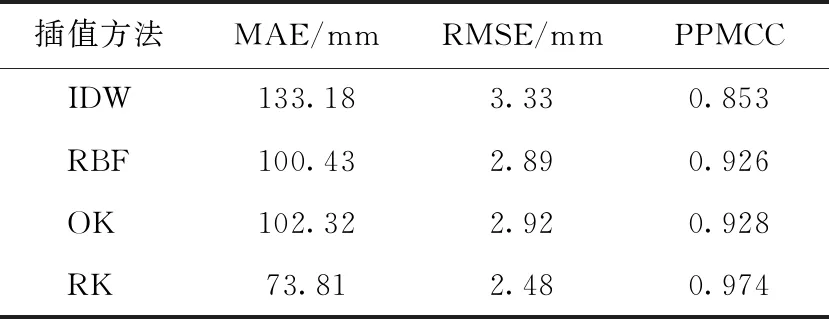
表4 4种插值方法的检验误差及相关系数

综上，考虑MAE和RMSE时，优劣顺序均为RK>RBF>OK>IDM，4种插值方法的预测值与实测值的相关系数都表现为显著相关。在年平均降水插值中，考虑了经度、纬度、高程、坡度和坡向的回归克里金法(RK)插值精度最好，其次是RBF法，再者是OK法，最差的为IDW法，分析原因为粤东地区为平原和山区混合地形，经纬度、海拔高度等地形因子对降水影响明显，RK法比较全面的考虑了这些影响因子，又通过较好的半方差模型的普通克里金插值法来修正残差，因此得到较好的插值效果(4种插值方法分别生成的粤东区域年平均降水量空间分布示意见图2)。

由图2可以看出，粤东地区雨量北多南少，西北部和东北部主要山地丘陵地带降雨量丰富，成为粤东地区降雨最多的地方，南部和东南部沿海地带的平原地带雨量最少。RK插值法受回归变量影响明显，呈现出与经度显著负相关，与海拔高度正相关，导致模拟的降水量存在空间变异比较大，有大数值雨量区分布在海拔较高地带(图2 a中的红色部分)，但也在一定程度上说明高海拔区域的小范围气候特征，且最大值大于其他3种插值方法模拟的降水量最大值500 mm左右，可以得出线性模型会造成模拟数据出现不太符合实际的极值情况，但现有站点并不能有效验证这种情况[5]。OK插值和RBF插值法模拟结果图表现为降水的空间连续性很强，总体趋势平滑且相近，插值结果基本一致。IDW插值法模拟结果图都有明显的极小值点，有圆形区域和条带区域[5]，即有明显的“锯齿”和“牛眼”现象[10]。

a 回归克里金插值法

3.2 月平均降水插值结果及分析

为了研究不同的插值方法在丰水期和枯水期时的插值效果，使用年平均降水相同的插值方法及参数，分别对58个样本站点月平均降水进行插值计算，采用MAE、RMSE、PPMCC3种指标对12个检验站点实测值和预测值进行评估，结果见图3。

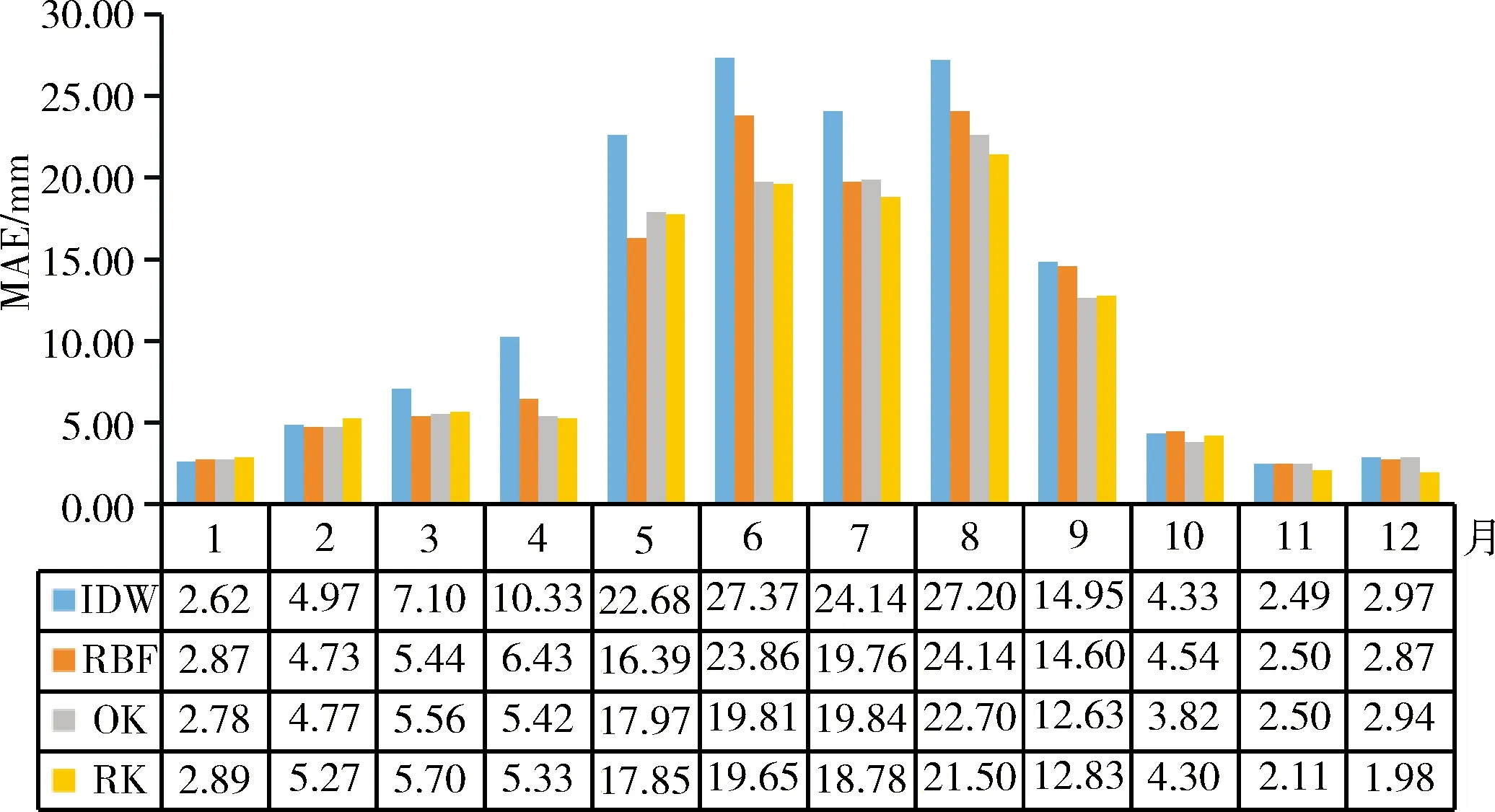
a MAE

由图3可得，RK插值方法整体精度最高，MAE为1.98～21.50 mm，均值为9.85 mm，RMSE为2.57～28.23 mm，均值为13.46 mm，PPMCC为0.797～0.951，全年表现显著相关；其次为OK插值方法，MAE为2.78～22.70 mm，均值为10.06，RMSE为3.63～29.90 mm，均值为13.84 mm；再者为RBF插值方法，MAE为2.50～24.13 mm，均值为10.68，RMSE为3.28～31.13 mm，均值为14.18 mm；IDW插值方法精度最差，MAE为2.49～27.37 mm，均值为12.60 mm，RMSE为3.42～34.40 mm，均值为16.07 mm。在丰水期(7—9月，月降雨量大于200 mm)，RK插值方法精度高的效果明显好于IDW、RBF法，和OK法，5月、6月，OK法略优于RK法；在枯水期，1月、12月(月平均降雨量小于40 mm)，IDW插值法效果最好，略优于RK法，指标PPMCC值更是在1月为0.965，为所有月份中拟合程度最好的；而在2月、3月，RBF插值法效果最佳。从图3中还可以看出，无论采用何种插值方法，不同月份插值精度相差较大，例如反映预测值和实测值的拟合程度的指标PPMCC在1月份为0.924～0.965，而在10月份为0.732～0.797，这说明插值精度不仅仅取决于插值方法还与数据本身的自相关性等有关系。

4 结语

以70个雨量站点40 a降水资料为基础，采用IDW插值法、RBF插值法、OK插值法、RK插值法，对粤东地区年平均降水量和月平均降水量分别进行空间插值，采用站点验证法对插值结果进行评估研究，主要结论有：

1) 将月平均降雨量、年平均降雨量分别与站点的经度、纬度以及通过DEM提取或得的坡度、坡向、海拔高度进行线性回归分析。得到平均降水量与经度显著负相关，在丰水期表现尤为明显；与纬度在1—4月、7—10月和年平均降水量表现为正相关；与海拔高度全年表现为正相关，其中在1月、2月、7—12月以及年平均降水量表现为显著正相关；与坡度、坡向相关性都较差。综合分析得出，粤东地区平均降雨与某一地形因子相关性并不是很稳定，随季节的变化存在差异性，需要通过经度、纬度、海拔高度这些地形要素有效组合才可以反映出来。

2) 在年平均降水插值中考虑了经度、纬度、海拔高度的RK插值法精度最好，其次是RBF法，再者是OK法，最差的为IDW法，分析原因为粤东地区为平原和山区混合地形，经纬度、海拔高度等地形因子对降水影响明显，RK插值法比较全面的考虑了这些影响因子，又通过较好的半方差模型的OK插值法来修正残差，因此得到较好的插值效果。

3) 在丰水期，RK插值法和OK插值法精度明显好于RBF和IDW插值法。在枯水期，四种插值方法精度都比较高，RBF插值法和IDW插值法效果略好。