二维不可压Navier-Stokes-Landau-Lifshitz-Bloch方程的整体弱解的存在性
2022-04-22申会玲
申会玲
(广州大学 数学与信息科学学院, 广东 广州 510006)
0 引 言
本文研究不可压Navier-Stokes-Landau-Lifshitz-Bloch方程:
∂tρ+div(ρu)=0
(1)
∂t(ρu)+div(ρu⊗u)+∇p=μΔu-λ∇·(∇d⊙∇d)
(2)
∂td+u·∇d+α1d×Δd=α2Δd-α3(1+|d|2)d
(3)
divu=0
(4)
其中,(x,t)∈Ω×(0,T),Ω={x=(x1,x2)||xi|
其初始条件:
(ρ,u,d)|t=0=(ρ0,u0,d0)
(5)
在式(1)~(4)中,若d是常向量,则原方程是一个常粘性非齐次不可压Navier-Stokes方程。现在对于一般的Navier-Stokes方程组的研究相对成熟,Lions[1]对不可压Navier-Stokes方程组作了比较系统性的研究,对可压缩的Navier-Stokes方程组的研究主要见Lions[2]和Feireisl等[3- 4]。但是对于三维Navier-Stokes方程组的弱解的正则性和唯一性问题至今仍未解决。
若取式(1)~(4)中u=0,ρ是一个常数,并且如果式(3)中α2Δd-α3(1+|d|2)d项是d×(d×Δd),则式(1)~(4)变为Landau-Lifshitz方程[5-6]
∂td=d×Δd-λd×(d×Δd)
(6)
式(6)无耗散项时为
∂td=d×Δd
(7)
对于式(7),Alouges等[7]和Sulem等[8]讨论了在一定条件下该方程的弱解的存在性及唯一性问题;郭柏灵等[6]、Zhou等[9-11]和You等[12]证明了在一维情况下的整体弱解的存在性、非线性初边值问题整体弱解的存在性,及多维情况下整体弱解的存在性。对于式(6)的解的存在性问题,Guo等[13]在1997年已经讨论,在文中证明了式(6)局部弱解的存在性,又通过拓展得到整体解的存在性。
当不考虑速度和密度时,式(1)~(4)就是Landau-Lifshitz-Bloch方程[14-15]
∂td=Δd+d×Δd-λ|d|2d,
对此方程的研究近年有显著进展:2016年Le[16]证明了方程弱解的存在性,并讨论了弱解的正则性;2019年Ayouch等[17]讨论了一类含Caputo分数阶弱导数的时空Landau-Lifshitz-Bloch方程弱解的整体存在性并推导出在一维空间情况下的唯一性;近两年Jia和Guo等[18-20]研究了m维闭黎曼流形上的Landau-Lifshitz-Bloch方程局部解的存在性、一维可压缩Landau-Lifshitz-Bloch方程初值问题的整体光滑解的存在唯一性、具有周期初始值的Landau-Lifshitz-Bloch方程在二维和三维空间中其光滑解的存在唯一性。
本文参考Wang等[21]证明二维Navier-Stokes-Landau-Lifshitz方程弱解的存在性的Feado-Galerkin方法,研究二维不可压Navier-Stokes-Landau-Lifshitz-Bloch方程的整体弱解的存在性。
下面给出本文的主要结果:
定理1(存在性) 假设初始数据满足以下条件:
(8)
u0∈L2(Ω), ∇d0∈L2(Ω),divu0=0
(9)
则对任意的T>0,式(1)~(4)存在弱解(ρ,u,d)且满足:
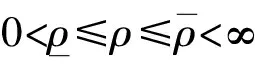
(10)
u∈L∞([0,T];L2(Ω))∩L2([0,T];H1(Ω))
(11)
d∈L∞([0,T];H1(Ω))∩L2([0,T];H2(Ω))
(12)
1 预备知识
在这里先给出一些符号表示。在本文中C是变常数;Wk,p和Hs是Sobolev空间,Lp([0,T];Lq(Ω))是带有时间的Sobolev空间,其中的元素关于时间变量p次可积,关于空间变量q次可积。
引理1(Gagliardo-Nirenberg不等式)[22]假设Ω⊂Rd(d≥1)是一个有界开集,且满足∂Ω∈C0,1,m∈N,1≤p,q,r≤∞,那么存在常数C>0使得∀u∈Wm,p(Ω)∩Lq(Ω)有
其中,0≤|α|≤m-1,θ=|α|/m且|α|-d/r=θ(m-d/p)-(1-θ)d/q;若m=|α|-d/p∉N0,θ∈[|α|/m,1]上述不等式也成立。
引理2(Sobolev嵌入定理)[23]Sobolev空间Wk,p(Rn),若k>l且1≤p Wk,p(Rn)⊆Wl,q(Rn) 并且此嵌入连续。在k=1且l=0的特殊情况下有 W1,p(Rn)⊆Lp*(Rn), 其中,p与p*是Sobolev共轭:1/p*=1/p-1/n. 特别地,由引理1与引理2有下列不等式在n=2的情况下成立,且将在下节中用到: 若u∈L2(Ω)且∇u∈L2(Ω),则有 (13) 引理3(Aubin-Lions引理)[24]假设Banach空间X,Y,Z满足X⊂Y⊂Z并且X→→Y,则有 Lq([0,T];X)∩{φ:∂tφ∈L1([0,T];Z)}→→Lq([0,T];Y),∀1≤q≤∞, L∞([0,T];X)∩{φ:∂tφ∈Lr([0,T];Z)}→→C([0,T];Y),∀1≤r≤∞。 在本节中通过构造逼近解,说明了其局部存在性,又对逼近解做一致整体的线性估计,从而证明弱解的整体存在性。 首先构造一个逼近解序列: 令 V={h∈L2} (14) -Δw=λjw, -Δη=δjη, 对于∀m,n,式(1)~(4)有近似解umn和dmn: (15) (16) 那么就有 ∂tρmn+umn·∇ρmn=0 (17) (18) (19) ρmn(x,0)=ρ0mn(x),umn(x,0)=u0mn(x), dmn(x,0)=d0mn(x) (20) 其中,j=1,2,…m。式(17)~(20)是关于gjmn和hjmn的常微分系统,根据常微分方程组存在性理论可以得到∃T0>0,使得常微分系统式(17)~(20)有光滑解(gjmn,hjmn),并且可以将解延拓到区间[0,T]。 下面对上述的逼近解进行先验估计。 引理4假设定理1的条件成立,则式(17)~(20)的解满足如下估计: (21) (22) 证明根据式(17)由特征线法易证得式(21),现证式(22)。 在式(18)中选取umn为测试函数 (23) 在此用到由式(17)得到的一个事实 (ρmnumn·∇umn)·umndx。 类似地,式(19)中选取Δdmn为测试函数 α3|dmn|2|∇dmn|2+ (24) 同时又注意到,通过分部积分有 式(23)~(24)的λ倍相加得 (25) 根据引理4,用Gronwall不等式易得下列推论。 推论1下列不等式成立 ‖umn‖L∞([0,T];L2(Ω))+‖umn‖L2([0,T];H1(Ω))≤C (26) ‖dmn‖L∞([0,T];H1(Ω))+‖dmn‖L2([0,T];H2(Ω))≤C (27) 引理5下列估计成立 ‖∂tumn‖L2 ([0,T];H-1(Ω))≤C (28) 证明由式(18)、式(13)和分部积分可得 |μ|‖∇umn‖L2([0,T];L2(Ω))‖∇φj‖L2([0,T];L2(Ω))+ c‖umn‖L∞([0,T];L2(Ω))‖∇umn‖L2([0,T];L2(Ω)) ‖∇φj‖L2([0,T];L2(Ω))+c‖∇dmn‖L∞([0,T];L2(Ω)) ‖Δdmn‖L2([0,T];L2(Ω))‖∇φj‖L2([0,T];L2(Ω)), 即‖∂tumn‖L2([0,T];H-1(Ω))≤C得证。 引理6 ‖∂tdmn‖L2([0,T];H-1(Ω))≤C (29) 证明由式(19)知 通过分部积分可得 因此, ‖umn‖L∞([0,T];L2(Ω))‖dmn‖L2([0,T];L∞(Ω)) ‖∇ψj‖L2([0,T];L2(Ω))+ |α1|‖dmn‖L2([0,T];L∞(Ω))‖∇dmn‖L∞([0,T];L2(Ω)) ‖∇ψj‖L2([0,T];L2(Ω))+|α2|‖∇dmn‖L2([0,T];L2(Ω)) ‖∇ψj‖L2([0,T];L2(Ω))+ |α3|‖dmn‖L2([0,T];L2(Ω))‖ψj‖L2([0,T];L2(Ω))+ ‖ψj‖L2([0,T];L2(Ω))。 由Sobolev嵌入易得 ‖∂tdmn‖L2([0,T];H-1(Ω))≤C。 上述所有估计的界与m和n无关,根据Sobolev嵌入定理和Aubin-Lions引理知可选择 (ρmn,umn,dmn)的子序列(仍记为(ρmn,umn,dmn)),使得当m→∞或n→∞时 umn⇀u,弱收敛,在L2([0,T];H1(Ω))中 (30) umn⇀u,弱*收敛,在L∞([0,T];L2(Ω))中 (31) umn→u,强收敛,在L2([0,T];L2(Ω))中 (32) umn→u,几乎处处收敛,在L2([0,T];L2(Ω))中 (33) 类似可得 dmn→d,弱收敛,在L2([0,T];H2(Ω))中 (34) dmn→d,弱*收敛,在L∞([0,T];H1(Ω))中 (35) dmn→d,强收敛,在L2([0,T];H1(Ω))中 (36) dmn→d,几乎处处收敛,在L2([0,T];H1(Ω))中 (37) 由上述收敛,易得下列收敛 (38) (39) (40) (41) (42) 接下来考虑其余非线性项: 因为在L2([0,T];L2(Ω))中,umn→u,强收敛且几乎处处收敛,且在L2([0,T];H1(Ω))中,umn⇀u,据弱收敛引理有下列收敛 (43) 类似地有 (44) u·∇d)·ψjdxdt= 在m→∞或n→∞时,|I1|→0,|I2|→0,即 (45) 类似可得 (46) ψjdxdt (47) 因为φj和ψj是单位正交基,所以对∀φ∈H,ψ∈V,φ(·,T)=ψ(·,T)=0,下式成立 (48) (49) 至此,方程(1)~(4)的弱解的整体存在性证明完毕。 本文首先通过经典的Faedo-Galerkin方法构造出了方程的近似解,接着对近似解进行先验估计,得到与近似解相关的一致有界估计,最后由紧性理论有相应的收敛性,从而证明整体弱解的存在性。 本文只是该方程的解的适定性的初步研究,仅证明了该方程在二维空间上弱解的存在性,对于弱解的唯一性及正则性等适定性问题还没有做出相应的研究,而且关于更高维空间里的相应问题也是值得研究的。后续研究将继续致力于解决上述问题。 致谢感谢广州大学数学与信息科学学院教师王光武、蒲学科对本论文的悉心指导。
2 存在性证明

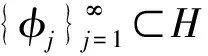
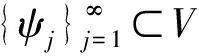

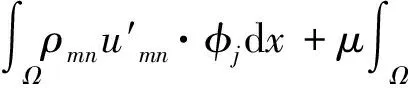

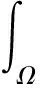
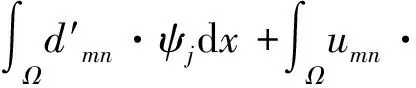





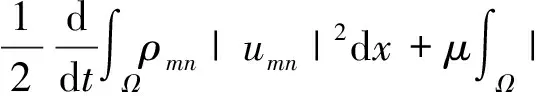

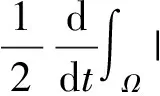
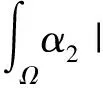


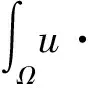
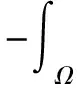




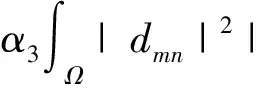
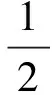

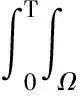
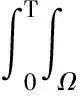

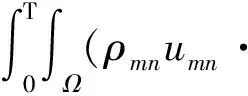












3 总结与展望
