期刊引文评价新指标JCI 特点研究

宗张建

(南京医科大学 图书馆,江苏 南京 211166)

0 引言

引文是表征期刊学术影响力的重要方式。 1955年,E.Garfield 首次基于“引用关系”提出影响因子的概念;1963 年,E.Garfield 与H.Irving 创立期刊影响因子(JIF);1976 年,E.Garfield 创办的科学信息研究所出版了第一期期刊引证报告(JCR),报告提供了详细的期刊引用数据,并发布了完整的影响因子列表[1]。 至此,这种利用引文分析评估期刊影响力的方法得到了期刊出版乃至科研人员的广泛关注,影响因子也成为影响最大、使用最广泛的期刊影响力计量指标。 然而,影响因子也存在诸多局限,如不能排除自引操纵、评价周期过短、引文同质对待、不能跨学科比较等。 因此,近年来JCR 相继推出他引影响因子(JIF Without Self Cites)、五年影响因子(5 Year JIF)、特征因子(Eigenfactor)、论文影响力(Article Influence Score)、影响因子百分位(JIF Percentile)等计量指标,用以补充和丰富期刊评价指标库。 2021 年,JCR 再增加了一个新指标——Journal Citation Indicator(JCI)。科睿唯安公告宣称,该指标通过对不同科研领域、文献类型以及引用比率进行标准化处理,以便于跨学科解释和比较[2]。

引文标准化(Standardization)处理是消除文献发表时间、类型以及学科差异的有效方法。 JCI 作为JCR 新提出指标,其计算原理、与影响因子的差异、指标数值分布特点、与其他期刊影响力指标相关度等均需进一步深入分析。 本文从JCI 计算原理入手,通过实证数据分析指标数值分布特征以及与影响因子的区别,并通过相关性检验,进一步分析JCI 与其他期刊计量指标的关系。

1 JCI 计算方法

学科规范化引文影响力指标(Category Normalized Citation Impact,CNCI)是JCI 的上游指标,该指标可实现论文级别的被引频次标准化[3]。 具体是,对于单篇论文i,当其仅归属于一个学科领域时,其CNCI值是通过其实际被引次数除以同文献类型、同出版年、同学科领域文献的期望被引次数获得的。 计算公式如下:

但当一篇论文i归属于n个学科领域时,则该篇论文的CNCI 值为每个学科领域实际被引频次与期望被引次数比值的平均值:

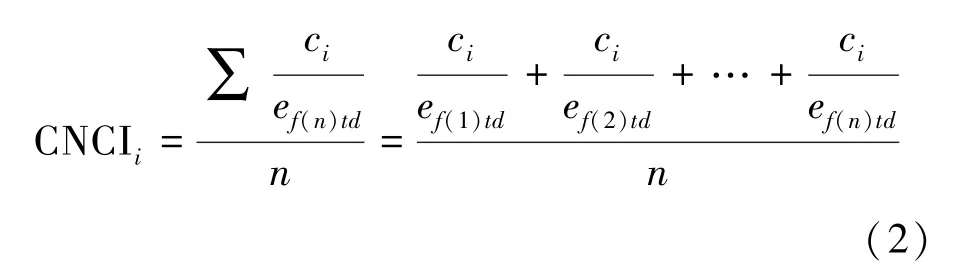
式中:ci为单篇论文被引频次;e表示同学科同出版年同文献类型的论文平均被引次数(基线);f,t,d分别表示学科领域、年份和文献类型;n为论文归属的学科数量。

CNCI 排除了出版年、学科领域与文献类型对被引频次的影响,是一个无偏影响力指标。 在实践中,通常还可以通过计算一组论文集CNCI 的平均数,实现不同分析对象(如国家、机构等)学术成果影响力的比较。 JCI 的定义就是期刊过去3 年发表的所有论文和综述的CNCI 平均值[2],计算方式如下。

式中,θ表示JCR 出版年。 CNCI 的基准值是1,当论文CNCI 值高于1 时,表明论文引用超过全球平均水平;当论文CNCI 值低于1 时,则表明论文引用低于全球平均水平。 同理,数值1 也是衡量期刊引用表现的基准值。 当JCI 值高于1 时,表明该期刊超过所有期刊的平均引用水平;当JCI 低于1 时,即表明该期刊引用表现未达到平均引用水平。

2 JCI 基本特点

2 1 研究数据

为了了解JCI 数值的基本特点,本文选择数学学科(Mathematics)期刊为研究对象。 在2020 年度JCR中,数学学科是期刊数量最多的学科,较大的样本量可保证研究的稳健性[4]。 但需注意的是,2020 年度JCR 较往期出现较大变化。 变化之一就是扩大了JCR 收录期刊的范围,不仅包含原有的SCI/SSCI 期刊,同时还将ESCI 等索引期刊纳入。 如2020 年度JCR 收录的471 本数学学科期刊中,SCIE 收录期刊有330 本,ESCI 期刊则有141 本。 但ESCI 期刊没有获得期刊影响因子以及相关衍生指标数据。 此外,部分SCIE 期刊也存在少数指标数据缺失的情况。 因此,为了保证分析数据的完整性,本次研究尽量纳入全部样本数据,并利用SPSS 18.0 对相关数据进行分析。各指标的描述统计如表1 所示。

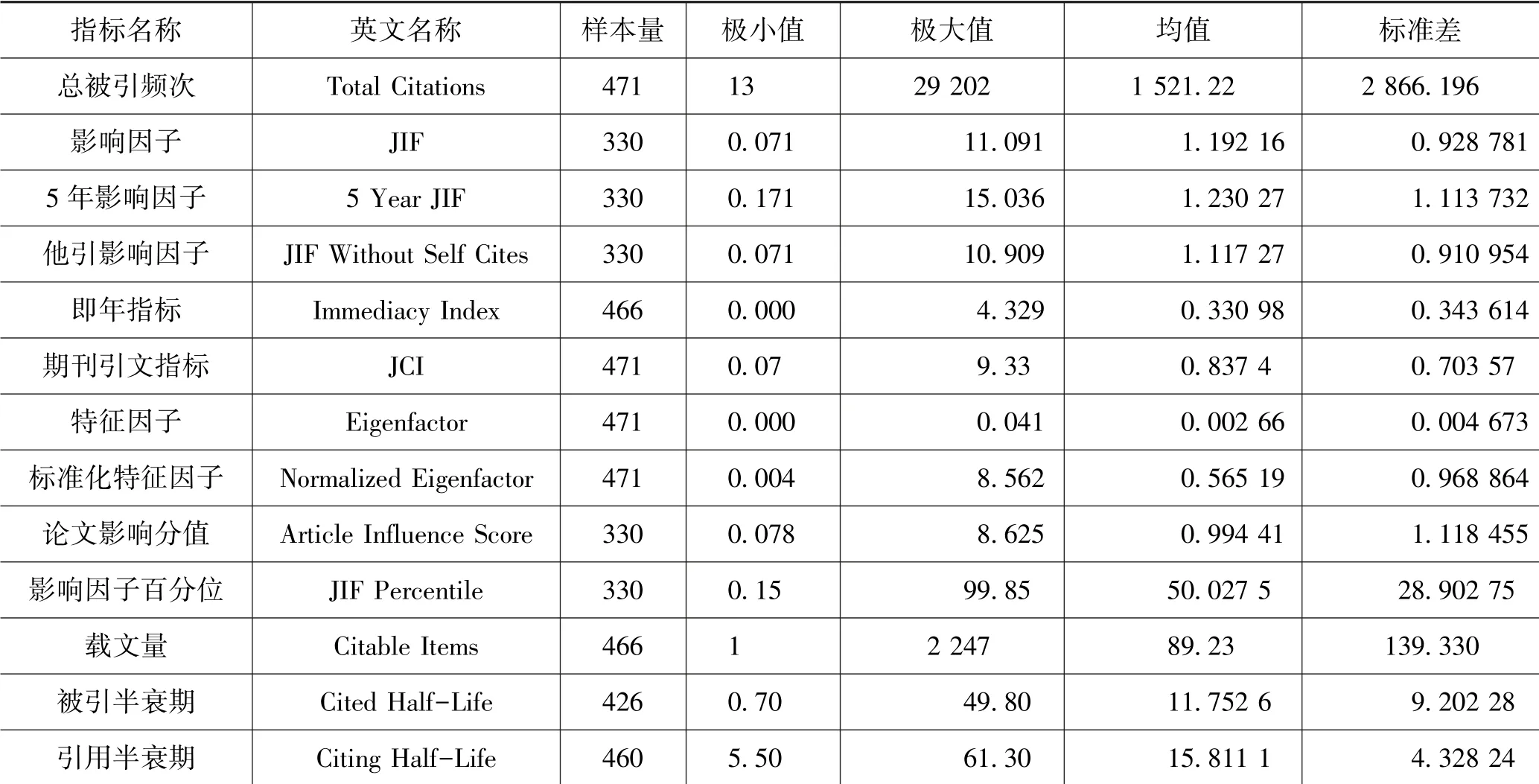
表1 指标描述统计

2.2 JCI 数值分布特征

对471 本样本期刊JCI 数据进行正态性检验,频数分布图(见图1)和正态Q-Q 图(见图2)均提示JCI数值不服从正态分布。 以基准值1 为分界值,471 本期刊中,JCI 低于基准值的期刊有350 本,占全部期刊的74.3%;JCI 等于或高于基准值1 的期刊有121 本,占全部期刊的25.7%。 即使在SCIE 期刊中,也有216 本期刊JCI 值低于1,占全部SCIE 期刊的65.5%。 因此,JCI 数值呈偏态分布,引用水平低于平均水平的期刊占多数。

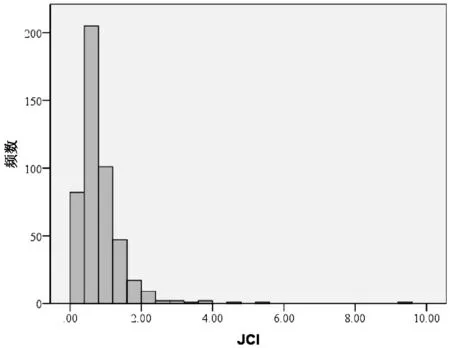
图1 JCI 频数分布图

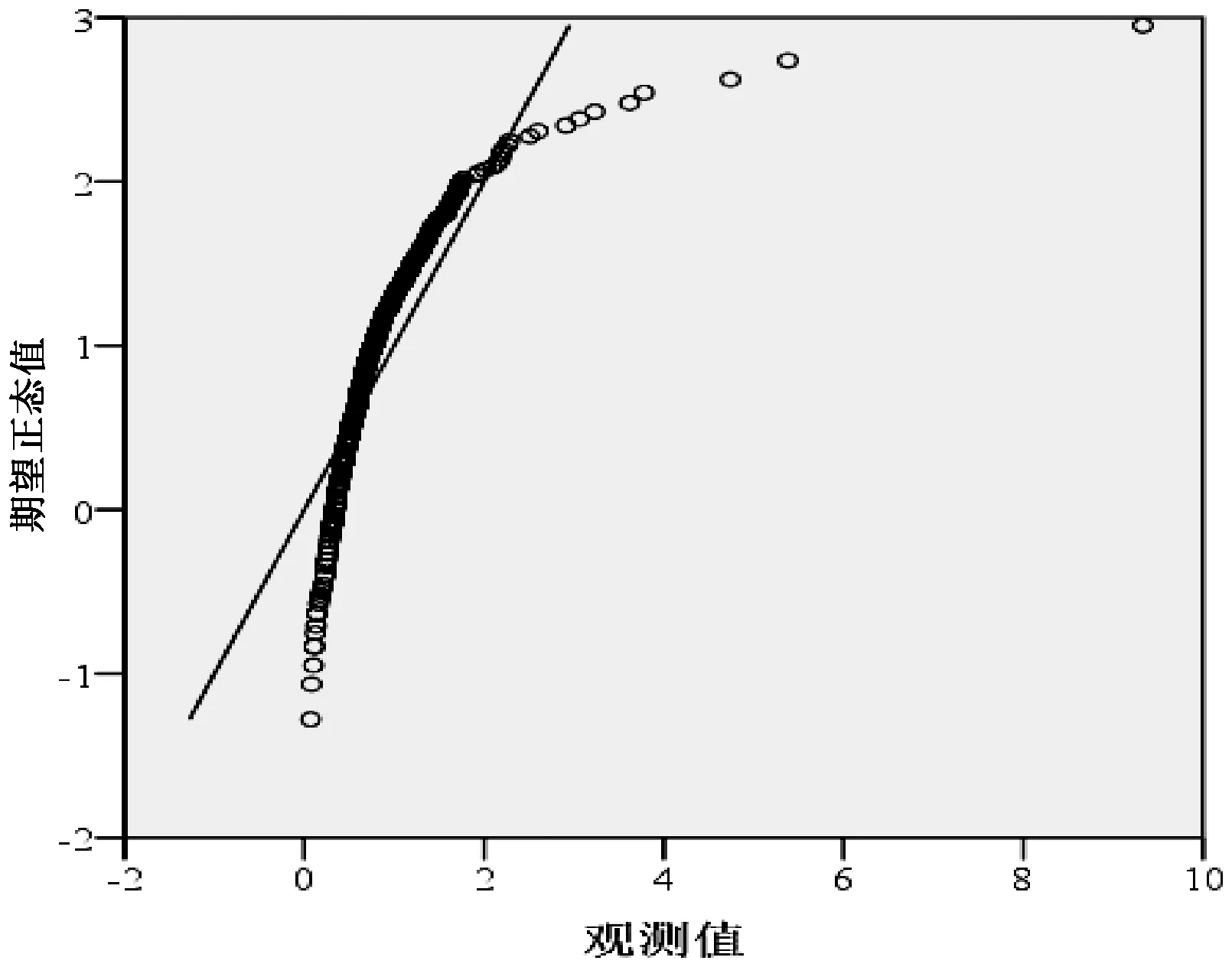
图2 JCI 的正态Q-Q 图

进一步比较JCI 与影响因子的统计学特征,以330 本同时包含两项指标数据的SCI 期刊为研究对象,对比分析两项指标极值、极差、均值、标准差、偏度和峰度的差异。 结果(见表2)显示,JCI 数值分布的极差、均值以及标准差均小于影响因子。 这表明,JCI的离散性较小,且JCI 的值比影响因子更为集中,JCI减弱了具有较高影响因子期刊的优势。 此外,JCI 数值的偏度和峰度稍高于影响因子,表明JCI 数据的不对称性和陡峭性高于影响因子。

表2 JCI 与影响因子的统计学特征分析

2.3 JCI 与期刊影响力指标的相关性

为了分析JCI 与其他文献计量指标的关系,本文采用斯皮尔曼(Spearman) 相关系数进行分析。Spearman 相关系数可用于非正态分布数值的相关性检验。 分析结果(见表3)显示,JCI 与影响因子、5 年影响因子、他引影响因子以及影响因子百分位高度正相关,相关系数在0.9 左右;与总被引频次、即年指标、特征因子、标准化特征因子、论文影响分值中度正相关;与载文量、引用半衰期相关度较低。 此外,被引半衰期的相关系数没有通过统计检验。

表3 相关系数

3 分析与讨论

3.1 JCI 的优缺点

相较于影响因子,JCI 的优点表现在两个方面。首先,JCI 延长了期刊引用区间。 影响因子计算的引用区间是2 年,而JCI 将引用区间延长为3 年,这在一定程度降低了不同主题领域引用行为的差异。 其次,JCI 采用了论文出版后所有的引用,并将其进行标准化处理,而影响因子只采用了论文在JCR 当年的引用,且未经过标准化处理。 经过标准化处理后的数据可以按照一个统一的标准进行比较,增强了数据的可比性。

但从指标特征本质上看,JCI 与影响因子一样,均属于平均数指标。 影响因子可认为是期刊论文平均被引频次;而JCI 则是期刊的标准化平均被引频次,其分母为期刊论文集合的论文数量,分子是标准化的论文总被引频次。 这一点或许解释了JCI为何与影响因子及其相关衍生指标高度正相关的原因。 因此,JCI 在指标设计上仍存在与影响因子类似的缺陷。 首先,JCI 作为平均数指标,容易受期刊高被引论文和零被引论文引用极值的影响。其次,JCI 没有对期刊的自引情况进行相应的处理,因此JCI 不能排除自引操纵。 最后,JCI 存在引文同质对待。 JCI 将每一条引文的作用都看成是相同的,没有区分不同引用的权重,因而没有体现高影响力引文在期刊评价中的重要性。

3.2 JCI 的挑战

尽管科睿唯安声称JCI 作为一个单一的期刊级别指标,为轻松地进行跨学科解释和比较提供了可能。 但TheScholarlyKitchen编辑P.Davis 依然从计算结果的科学性、透明度以及可重复性提出了质疑[5]。JCI 的第一个挑战是计算结果的科学性。 JCI 的计算严重依赖期刊学科划分体系,而Web of Science(WoS)的期刊分类多基于“刊与刊”的关系。 目前,WoS 数据库使用235 个学科类别,但随着科学的发展,期刊的主题可能随着时间而变化。 此外,大约三分之一的期刊被分配到多个主题类别中。 种类繁多的主题可能对JCI 的计算造成混乱。 JCI 的第二个挑战是数据透明度和可重复性。 JCI 依赖学科数据集的平均引用次数,但对于大多数用户而言,用于重新创建指标的整个数据集和方法基本上是不可行的。