深水钢桩起吊下放运动特征分析

黄山田，王浩宇，魏佳广，李晓琛，刘 松

海洋石油工程股份有限公司，天津 300461

随着我国海洋战略的快速推进，深水油气平台与海上风电场已成为一个重要的发展方向，桩基基础作为这两种能源平台的共有基础形式，其安装的精度对平台结构的在位性至关重要[1]。通过对钢桩起吊和入水安装过程中运动特点的模拟分析，研究影响钢桩运动和就位精度的关键因素，从而达到减小钢桩安装精度超差风险的目的，该技术对于制定钢桩稳定下放及精确就位施工方案至关重要，有助于解决平台安装技术中的关键环节，从而保障海洋油气平台和风电结构的在位性能，有效地提高安装效率，助力于“一带一路”海洋战略的实施。

1 基础参数

本文选取位于325 m水深的南海近海海域某大型导管架及其钢桩设计作为工程实例，对钢桩起吊和下放关键过程进行运动特点计算分析。钢桩的设计尺寸及质量分布见表1、图1。

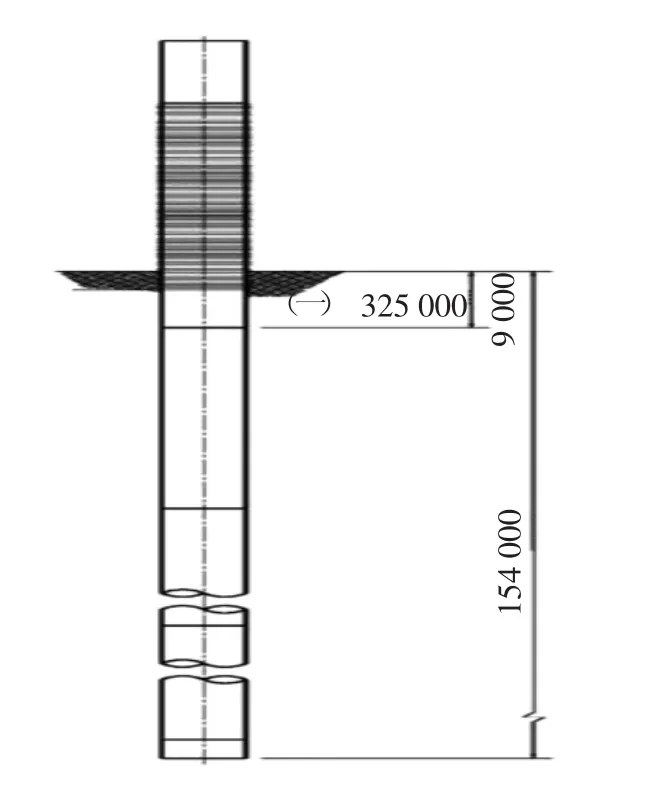
图1 钢桩的设计尺寸

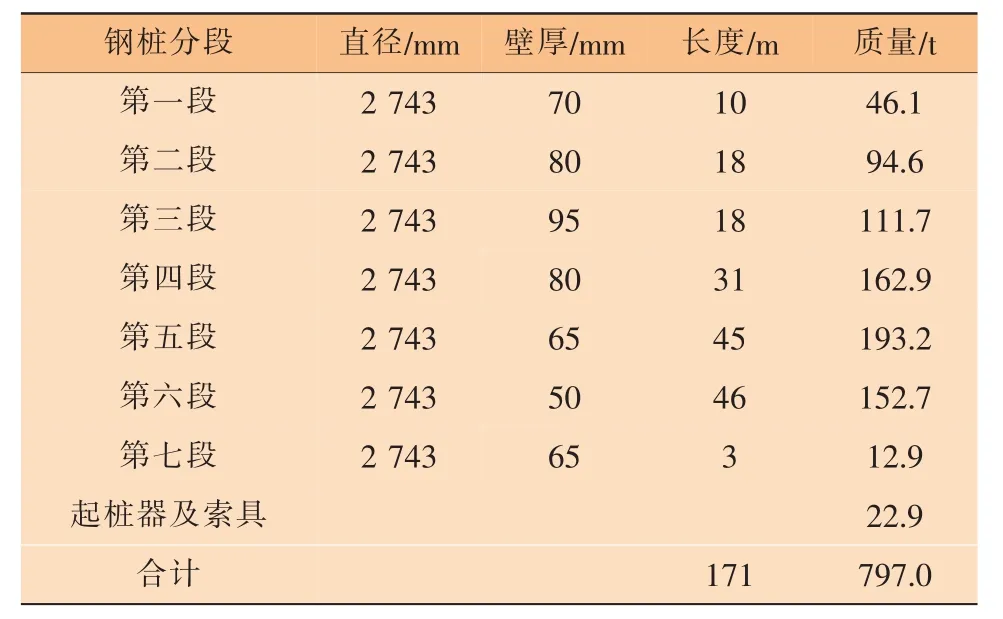
表1 钢桩的设计尺寸及质量

钢桩起吊及下放计划采用海油工程“蓝鲸”号大型起重工程船，见图2。作为国内单臂起重能力最大的安装船舶之一，“蓝鲸”号全长241 m，宽50 m，型深20.4 m，起重吊梁高98.1 m，最大起重能力75000kN。“蓝鲸”号吊钩可深入水下150m，最高起吊高度可达110 m。

图2 "蓝鲸"号大型起重船

基于“蓝鲸”号锚系船的钢桩可行性研究考虑了风、浪、流环境载荷下船体的平移、低频运动及线性高频运动。本文仅针对基于响应幅值算子（RAO）的线性运动部分做运动分析[2]。“蓝鲸”号的运动响应特征见图3。

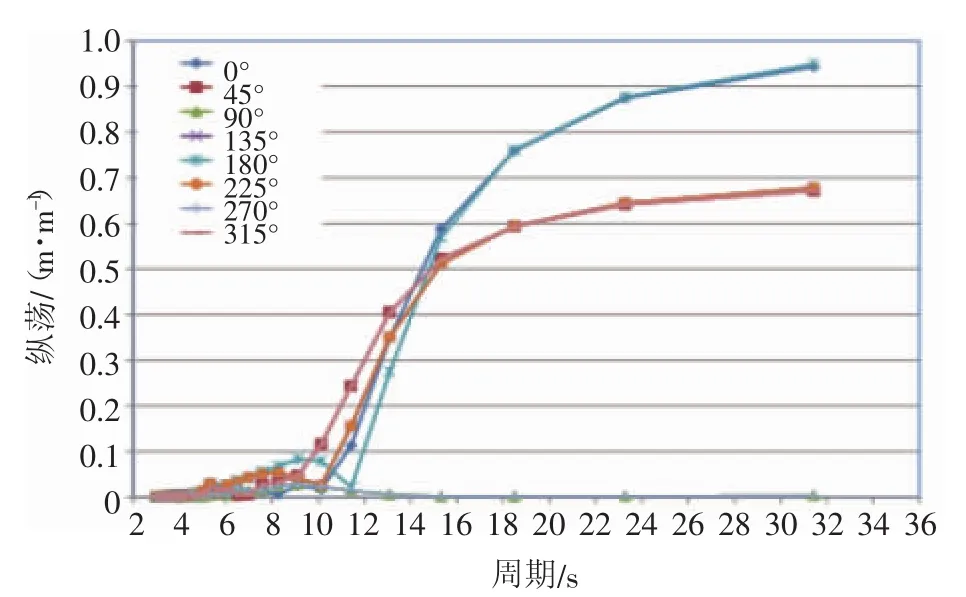
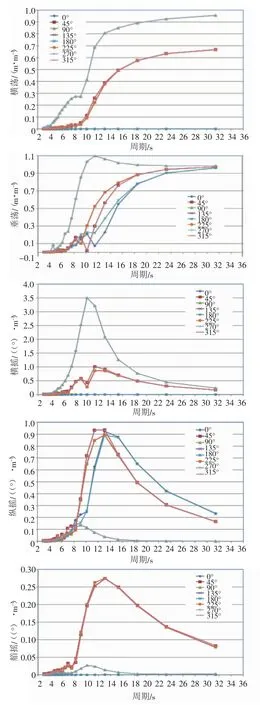
图3 "蓝鲸"号运动特征（RAO）

2 运动特征分析

采用Orcaflex10.2版软件对本工程实例中钢桩的吊装进行分析。Orcaflex由Orcina开发，广泛用于海洋工程系统安装和设计的静态与动态分析[3]。典型计算模型见图4。吊装钢缆采用两根ϕ60mm×11m钢丝，单位长度吊装钢丝总质量为316.2kg/m，钩头质量约为57 t。

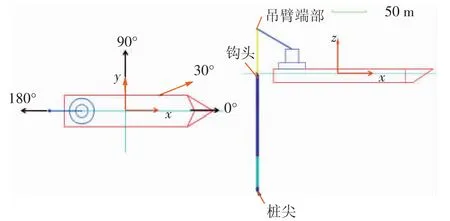
图4 运动特征分析计算模型及坐标系

动态计算分析考虑了下列吊装下放过程中几个代表性位置。

工况LC1：桩尖位于泥面以上150 m处（对应钩头在海平面附近，水下4 m）。

工况LC2：桩尖位于泥面以上60 m处（对应钩头在海平面附近，水下94 m）。

工况LC3：桩尖位于泥面以上30 m处（对应钩头在海平面附近，水下124 m）。

计算分析涵盖了对应限制有义波高Hs=2.0 m的当地海况波浪周期范围Tp=4.0～13 s，来浪方向考虑每30°间隔的不同方向来浪。来流对钢桩运动特点的影响也在本文范围内。

如图4所示，来浪及来流方向角度定义为相对于X方向（船头方向） 的夹角：0°为顺浪，180°为顶浪方向，和RAO的定义保持一致。海流速度沿水深分布见表2。

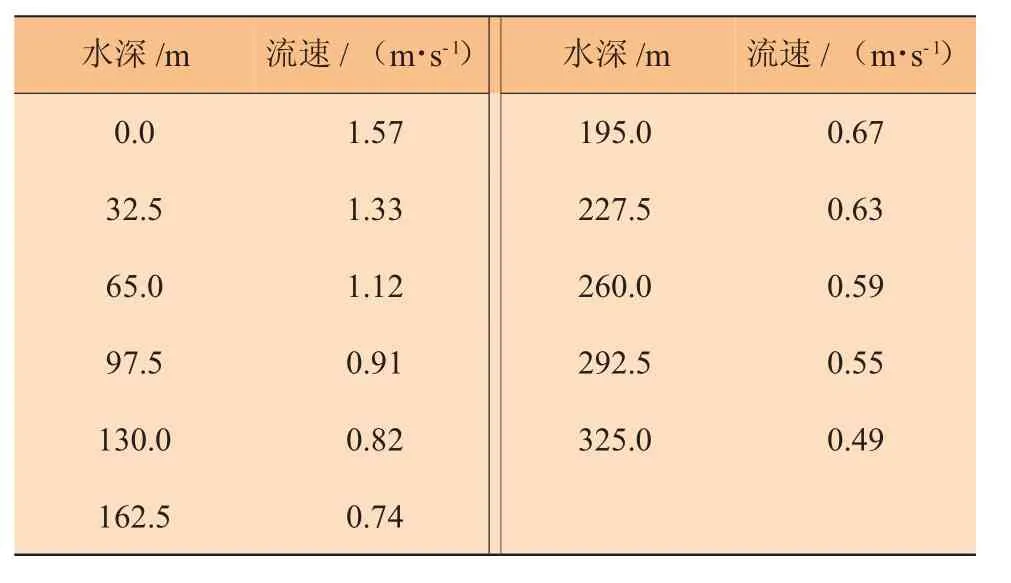
表2 流速沿水深分布：1年返回期最大流速

钢桩在水面以上扶正及通过水溅区的运动分析没有包含在本文内容中。

2.1 水平面内运动特征（横向运动X、Y）

计算分析截取了3个代表性位置来研究运动特征，分别位于吊臂端部（Crane Boom Tip）、钩头（Crane Hook）、桩尖 （Pile Bottom）[4]。

（1）图5展示了在工况LC1（即桩尖距泥面150 m） 时，3个代表性位置水平方向（X、Y）的运动幅度。此时钩头位于水面以下5 m范围内水溅区以下，距吊臂端部竖直距离为67 m，钩头（以短缆连于桩顶） 和桩尖的水平方向运动幅度非常大，甚至在某些来浪方向上超过吊臂端部的水平方向运动振幅（当Tp介于11～13 s范围内时）。而桩尖处运动幅度均小于钩头处水平运动幅度，表明水中质量高达700 t的钢桩起到一定的锚定作用。

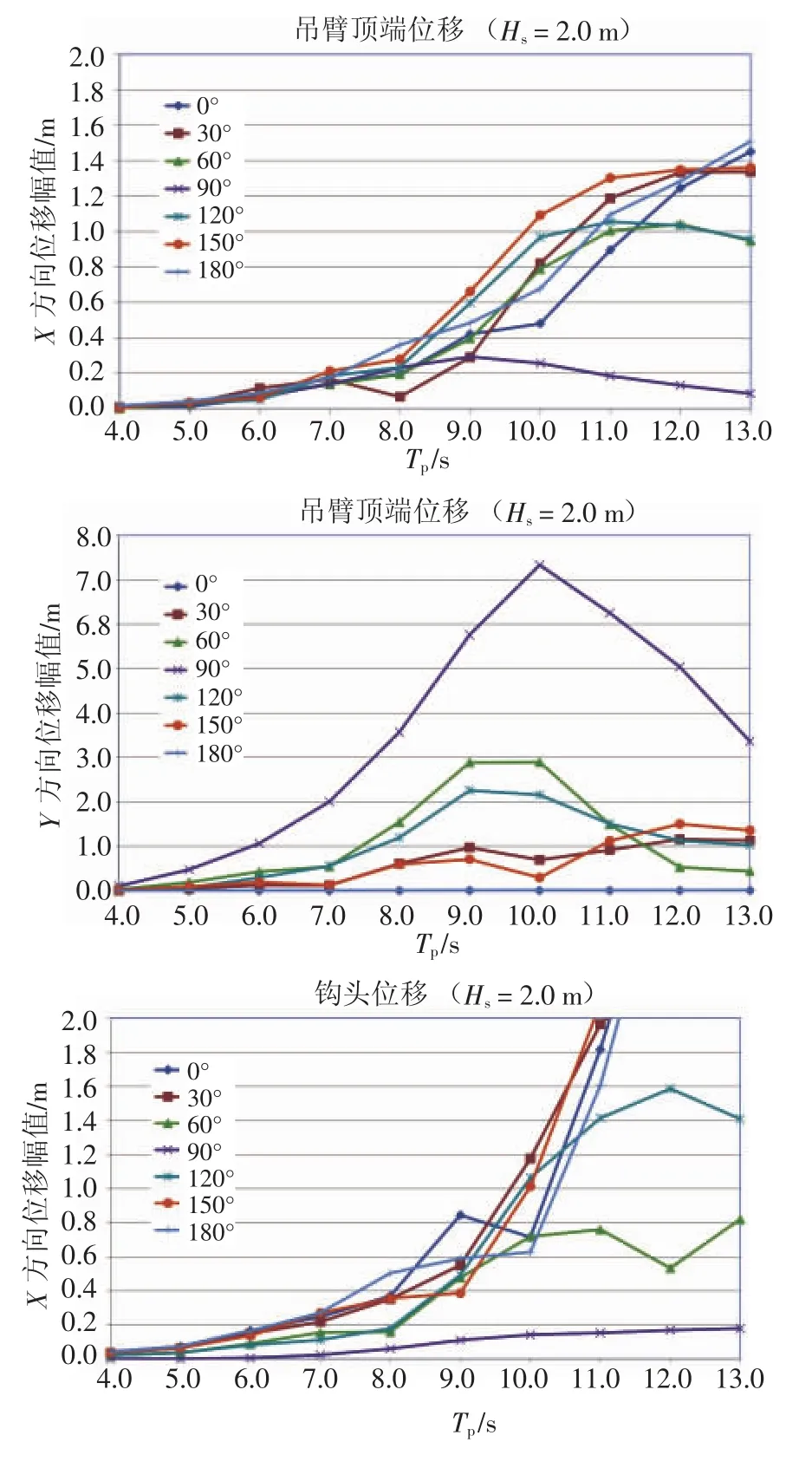
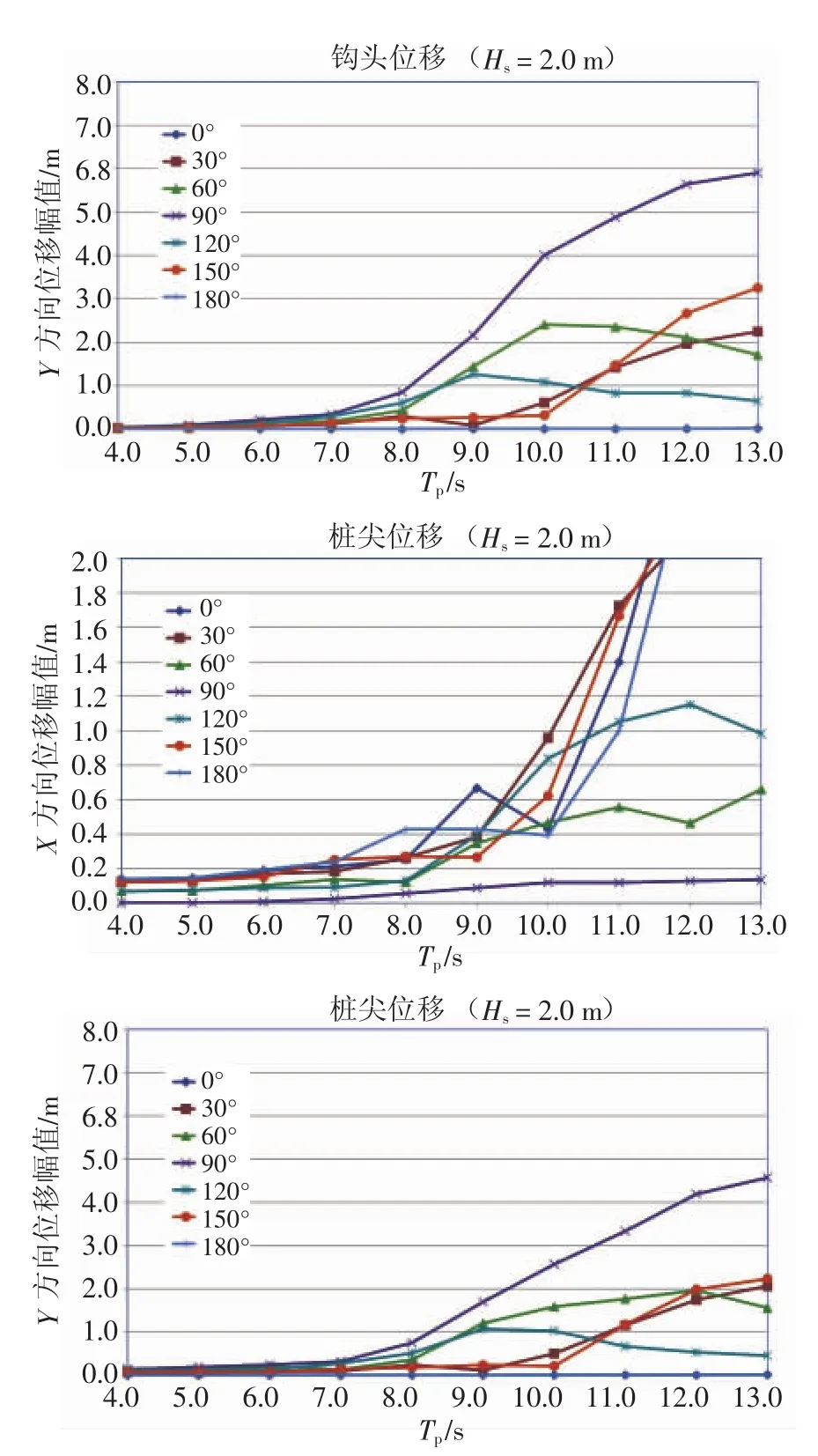
图5 工况LC1：桩尖距泥面150 m时吊臂顶端、钩头、桩尖的水平X、Y方向运动幅度

（2）作为对比，工况LC2的对应结果见图6。随钢桩下放至90 m水下，钩头和桩尖处的水平方向运动幅度迅速减小。举例来说，对桩尖位置，考虑Tp=11 s的涌浪周期，针对顺浪海况，在X方向上运动幅度由1.4 m降至0.3 m以下，而针对横浪海况，在Y方向上运动幅度由2.6 m降至1.4 m。

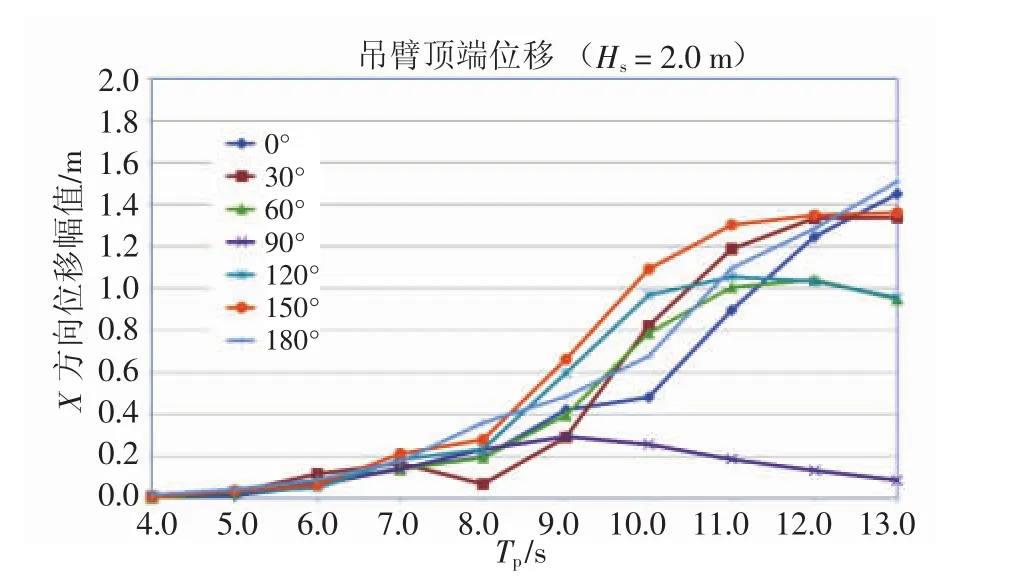
图6 工况LC2：桩尖距泥面60 m时吊臂顶端、钩头、桩尖的水平X、Y方向运动幅度

（3）当钢桩下放至桩尖距泥面30 m时（工况LC3），钢桩各处水平方向运动幅度将进一步下降。图7为3个代表性位置的水平面内的运动轨迹。钢桩的锚定作用更为明显。

图7 工况LC3：桩尖距泥面30 m时桩尖水平方向运动轨迹

2.2 竖直方向运动特征（Z）

图8、图9对比了在工况LC1（即桩尖距泥面150 m）及工况LC3（即桩尖距泥面30 m）时3个代表性位置在竖直方向（Z）的运动幅度。

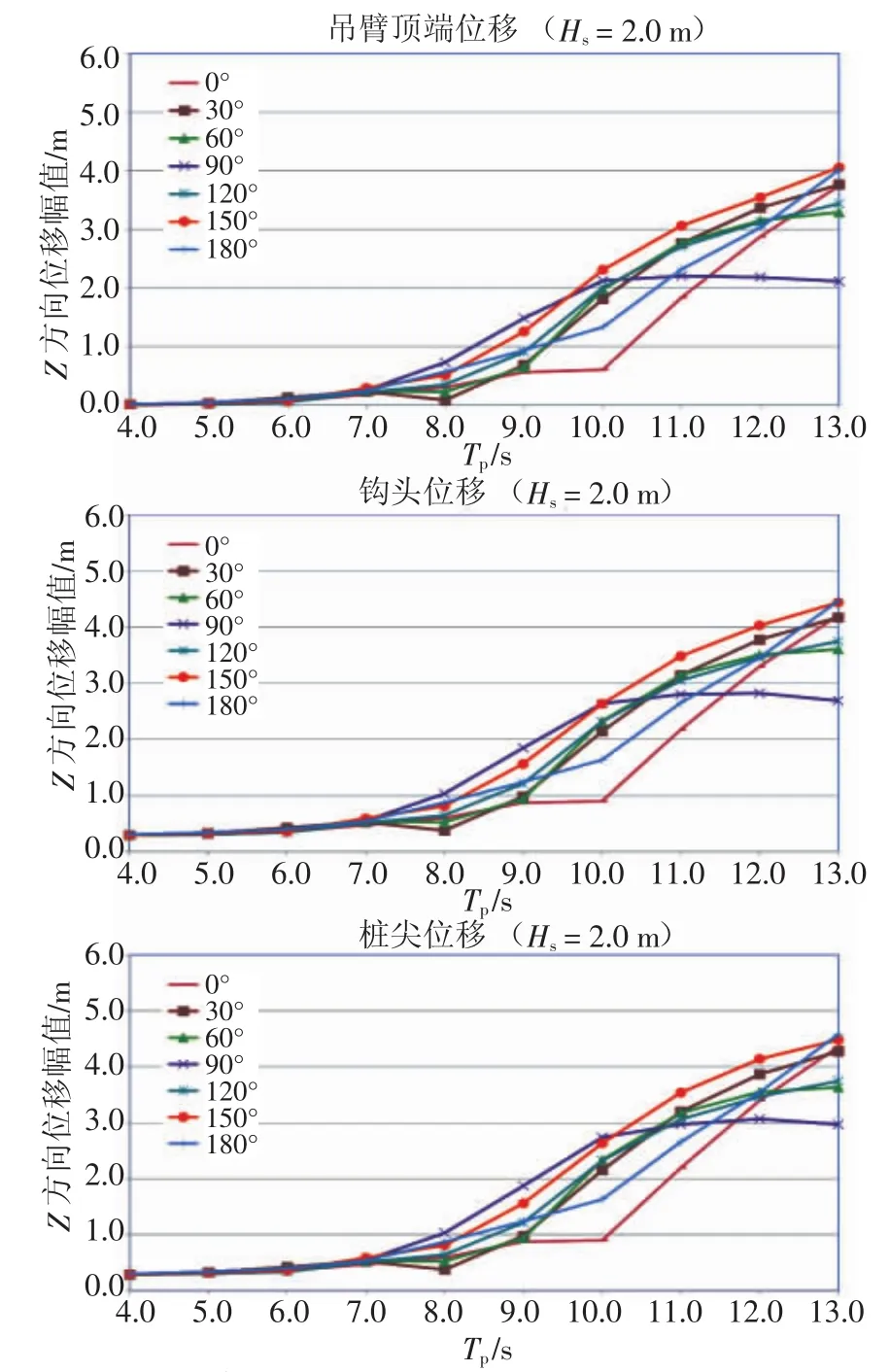
图8 吊臂顶端、钩头、桩尖的竖直Z方向运动幅度（工况LC1：桩尖距泥面150 m）

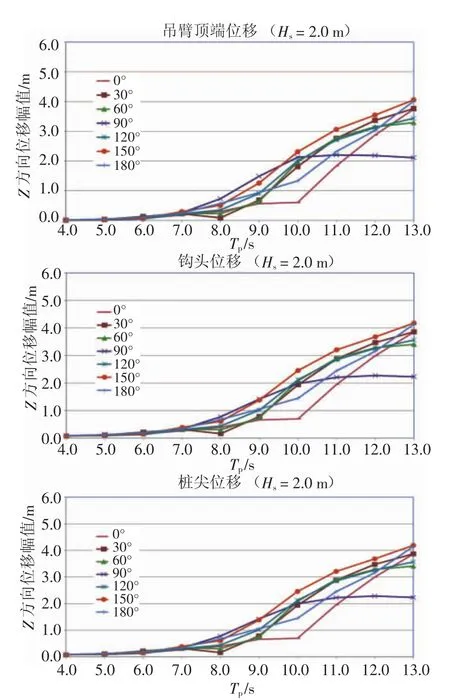
图9 吊臂顶端、钩头、桩尖的竖直Z方向运动幅度（工况LC3：桩尖距泥面30 m）

结果表明，吊臂端部、钩头（钢桩顶部）及桩尖的竖直方向运动幅度相差不大，吊臂端部的起伏直接决定了钢桩的升沉运动[5]。

2.3 来浪、来流对水平方向运动的综合影响

图10～图12为顺浪、相对船尾30°、横浪几种来浪环境工况下桩尖水平方向的运动轨迹，对应有义波高及波浪周期为Hs=2.0 m及Tp=10 s；对有无来流的工况，在同一图表上进行了对比，以揭示来流对桩尖运动的影响。

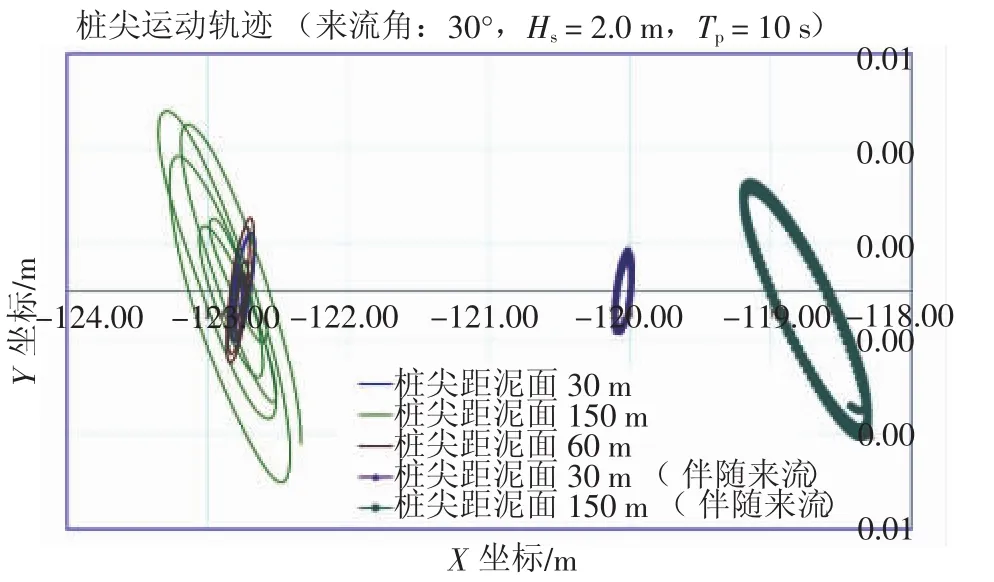
图10 顺浪（0°）环境工况下桩尖水平方向运动轨迹（包括有或无来流工况的比较）

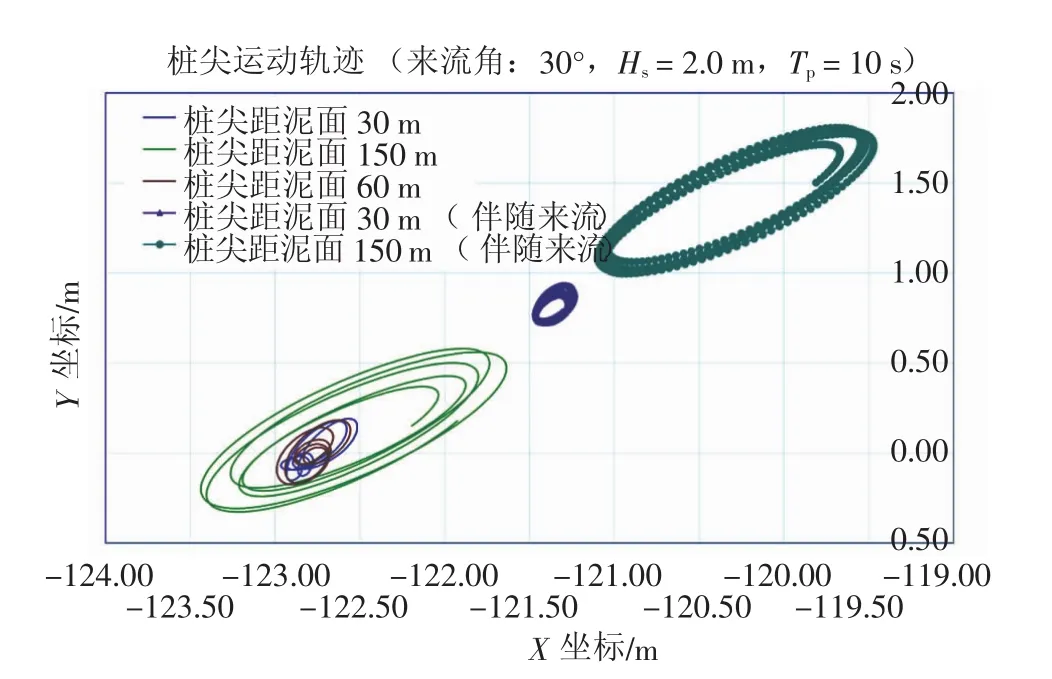
图11 船尾30°来浪环境工况下桩尖水平方向运动轨迹（包括有或无来流工况的比较）

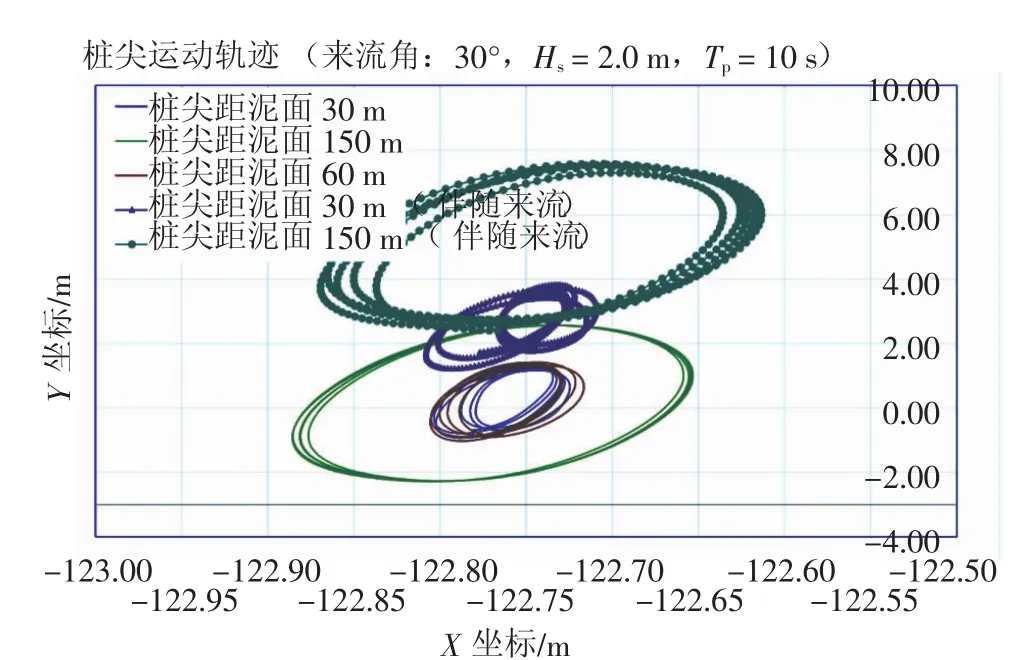
图12 横浪（90°）环境工况下桩尖水平方向运动轨迹（包括有或无来流工况的比较）

从各图上可见，对应于本工程实例1年返回期最大的流速，最大将导致约5.0 m的沿流速方向的偏移（工况LC1即桩尖距泥面150 m时），随着钢桩下放至近泥面，此偏移幅度将下降至3.0 m以内。各图的桩尖运动轨迹也再次表明了前面的研究结果，即水平方向运动幅度随着钢桩下放至泥面附近而大幅地下降。

2.4 吊装系统水平方向运动自然频率

在竖直吊装作业中，如果吊装系统某一振动模态自然频率和船体运动频率（波浪周期）比较接近，则说明存在耦合即共振的可能性[6]。在本文的工程实例中，吊装系统包括钢丝、钩头、钢桩等竖直叠加部分。在计算分析中使用Orcaflex软件对该吊装系统进行了模态分析，表3列出了对应于桩尖位于不同水深时3种工况下的前四阶振动模态的自然周期（其余为高频振动模态）。

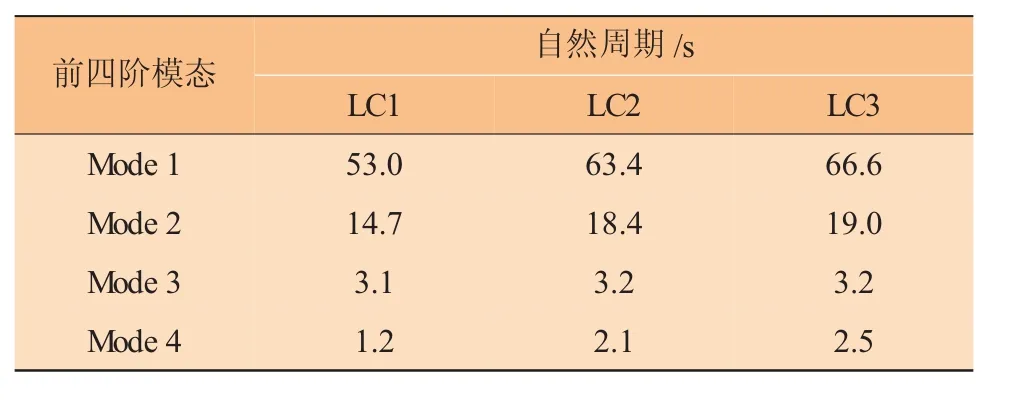
表3 桩尖位于不同水深工况（LC1、LC2、LC3）时吊装系统水平运动自然频率

表3中第二阶振动模态的自然频率与振动分析所选取的波浪周期较为接近，考虑到在波浪周期Tp=10～13 s范围内船体的运动幅度较大，而对应于LC1工况下第二阶模态的自然频率（14.7s）更为接近该波浪周期范围（Tp=10～13 s），这一对比可以用来部分解释LC1、LC2、LC3工况下水平方向的运动幅度范围差别。

3 结论

本文基于钢桩起吊和下放问题开展了数值仿真分析，揭示了吊臂端部、钩头、桩尖的运动特点，得到以下结论。

（1）对于文中深水导管架，因钢桩质量达数百吨，运动计算分析表明钢桩起到一定的锚定作用。尤其是当钢桩下放至接近泥面时，桩尖及桩顶水平运动幅度显著小于吊臂端部运动幅度，这有助于控制钢桩安装精度。

（2）在钢桩下放过程中，当钢桩刚刚没入水下时，桩尖及桩顶水平运动幅度有可能超过吊臂端部运动幅度，此时钢桩应以较快速度下放至较深水域以降低安装风险。造成这一现象的原因可能来自于吊装系统自然频率与船体运动周期的耦合，因此吊装系统的模态分析可以为钢桩运动特征提供定性判断[7]。

（3）来流速度和方向对于钢桩下放过程中的偏移影响较大，在钢桩安装分析中要考虑海浪、海流的综合影响，以控制钢桩安装精度。

（4）钢桩起吊运动特征分析有助于减小钢桩安装精度超差的风险，这对于钢桩精确下放以及后续打桩过程都很有意义。对于风电安装过程来说，进行充分的起吊下放运动分析能够有效提高安装效率，进而降低海上安装成本。