蠕变加载条件下大理岩弹性储能的演化特征

李东阳陆镜夷刘波王士杰李赛格

中国矿业大学(北京)力学与建筑工程学院,北京 100083

在地下工程中,岩石在经受长期反复的荷载作用后会出现不同程度的变形,力学性质也会有所变化。例如,在岩溶地区的岩石基础,由于岩体在长期循环荷载作用下引起地层的不均匀沉降,威胁了上部主体结构的安全[1-3]。岩石基础的受力特点主要是低应力水平条件下的蠕变过程。而在蠕变过程中,岩石对能量的吸收、转化和应变能的释放与耗散机理,目前还不是十分清楚。因此,从能量的角度来研究岩石的蠕变变形和破坏,对于深入理解岩石基础的蠕变破坏过程,改善岩石基础设计是非常有用的。

岩石的变形与破坏过程本质上是能量的演化过程。岩石在受到外力作用时,内部能量不断转换,随着弹性能的累积和耗散能的增加,岩石向着破坏的趋势发展,最终失稳破坏[4-7]。现有研究表明:不同的岩石能量演化特征在峰值前基本相似,在峰值后却有显著的差异,且耗散能系数的演化阶段与单轴压缩条件下的变形阶段密切对应[8]。这说明岩石的破坏过程一直伴随着能量转换[9-10]。在岩石受力过程中,能量的演化受到很多因素的影响,如加载条件、含水量和围压等。研究饱和岩石的单轴压缩实验发现:总应变能和弹性能与含水量呈负线性相关,而耗散能与含水量呈负指数相关[11]。在岩石破坏的过程中,弹性能增长率与加载速率呈正比关系[12]。三轴压缩条件下,岩石中的弹性应变能比与耗散应变能比呈反向变化的关系[13]。岩石在接近临界破坏点时,总应变能、弹性应变能随着初始围压的增大而增大,而耗散应变能则先增大后减小。弹性应变储能极限表现为,围压越大弹性应变储能极限越大[14-18]。

本文采用岩石三轴试验机,对饱水后的大理岩试件进行单轴循环加载和多级蠕变循环加载,获得应力-应变曲线;计算其各自的弹性能密度,对比分析大理岩长期加载条件下能量的演化特征和弹性应变储能极限的变化;以期弄清蠕变荷载条件下岩石弹性储能和演化的特征,对岩石基础长期荷载下的稳定性评估提供参考。

1 试验方法与步骤

单轴循环加载和多级蠕变循环加载试验采用冻土三轴试验机,其轴向荷载可达200 kN,荷载控制精度为0.1 kN,位移控制精度为1.0 μm。采用轴向加压控制与位移控制两种方式加载。

1.1 岩石试样

岩样为深圳地区地下10～50 m 钻探取得的大理岩岩芯,从颜色上可以分为两类,一类是白色大理岩(试样1),另一类是灰色大理岩(试样2),如图1所示。将岩石样本加工成直径50 mm、高度100 mm 的圆柱体。采用自由吸水法进行饱水处理,将水浸没试件1/3 的位置,12 h 后将水位加至2/3 高度,再过12 h 后使试件全部浸入水中,浸泡2 d 后饱水试样制作完成。

图1 X-射线大理岩岩样Fig.1 X-ray marble samples

采用X-射线衍射试验测试岩石的成分。该地区的大理岩主要是由方解石与白云石组成,试验结果见表1。白色原岩中方解石含量为100% ;灰色原岩中方解石含量为93%,白云石含量为7%。因此,方解石晶粒以及晶粒间的相互作用对该区域的微风化大理岩的物理力学性质起控制作用,白云石晶粒只起辅助作用。通过单轴压缩试验,测试得到该大理岩饱和单轴抗压强度平均值σc=67.36 MPa,弹性模量平均值E=42.50 GPa。

表1 大理岩岩样X-射线衍射分析Table 1 X-ray diffraction analysis of marble samples

1.2 单轴循环加卸载试验

为对比大理岩在蠕变加载条件下的弹性能密度及弹性储能极限是否发生变化,进行单轴循环加卸载试验。试验加卸载路径如图2所示,步骤如下:

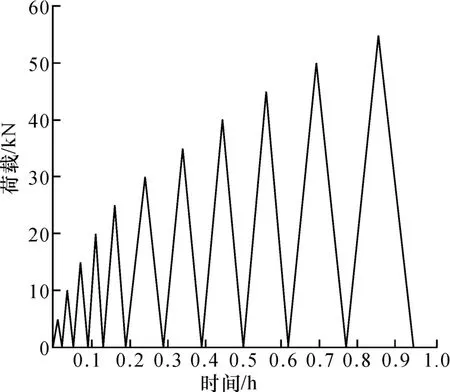
图2 大理岩加卸载方式Fig.2 Loading and unloading path of marble samples

(1) 设置三轴压缩试验机自动加卸载程序,每级荷载为5 kN,加载速度为200 N/s。

(2) 试验机从0 kN 开始加载至5 kN,达到预定荷载后卸载至0 kN,完成第1 次加卸载;然后从0 kN 加载至10 kN,达到预定值后卸载至0 kN,完成第2 次加卸载。如此循环加卸载,直到试件破坏。

共进行4 个大理岩单轴循环加载-卸载试验,试件A2 的应力-应变曲线如图3所示,其他试件的应力-应变曲线与试件A2 类似。其中,单次加卸载弹性能密度计算示意图如图4所示:应力达到σ1时卸载,对应的应变为ε1,卸载到0 时,残余形变为ε0。外力做功输入的总能量为U。假设岩石变形与破坏的过程中与外界不发生热交换,根据热力学第一定律可知[19]:

图3 大理岩单轴循环加卸载的应力-应变曲线Fig.3 Stress-strain curve of marble sample under uniaxial cyclic loading and unloading

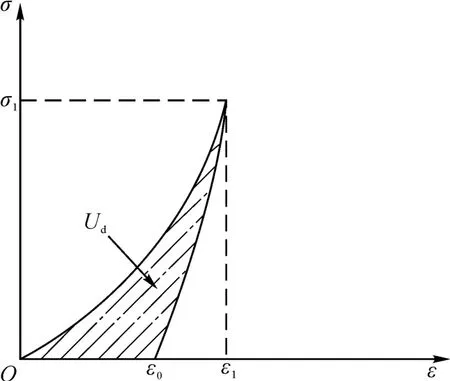
图4 岩样单次加卸载弹性能密度计算示意图Fig.4 Calculation diagram of elastic energy density under single loading and unloading for rock sample

式中,U为外力对大理岩做的总外力功密度,由加载曲线与应变轴围成的面积得出;Ue为储存在大理岩内部的弹性能密度,由卸载曲线与应变轴围成的面积得出;Ud为耗散能密度,由U与Ue两者之差计算得出。

计算得到外力对每个大理岩试件做的总外力功密度U,大理岩的弹性能密度Ue以及耗散能密度Ud。试验结果见表2,岩样破坏结果如图5所示。

图5 单轴循环加卸载下大理岩试件破坏形态Fig.5 Failure modes of marble samples under uniaxial cyclic loading and unloading

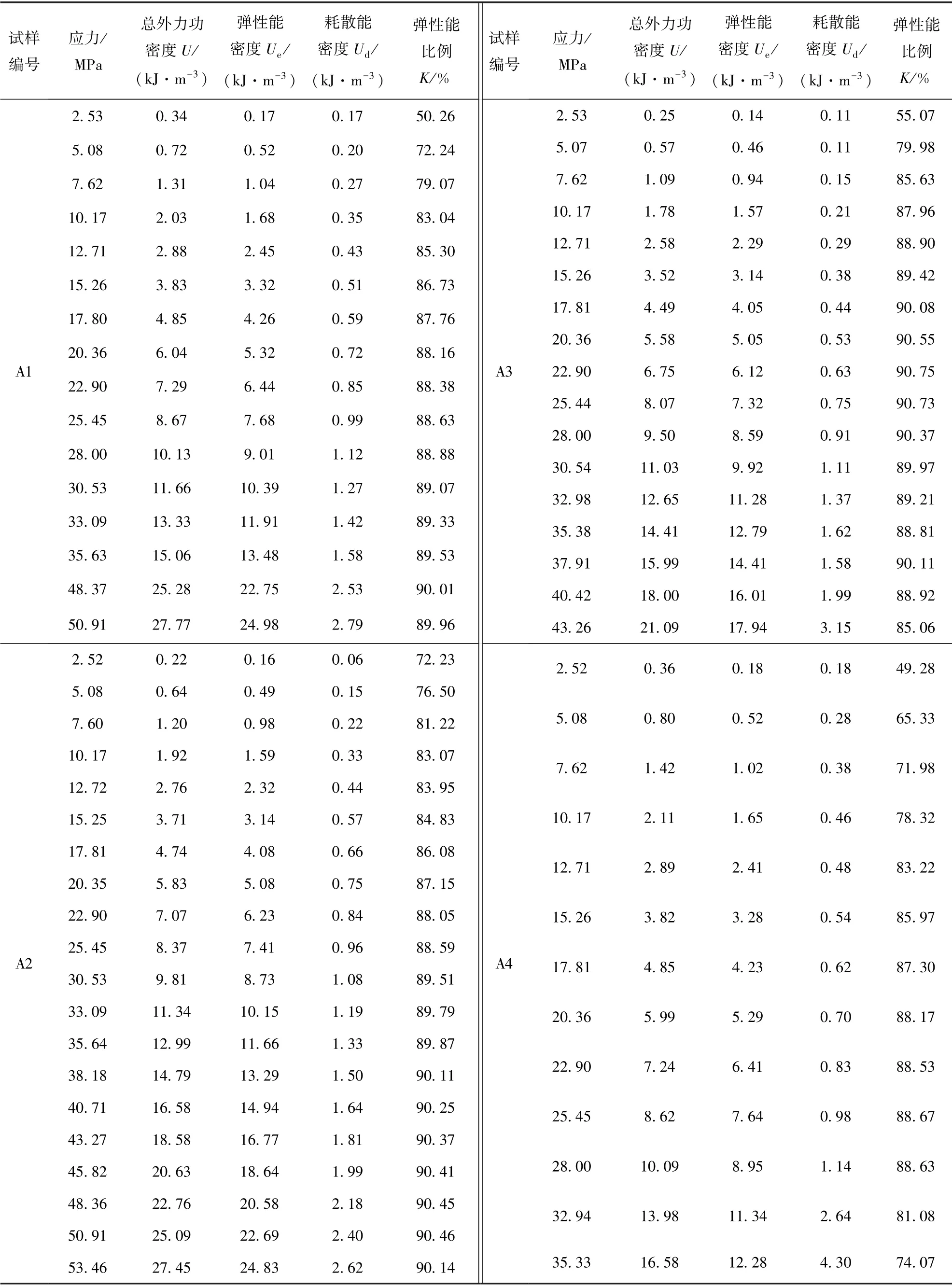
表2 单轴循环加卸载试验结果Table 2 Test results of uniaxial loading and unloading cycles

1.3 多级蠕变循环加卸载试验

单轴循环加卸载试验只能了解岩石在循环加卸载过程中能量的变化,并不能反映蠕变过程是否对能量演化造成影响,因此需要进行多级蠕变循环加卸载试验。试验步骤如下:

(1) 首次试验荷载为3.39 MPa,是大理岩单轴抗压强度平均值σc的5%,先进行1 次单轴加卸载,再进行蠕变加载试验12 h,之后卸载。

(2) 分别进行应力为10%σc,15%σc,20%σc……的蠕变加卸载试验,直至试件破坏。加卸载循环方式如图6所示。

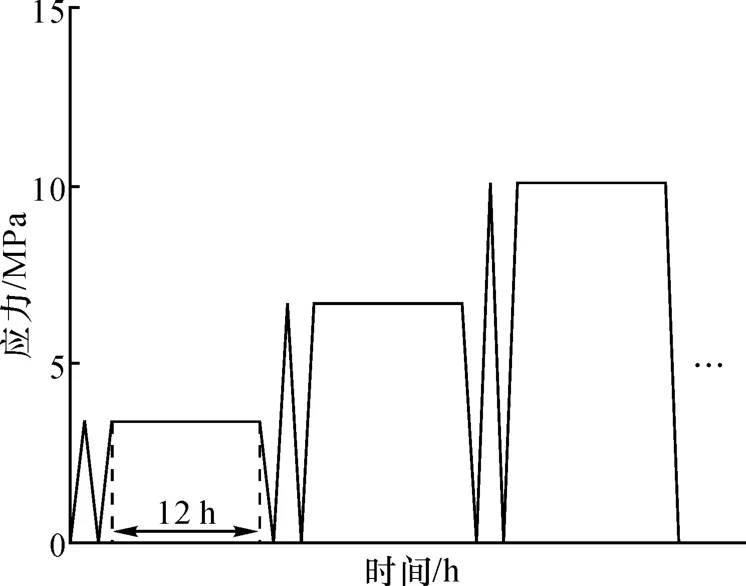
图6 大理岩岩样多级蠕变循环加卸载模式示意图Fig.6 Schematic diagram of marble sample under multi-level creep cyclic loading mode

共进行4 组大理岩多级蠕变加卸载试验,试样B2 的应力-应变曲线如图7所示,其他试件的应力-应变曲线与试件B2 类似。其中大理岩蠕变加卸载一次循环示意图如图8所示。先加载到σi,然后迅速卸载到0,测得岩样的弹性能密度Ue1,随即再次加载到σi,保持σi应力状态12 h,再卸载到0,测得蠕变后岩样的弹性能密度Ue2。σi为第i次加载等级。循环包括2 个阶段:第1 阶段为加载曲线1-卸载曲线1 阶段;第2 阶段为加载曲线2-保持荷载曲线-卸载曲线2 阶段。后面各次循环加卸载步骤与之类似。计算每次循环中的第1 阶段和第2 阶段的能量密度。计算结果见表3,岩样破坏结果如图9所示。

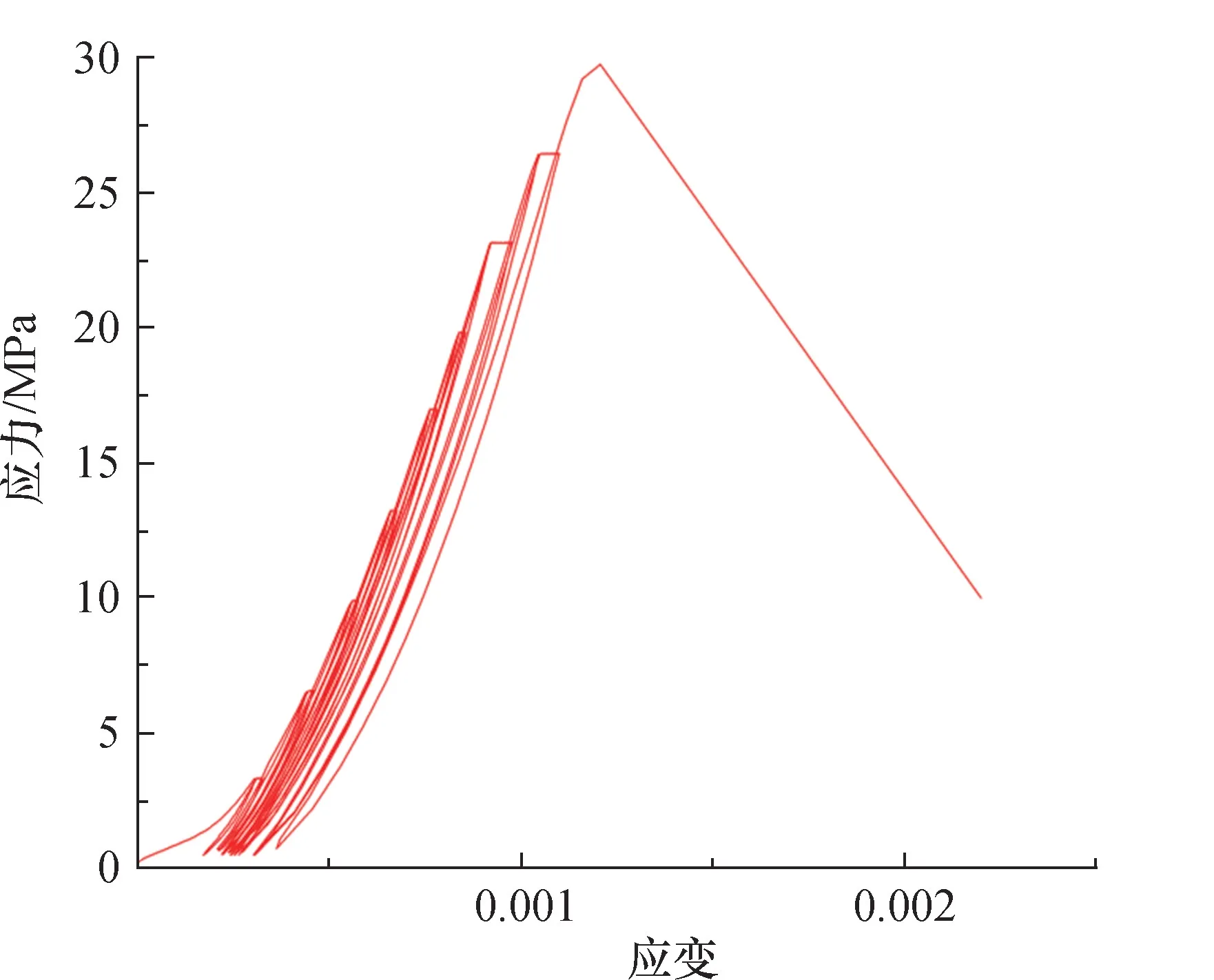
图7 大理岩多级蠕变循环加卸载试验应力-应变曲线Fig.7 Stress-strain curve of marble sample under multi-level creep cyclic loading and unloading

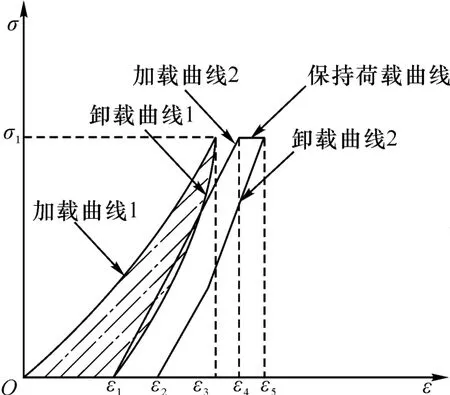
图8 大理岩试样单次蠕变加卸载应力-应变关系示意图Fig.8 Relationship diagram between stress and strain of marble sample under single creep loading and unloading

图9 多级蠕变循环加卸载下大理岩试件破坏形态Fig.9 Failure modes of marble samples under multi-level creep cyclic loading and unloading

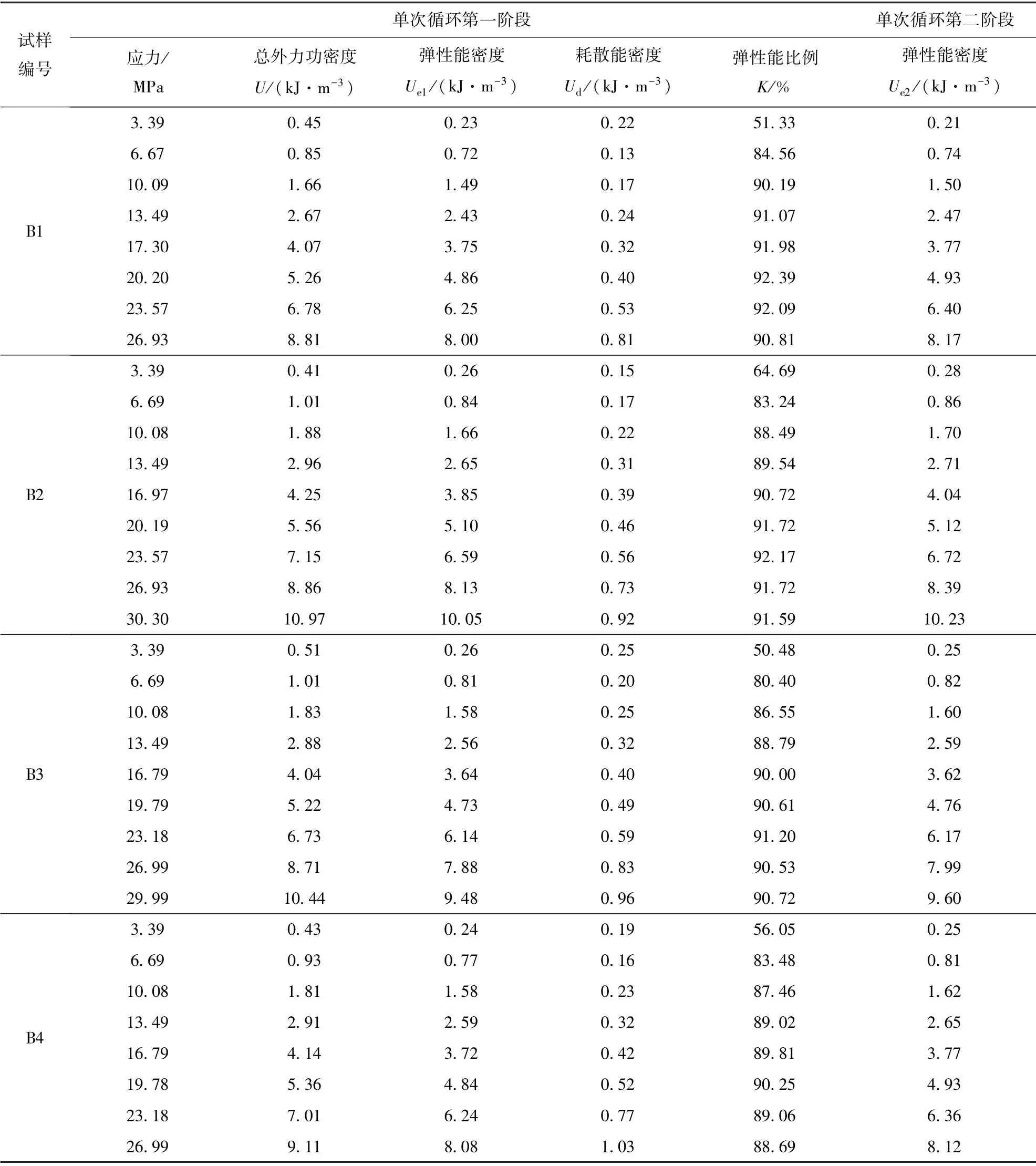
表3 多级蠕变循环加卸载试验结果Table 3 Test results of multi-level creep cyclic loading and unloading

2 试验分析与讨论

为分析蠕变加载对大理岩储能极限的影响,对2 种加载方式的试验结果进行对比,讨论弹性能密度曲线的形式,并结合大理岩破坏过程探寻储能极限变化的原因。

2.1 弹性能密度曲线的形式和参数拟合

对试验结果进行处理,得到2 种加载模式下的弹性能密度曲线,如图10所示。观察可知:2 种加载模式下弹性能密度曲线大致相同,这说明无论是蠕变加载模式还是单轴循环加载模式,都不影响材料的弹性能密度曲线。随着应力的增加,弹性能密度逐渐增大,即随着外部力对大理岩做功,储存在大理岩内部的弹性能密度越来越大。因此,根据曲线形状采用幂函数对弹性能密度曲线进行拟合,拟合结果见表4和表5。

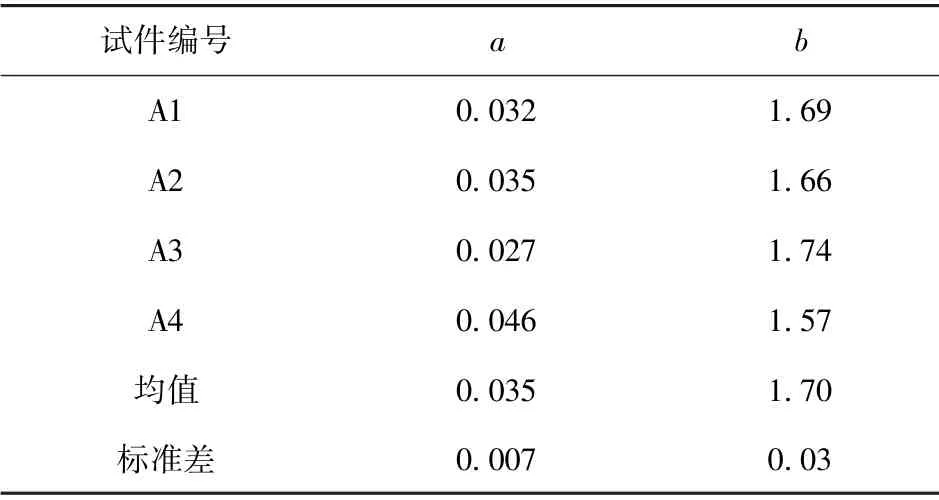
表4 单轴循环加载拟合的参数a 与bTable 4 Fitting parameters a and b by uniaxial cyclic loading

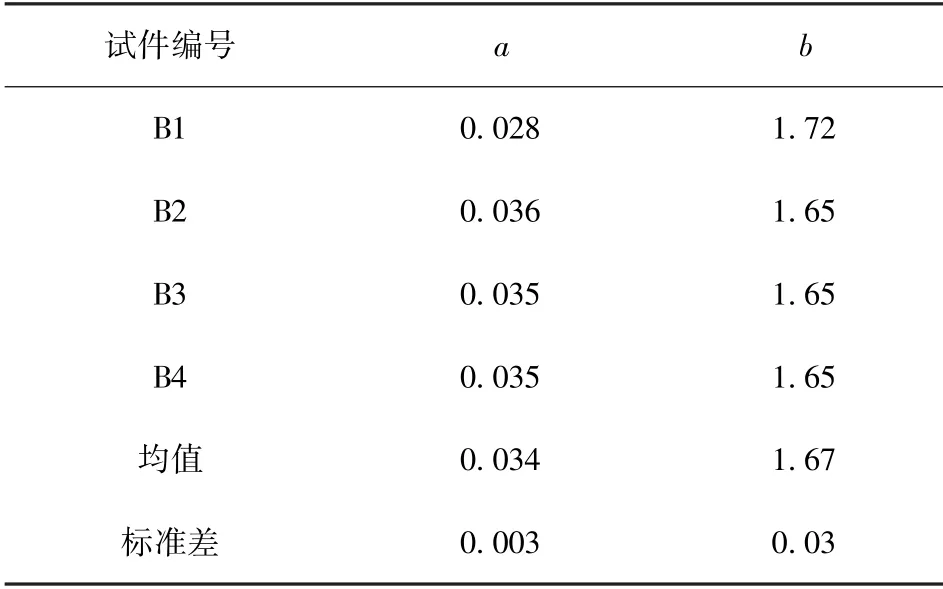
表5 蠕变循环加载拟合的参数a 与bTable 5 Fitting parameters a and b by creep cyclic loading

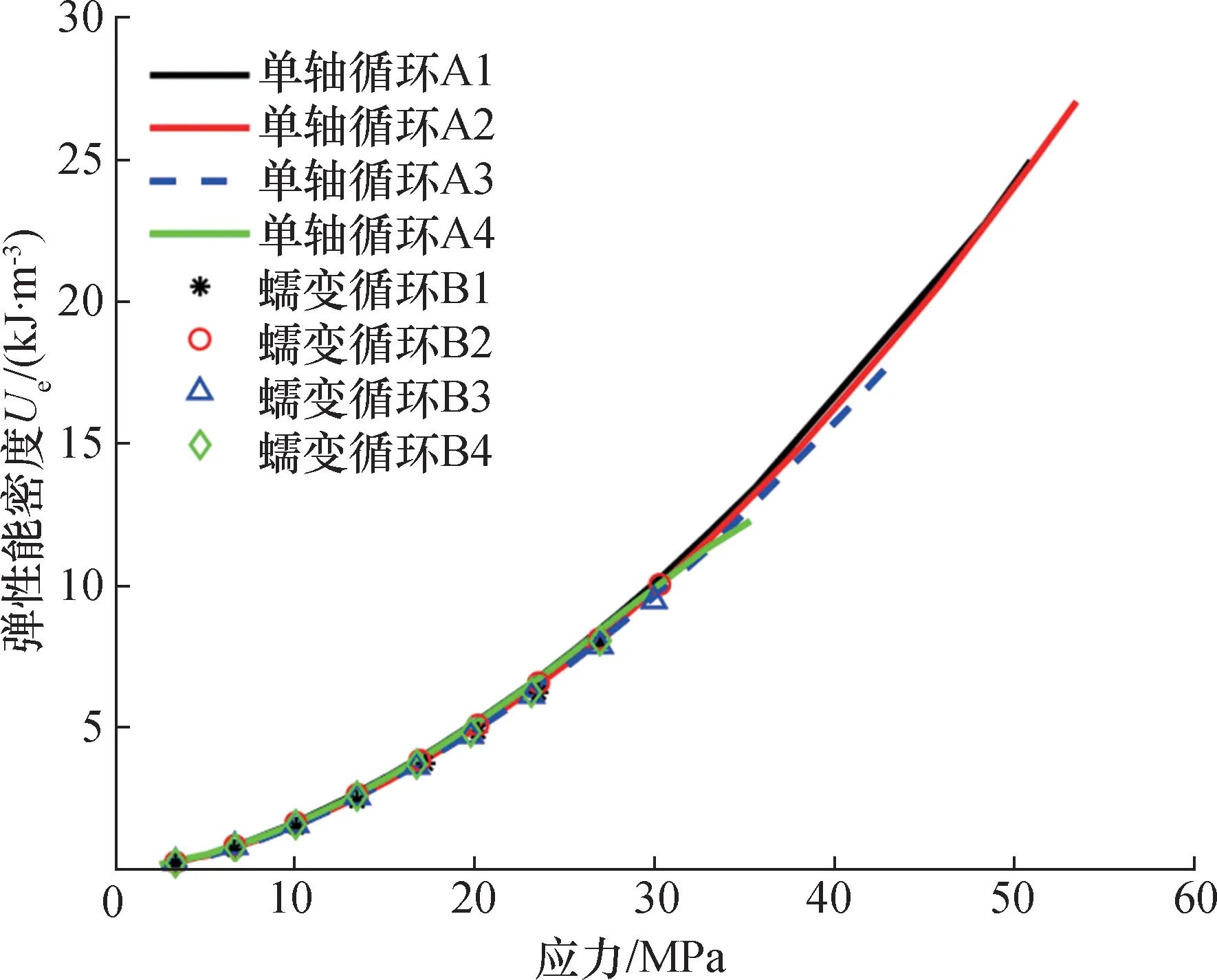
图10 2 种加载模式下的弹性能密度曲线Fig.10 Elastic energy density curves under two loading modes

式中,Ue为弹性能密度;σ为应力;a和b为拟合函数的参数。

根据表4和表5,2 种加载模式下拟合函数的参数a和b的平均值及标准差很小,说明大理岩应力-弹性能密度曲线离散程度较低。幂函数能较好地表达大理岩弹性能密度与应力之间的关系。

弹性能密度还可以由理论公式计算获得,假设材料为弹性,则弹性应变能密度Ue为

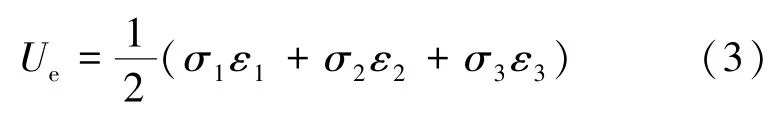
在单轴压缩实验中,σ2=σ3=0,代入式(3)可得

假设加卸载过程中材料的弹性模量E始终不变,则由广义胡克定律知:

将式(5)代入式(4)得

将单轴压缩试验得出的弹性模量平均值E=42.5 GPa 代入,则有

以A3 为例,理论计算曲线与试验拟合曲线对比如图11所示。由图11可知,拟合曲线与理论计算曲线大致重合,采用幂函数Ue=aσb能很好地拟合大理岩弹性能密度Ue与应力σ之间的数学关系。这与假设材料为弹性条件的理论计算公式Ue=σ2/2E在形式上是相同的。

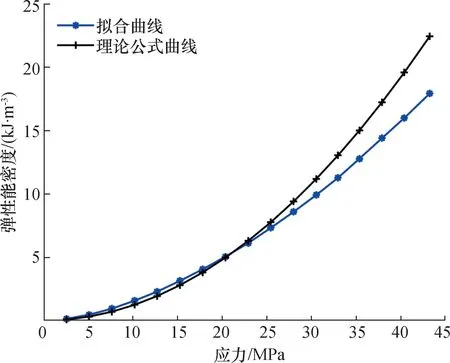
图11 A3 试样的拟合曲线与理论计算曲线Fig.11 Fitting curve and theoretical calculation curve of A3

实际上,大理岩材料有一定的非线性弹性,所以试验结果显示a与及b与2 都有一定偏差,但较为接近。试验结果符合线弹性材料卸载服从胡克定律的约定。

2.2 大理岩储能极限和强性能比例的变化

大理岩的储能极限即大理岩最大存储弹性能密度的能力。储能极限取值是试件破坏前最后一次循环对应的弹性能密度。弹性能比例K即弹性能密度占总外力功密度的百分比。为探究蠕变加载对大理岩储能极限的影响,本文计算并分析了大理岩在单轴循环加载与多级蠕变循环加载状态下的储能极限值(表6)。

由表6可知:大理岩在多级蠕变循环加载状态下,破坏时极限弹性能密度平均值为8.90 kJ/m3,而在单轴循环加载状态下的极限弹性能密度平均值为20.57 kJ/m3,即经过蠕变之后,大理岩储存弹性能的能力约为单轴循环加载的43%。破坏时的应力平均值由45.74 MPa 下降到28.55 MPa,约为单轴循环加载强度的62%。

表6 弹性能储能极限值Table 6 Limit value of stored elastic energy

绘制2 种加载模式下大理岩弹性能比例与应力的关系曲线,如图12所示。为避免曲线过多引起混乱,这里仅绘制单轴循环加载的A1、A2 试样和蠕变循环加载的B1、B2 试样做对比。根据表2和表3绘制2 种加载模式下的耗散能密度曲线,如图13所示。

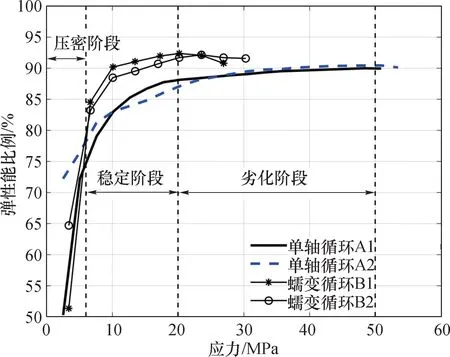
图12 大理岩在2 种加载模式下弹性能比例曲线Fig.12 elastic energy ratio curves of marble under two loading modes

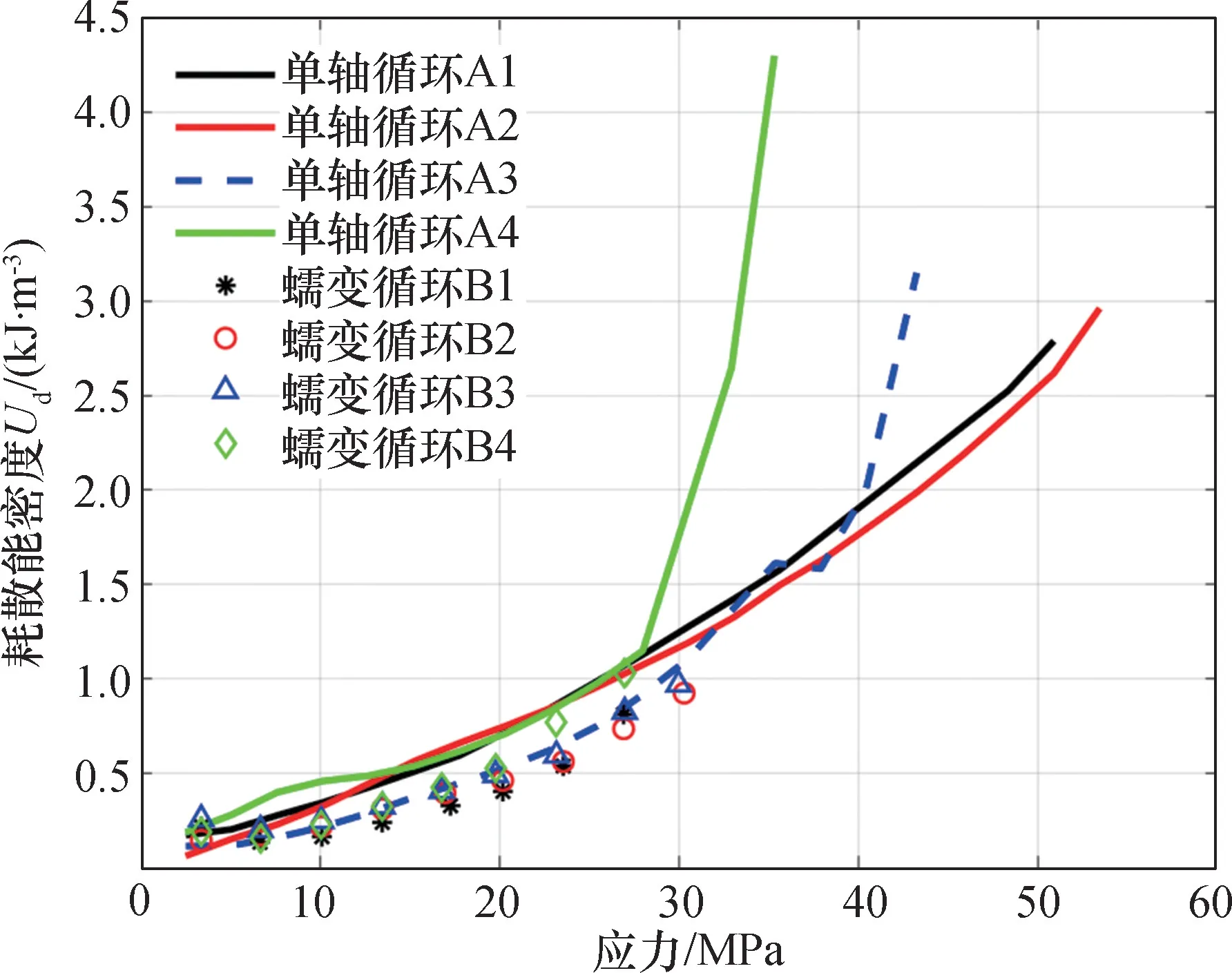
图13 大理岩在2 种加载模式下的耗散能密度曲线Fig.13 Dissipative energy density curves of marble under two loading modes

由图12和13可知:

(1) 经历循环蠕变荷载之后的大理岩,其强度和承载能力都有明显下降。究其原因,大理岩在长期外部荷载作用下,外力做功产生的大部分能量被耗散,耗散的能量主要用于大理岩产生裂隙,裂隙贯通使得大理岩完整性降低,内部微裂隙不断发展,最终使得其极限弹性能密度大大降低,岩石更容易被破坏。

(2) 2 种加载模式下的大理岩能量演化特征都经历3 个阶段:

①压密阶段:在应力小于5 MPa 时,2 种加载模式下弹性能比例随应力的增加均呈现急剧增长的趋势,此时大理岩处于逐渐压密的过程,应力长期作用下,使得大理岩内部孔隙逐渐闭合。随着应力的增加,外力功转化为弹性能的比例逐渐增大。因此,该阶段外力的增加使大理岩的材料力学性质逐步优化。考虑该种大理岩的长期承载能力,其最大应力值应控制在5 MPa 以下。

②稳定阶段:压密阶段后,当应力继续增加10～20 MPa 时,弹性能比例逐步稳定。单轴加卸载条件下,弹性能比例稳定在85%～88% 之间;在蠕变循环荷载加载条件下,弹性能比例稳定在90%～93% 之间。此时大理岩在较大应力作用下,内部孔隙已经处于压密状态。随应力的增加,大理岩变得更加密实。

③劣化阶段:对于单轴加卸载试样,当应力超过20 MPa 且继续增大之后,弹性能比例却稳定在88%～90% 之间,表明外力再继续增加时,大理岩中的耗散能密度将增大,外力做功产生的耗散能使大理岩产生更多的裂纹,逐渐贯通成为裂隙,直至大理岩发生破坏。说明在远低于大理岩单轴抗压强度平均值(67.36 MPa)的应力条件下,其材料性能就开始劣化了。

3 结 论

(1) 单轴循环加载试验和多级蠕变循环加载试验的弹性能密度曲线基本重合,二者具有相同的弹性能密度曲线。区别在于,经历反复蠕变荷载之后的大理岩,单轴抗压强度明显降低,为单轴循环加载条件下的62%,弹性储能能力也明显降低,仅为单轴循环加载条件下的43%。说明蠕变循环可以增加损伤的发展,明显降低单轴抗压强度,自然也明显降低其储能极限。

(2) 采用幂函数Ue=aσb能很好地拟合大理岩弹性能密度Ue与应力σ之间的关系。这与假设材料为弹性条件的理论计算公式Ue=σ2/2E在形式上是相同的。实际上,大理岩材料有一定的非线性弹性特征,所以试验结果显示a与及b与2有一定的偏差。但试验结果大致符合线弹性材料卸载服从胡克定律的约定。

(3) 两种加载模式下,大理岩材料均经历压密、稳定和劣化3 个阶段。如果考虑该种大理岩的长期承载问题,其最大应力值应控制在材料的压密阶段结束点对应的应力以下。