桥梁冲刷深度计算方法评价及基础合理埋置深度研究

胡峰强，陈家俊，胡思聪，王靓妮

(南昌大学 建筑工程学院，江西 南昌 330031)

0 引言

桥梁在服役期间往往受到各类环境因素的作用，导致其耐久性和安全性下降。其中，水流冲刷是造成桥梁损坏的重要因素之一。我国大多数桥梁水毁事件是因为桥梁墩柱的冲刷导致基础埋置深度减小，桩基的承载力下降所导致的[1]。近些年，桥梁墩柱因冲刷所导致的桥梁水毁事件频频发生，美国统计了1989—2000年之间的503 座失效桥梁，发现超过50%是由冲刷引起[2-3]。2010年我国四川的三渡水大桥因墩柱受水流冲刷引起基础掏蚀，导致基础埋置深度减小造成墩柱倾斜最后垮塌，此次事件对当地的交通和经济都造成了一定的影响。2016年闽清县山区42座桥发生了墩台基础冲刷损坏，此次事件不仅威胁到了人民的生命安全，对当地的经济也造成了一定的损失。

为了避免桥梁在冲刷作用下发生破坏，设计中需要根据桥梁的冲刷深度确定基础的最小埋置深度。因此，准确预测桥梁冲刷深度是桥梁设计中的重要环节。然而由于冲刷机理的复杂性，导致没有单一的解析推导公式可用[4]。Melvile等[5]对桥梁冲刷深度预测公式进行了早期的总结，使用阈值法结合试验数据对预测公式的系数进行调整，并得到了不同系数的适用范围，然而此方法被相关学者认为其结果过于保守。Cardoso等[6]对Melvile等[5]试验中使用的矩形水槽进行了改进，使用一种两级通道，桥台使用不同的距离延伸到洪泛区上直至主通道边缘。Faruque Mia等[7]根据输沙平衡理论结合试验数据提出在输沙理论中应考虑圆桥墩床剪应力的变化。Giuseppe Oliveto等[8]利用相似参数和流动阻力的类比，提出了一个冲刷随时间的演化方程，并利用大量的文献数据进行了验证，但此次研究没有考虑黏度因素。Giuseppe Oliveto等[9]通过大量试验对阈值Froude数和其他影响局部冲刷进展的重要参数进行了研究，对已提出的Giuseppe Oliveto[8]研究结果进行扩展。Harrsi等[10]对一种工程模型的发展进行了研究，围绕在电流、波和组合波流下的海洋结构预测冲刷演变与时间的关系，该模型强调了与冲刷预测有关的多方面问题。Reza Mohammadpour等[11]使用多元线性回归(MLR)、基因表达规划(GEP)和人工神经网络(ANN)，采用EED前馈反向传播和径向基函数预测短桥台处冲刷深度随时间的变化，提出了一种冲刷深度预测公式。Sung-Uk Choi等[12]的研究提出了一种利用维数分析和非线性回归分析所得到的局部冲刷与时间的关系。

不同的研究方法给冲刷深度的研究提供了不同的思路和方法，然而因为影响因素重要程度和适用范围的差异，导致这些预测方法都存在一定的局限性，与实际工程的衔接还需进一步研究。所以现阶段在冲刷深度预测公式的使用上缺乏合理的选取方法，这给桥梁设计带来了较大的影响。

本研究对现阶段常用的桥梁冲刷深度计算方法进行总结，在此基础上使用FLOW-3D软件进行建模，得到不同影响因素下的墩柱冲刷深度，将其结果与预测公式计算结果进行对比、评估，得到建议选用公式后，联合最大包络原则得到基础合理埋置深度的拟合多项式。

1 常用冲刷深度预测模型

1.1 Melville模型

1988年，Melville等[5]提出了一种计算桥墩局部冲刷平衡深度的设计方法，该方法基于实验室实时试验数据，绘制包络曲线。试验数据采集包括流速、深度、泥沙尺寸、泥沙级配、桥墩尺寸以及形状的广泛变化，研究提出的冲刷深度计算公式为：

(1)

式中，ds为平衡冲刷深度；D为墩柱直径；KI为水流强度；Ky为水流深度；Kd为泥沙粒径；Kσ为泥沙级配；Ks和Kα为桥墩形状线性系数。每个参数都被单独考虑，参数的取值通过试验结合理论得到。此次的研究得到Kσ=1.0，Ks和Kα为常数。本研究的研究以式(1)及Jihn-Sung Lai等[13]在2009年提出的最大冲刷深度预测为基础进行研究。

1.2 Cardoso模型

Cardoso等[6]在1999年对桥台局部冲刷进行了试验研究。试验在两级渠道中进行，将桥台延伸到漫滩上的不同距离，包括一直延伸到主渠道边缘的情况。此次研究测量了时间演变下的最终冲刷深度,提出了一种冲刷深度预测公式：

(2)

式中dst为t时刻的冲刷深度；dse为冲刷平衡时的冲刷深度，a1=-0.028，a2=1/3；t为冲刷经历时间；L为墩柱直径;U同上。

1.3 Faruque Mia模型

2003年，Faruque Mia等[7]提出了一种预测局部冲刷深度随时间变化规律的计算方法。此研究在均匀河床上设置圆柱墩进行试验，根据泥沙输移方程计算桥墩冲刷深度，发现当河床剪应力趋于冲刷坑中的临界河床剪应力时达到平衡冲刷深度。因此，认为在圆形桥墩冲刷研究中应纳入泥沙输移理论，该方法跟踪了不同来源的试验数据，提供了一种冲刷深度的计算方法：

(3)

式中，dst为t时刻的冲刷深度；θ为冲止角；D为圆形墩柱直径；qsti为第i阶段的沉积物体积迁移率。此方法参考Kothyari等[14]提出的一个经验公式描述桥墩前端河床剪应力的时间变化。假设涡旋下的剪应力随初生涡旋横截面积的增大而减小[15]，当U/Uc>0.5或U*/U*c>0.5时，墩头冲刷开始。U和U*分别是未受干扰的平均接近速度和平均接近剪切速度[16]。

1.4 Giuseppe Oliveto模型

Giuseppe Oliveto等[8]基于瑞士苏黎世ETH收集的大量数据，对桥梁墩台冲刷进行了新的研究。共测试了6种不同的沉积物，特别提到了黏度的影响，并将其排除在所提出的方程中。同时提出，对于接近尾端的冲刷条件，最大冲刷深度几乎呈线性变化；在一定范围内，本研究的结果可应用于实践。

(4)

式中，Z为无量纲冲刷深度，z为t时刻冲刷深度；桥墩为圆柱形时zR=(h0D2)1/3；矩形桥台时使用zR=(h0b2)1/3；N=1或N=1.25分别为圆柱形桥墩和立式桥台的形状系数；σ=(d84/d16)1/2为泥沙均匀性参数；T=t/tR为相对时间。

1.5 Harrsi模型

Harrsi等[10]在2010年通过建立冲刷模型，该模型可以预测在海流、波浪和波流联合作用下，海洋结构物周围冲刷随时间的演变过程。该模型已经针对一系列数据进行了测试，并且进行了理想化测试。虽然该模型在近海风力涡轮机研究中具有明显的作用，但它并不局限于这一领域，可应用于桥梁冲刷情况或其他单桩结构周围冲刷的情况。通过模型模拟计算，联系潮汐作用提出了新的墩柱结构冲刷深度的预测公式：

(5)

式中te为达到平衡的冲刷时间；n=1，参考Sumer等[17]的研究；其他参数同上。

1.6 Reza模型

Reza Mohammadpour等[11]在2013年通过试验研究了清水条件下直立墙桥台局部冲刷的尺寸及其随时间的变化规律。采用多元线性回归(MLR)、基因表达规划(GEP)和人工神经网络(ANNs)、前馈反向传播和径向基函数对短桥台冲刷深度随时间的变化进行了预测。试验研究提出了一种冲刷深度预测公式：

(6)

式中各符号意义与前相同。

1.7 Lanca模型

Lanca 等[18]通过新模型的建立以及对数据的优化处理，研究得到了式(2)中的a1和a2更新的理论计算方法：

(7)

(8)

1.8 David J. McGovern模型

David J. McGovern等[19]通过室内水槽试验研究了在潮流作用下，作为海上风电机组单桩缩尺模型的垂直圆筒周围冲刷随时间的发展,此次研究考虑了墩柱在水流作用下的冲刷作用，并对随时间变化的冲刷深度进行预测，使用的预测公式为桥梁冲刷深度随时间变化的公式，参考Sumer等[17]、Melville等[20-21]、Chiew等[22-23]及Rigin等[24-25]相关的研究成果。此次研究使用的冲刷平衡深度计算公式为：

(9)

式中，dsc=随时间变化的冲刷深度；Uc，U，te与前面公式中含义相同，使用Melvile等[17]提出的方法进行计算；dsce为冲刷平衡时的冲刷深度，其研究通过试验结合实际得出新的计算公式为：

(10)

式中,K1～K3分别为修正系数，K1为形状修正系数(当墩柱为圆柱形时为1)；K2为冲止角修正系数(当墩柱为圆柱形时为1);K3为河床参数为1.1。试验表明，不同水深对冲刷深度的影响小于10%。此研究在这些限值范围内对单向和反向水流试验冲刷深度进行了比较。

1.9 Sung-Uk Choi模型

2016年，Sung-Uk Choi等[12]利用量纲分析和非线性回归，提出了时间与局部冲刷的关系式。其研究结果表明，所提出的关系式比现有的公式更能预测随时间变化的局部冲刷。所提出的关系式适用于圆柱桥墩周围的局部冲刷：

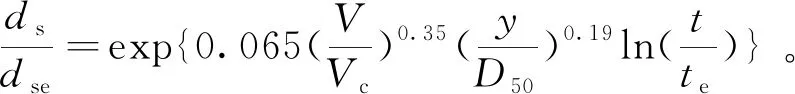
(11)

2 模型建立

此次研究使用FLOW-3D建立桥梁墩柱冲刷模型，得到有限元模拟结果，再根据多种预测公式的计算结果进行相关性检验，得到各公式的使用建议。首先进行模型的建立。

FLOW-3D模型的建立：重力加速度取-9.81 m/s2，选择RNGk-ε重整化群模型，计算终止时间根据2017年Aysegul等[26]的研究进行选取，计算时间初始步长为0.01 s，计算使用最小计算步长为10-7s。水流深度根据数值模拟要求结合实际工程进行取值。对网格的计算数量和计算精度综合考虑单元网格尺寸设置为0.2 m×0.2 m，压力迭代使用GMRES算法。墩柱、河床和挡块的建立如图1中(a)所示，图中阴影部分为挡块，挡块为刚体，其设计目的是为了将进水流处超出河床部分的水流进行阻挡，避免造成模拟结果不准确。图1中(b)图为网格划分示意图，实际网格划分以实际建模为准；模型水流进水口和出水口为对立面，底部使用无滑移或局部滑移边界条件，剩余边界均为对称边界条件；墩柱为Z方向，水流为X方向，河床设置在X-Y平面上。

图1 模型建立示意图

3 冲刷深度计算方法评估

3.1 参数敏感性分析

在对各个预测公式进行评估前使用FLOW-3D有限元模拟得到不同参数变化下冲刷深度，探讨不同参数对冲刷深度的影响，寻找对冲刷深度影响较大或拥有某种规律的影响因素。各影响因素参考王诗泥等[27-28]以及工程实际情况进行取值，见表1。

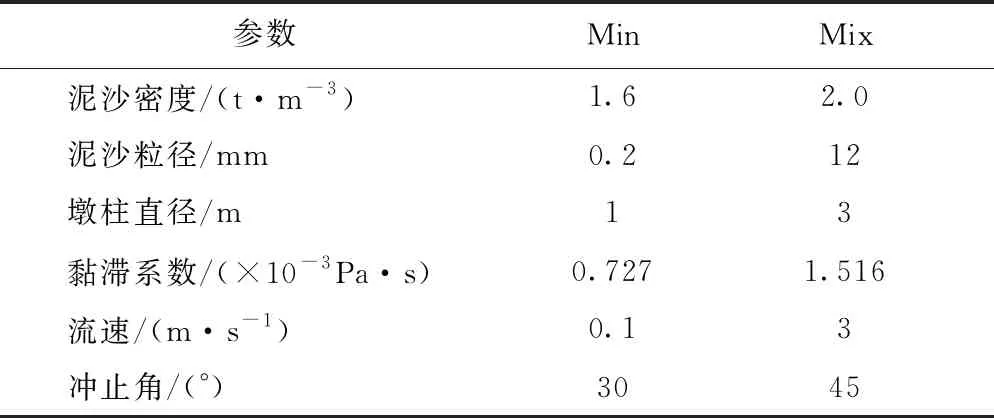
表1 各参数取值范围

从图2中可以得到：低流速状态下冲刷深度变化速率较快，但在超越低流速之后冲刷深度基本符合线性变化；冲刷深度随着泥沙密度的增大而减小，但是速率较小；冲刷深度随着墩柱直径的增加而增加，但其变化速率随着墩柱直径的增加而逐步减小，墩柱直径超越一定值后冲刷深度变化速率发展趋于稳定；泥沙冲止角在一定范围内对冲刷深度有所影响。泥沙密度、泥沙冲止角对冲刷深度的影响与流速、墩柱对冲刷深度的影响程度差异明显，改变冲刷深度的数量级不同。参考以上结果及工程实际需要，此次研究取流速和墩柱直径为主要影响因素，并进行适用范围分析。

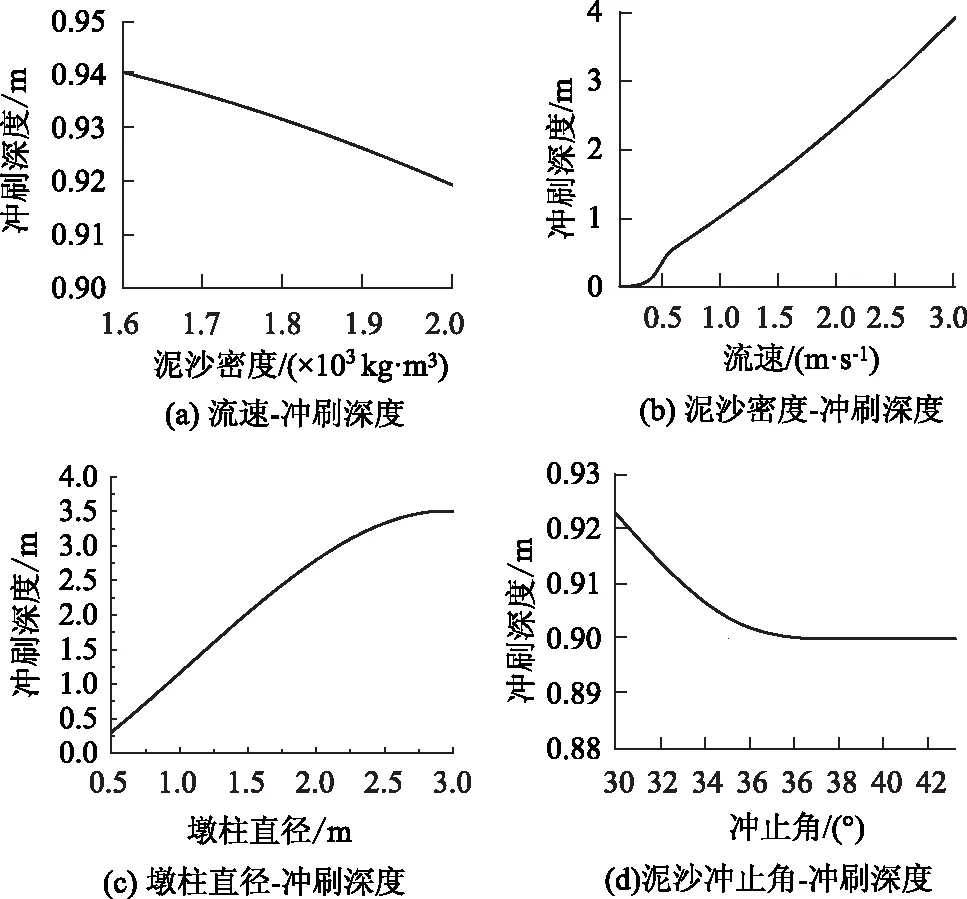
图2 不同参数对冲刷深度的影响

3.2 不同流速下冲刷深度的误差分析

这一部分的研究将在不同流速状态下使用各预测公式计算桥梁墩柱冲刷深度并使用FLOW-3D模拟相同情况下的冲刷深度，将两类数据进行对比并进行误差分析，对各预测公式进行评估。此研究将参考使用Mahmut Firat[29]的检验方法：

(12)

(13)

式中，DL为公式计算冲刷深度；DY为FLOW-3D模拟冲刷深度；n为数据总个数。CORR为相关系数，RMSE为均方根误差，CORR值越接近于1说明对比数据的变化规律越相似，RMSE值越小说明对比结果均方根误差越小。此检验方法不仅能够判断出各预测公式的计算结果与FLOW-3D模拟结果的变化规律相似性，还能够反映出各公式计算结果与FLOW-3D模拟结果的误差大小，以此来综合判断其相关性。

此节将使用不同的河床条件进行研究，现查阅长江水文网及李林林、夏军强等[30]对三峡水坝建成后长江下游河段的泥沙研究将河床进行分类，为初始河床和粗化河床两种类型，粒径信息见表3。

护理本科生的社会价值体现，社会地位要求，薪酬待遇和职称要求等，不是仅仅靠国家政策、学校改革、医疗体制改革等措施能够充分满足和不断完善，更重要的是，护理本科生要提高自身素质，提高专业知识和护理技能水平，提高护理科研水平，促进护理事业健康、长足发展。这样，护理本科生的社会价值自然会得到社会各界的认同，本科护生自身也会由内而外，提高对护理职业的认同感，从而热爱护理事业，为护理事业的蓬勃发展贡献力量。

表3 不同河床的粒径范围

针对两种不同的河床进行研究，墩柱直径取D=2 m；泥沙密度取1.8 t/m3；取20 ℃时水的黏滞系数；冲止角为45°。将FLOW-3D模拟结果与各公式计算结果绘图表示，进行不同范围的误差分析，以提高精度，结果如图3、图4所示。

图3 初始河床下冲刷深度随流速的变化图

图4 粗化河床下冲刷深度随流速的变化图

从图3与图4中可以得到：两种不同河床环境下各预测公式的计算结果差别明显；显然 Sung-Uk Choi法在两种河床环境下当流速超过了某一阈值后此方法所得冲刷深度基本趋于稳定；低流速时David J. McGovern法的计算结果与FLOW-3D模拟结果有一定的契合度，但当超过低流速后该方法计算结果与FLOW-3D模拟结果差异明显，并随流速增大而增大；其他计算方法均在低流速时与FLOW-3D模拟结果较接近，在流速变大过程中差异逐渐增大。

接下来使用式(12)和式(13)对获得的数据进行低流速和超越低流速的相关性分析，检验结果如表4和表5所示。

表4 低流速下冲刷深度误差分析

表5 超越低流速后的冲刷深度误差分析

从表4和表5中可以得到：在低流速、初始河床环境下Lanca法的计算结果CORR值最接近1，此时Lanca法与FLOW-3D模拟结果变化趋势最接近，但其RMSE值并不是最小，说明存在一定的误差；而Giuseppe Oliveto法此时的RMSE值最小，但其CORR值偏大，Cardoso法的CORR值与Lanca法的CORR值相差较小，并且此情况下Cardoso法的RMSE值也比较小。低流速、粗化河床环境下所有方法的CORR值相差不大，并且Reza法的RMSE值最小。超越低流速后、初始河床环境下所有计算方法的CORR值相差也不大，此时Giuseppe Oliveto法的RMSE值最小。在超越低流速后、粗化河床环境下Sung-Uk Choi法的CORR最接近于1，其他计算方法的CORR值偏大并且相接近，此时Sung-Uk Choi法的RMSE值很大，而Giuseppe Oliveto法的RMSE值非常小，此时Giuseppe Oliveto法的计算值与FLOW-3D的模拟值最接近，其计算误差最小。

3.3 不同墩柱直径下冲刷深度的误差分析

本节将对不同墩柱直径下各冲刷深度预测公式计算结果与FLOW-3D模拟结果的相关性进行探讨，此次研究同样将河床进行分类，将河床分为初始河床和粗化河床，泥沙粒径的取值同上节。本节的研究将流速取值为1 m/s，其他参数均与上一节相同，并使用式(12)和式(13)对计算结果进行相关性分析，探讨各预测公式计算结果与FLOW-3D模拟结果是否具有相似的变化规律，并对其误差进行分析。FLOW-3D模拟结果与各公式计算结果见图5及图6。

图5 初始河床下冲刷深度随墩柱直径的变化

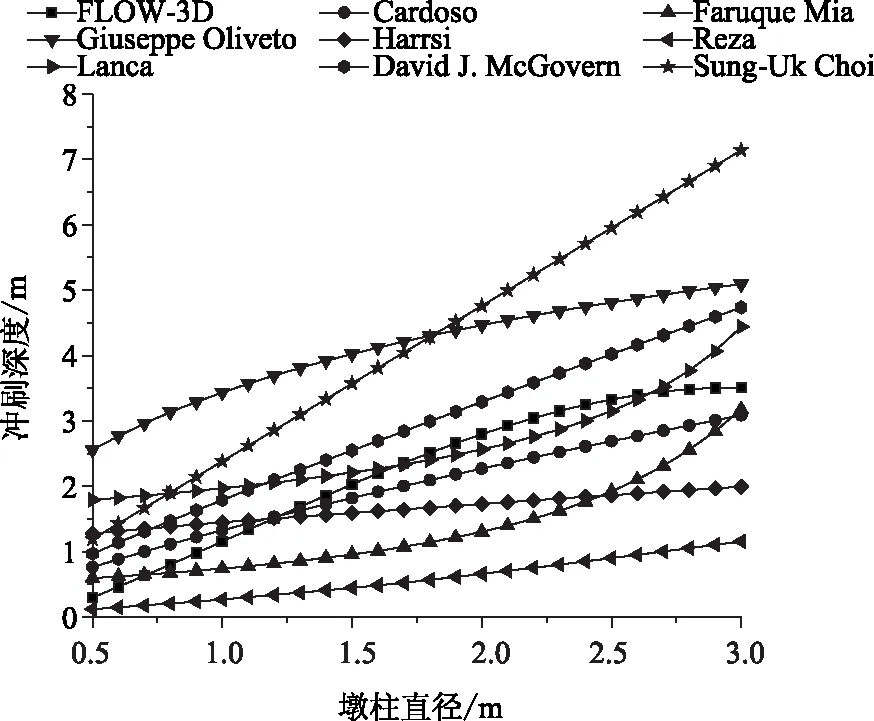
图6 粗化河床下冲刷深度随墩柱直径的变化图

从图5和图6可以得到：初始河床环境下流速较小时大多数预测公式计算结果均小于FLOW-3D模拟结果，并且随着流速的增大其差距愈发明显，此时Giuseppe Oliveto法、Sung-Uk Choi法与FLOW-3D模拟结果差异明显；而在粗化河床条件下各公式计算结果大致均匀分布在FLOW-3D模拟结果的两侧，此时各公式计算结果表现出了显著的变化差异。接下来使用式(12)和式(13)进行下一步的误差检验，检验结果如表6所示。

从表6可以得到：在初始河床环境下各公式的CORR值差异不明显，说明此时各公式的变化趋势基本一致，在某些区域有所差别；但此时各公式的的RMSE值相差较大，David J. McGovern法的RMSE值最大，说明David J. McGovern法计算值与FLOW-3D的模拟值有较大差异；而Cardoso法与Lanca法的RMSE差异很小并且是此时各公式RMSE中的较小值，说明此时Cardoso法与Lanca法的计算值与FLOW-3D的模拟值差异较小。在粗化河床的环境下各公式的CORR值差异也不明显，同时其RMSE值差异明显，此时Cardoso法、Lanca法与Harrsi法的差异不大，说明此时这3种方法的计算值与FLOE-3D的模拟值较吻合。

表6 墩柱直径变化下冲刷深度误差分析

整合以上信息后，可以得知，在不同情况下不同的冲刷深度预测公式计算结果与FLOW-3D的模拟结果相关性有显而易见的差异。对比分析后可以得到在何种情况下使用哪一种预测公式将得到较理想的结果：在低流速、初始河床环境下建议使用cardoso法对冲刷深度进行预测，这将得到变化规律、误差都较理想的数值；在低流速、粗化河床环境下建议使用Reza法预测冲刷深度；在超越低流速、初始河床环境或粗化河床环境下为尽可能地减小预测误差，建议使用Giuseppe Oliveto法，此时能得到较理想的冲刷深度预测值；在初始河床环境下考虑墩柱直径为重点因素时使用Cardoso法与Lanca法都将得到较理想的结果，而在粗化河床环境下考虑墩柱直径为重点因素时建议使用Cardoso法计算冲刷深度。如遇到环境情况重合并且影响因素重要性不明的情况，例如在初始河床考虑低流速与墩柱直径的情况下，使用Cardoso法和Giuseppe Oliveto法同时进行预测，取最大值。其他情况同样采取此方法。

4 基础合理埋置深度的研究

在实际工程中出现的水毁现象大部分是因冲刷引起基础埋置深度减小，基础埋置深度减小到某一值之后将导致墩柱无法满足原先的承载任务，墩柱将无法承受直至毁坏，所以如何合理地确定墩柱的埋置深度就显得格外重要。

前面的研究确定了不同预测公式的选用建议，这一节将根据研究给出的公式使用建议进行冲刷深度的计算，取最大值包络进行多项式拟合，将拟合后的各情况计算值作为墩柱的合理埋置深度。

前面的研究显示，墩柱直径和流速对冲刷深度的影响比其他因素更显著，并考虑到工程实际中有些因素的选用工作量较大，其工程实用性确定过程较复杂，更重要的是这些其他因素拥有一定的随机性，难以明确其具体效应，所以接下来的研究将墩柱直径和流速作为主要影响因素进行研究。

den=1.824+0.671V2.537+0.824D1.482，

(14)

式中den为拟合计算值，其他与前相同。

使用二维图分别显示流速、墩柱直径与冲刷深度的关系，如图7所示。

图7 计算结果与拟合结果示意图

图中拟合曲线的计算值均在公式计算值之上，将公式计算最大值进行了包络。此多项式反映了流速变化、墩柱直径变化对冲刷深度影响的基本规律。将此研究所得拟合计算值作为实际工程的基础合理埋置深度，此研究将为工程实际提供参考。

5 结论

通过对FLOW-3D计算数据与多公式计算数据相比较以及相关性检验对计算公式进行的评估，最后计算合理冲刷深度可以得出以下结论：

(1)流速与墩柱直径对冲刷深度的影响非常显著，流速与冲刷深度的关系趋于线性，墩柱直径与冲刷深度的比值随着墩柱直径的增大趋于定值。而泥沙密度与泥沙冲止角对冲刷深度的影响数量级较小，泥沙冲止角大于阈值之后对冲刷深度影响甚微，泥沙密度对冲刷深度的影响呈现出线性关系。

(2)低流速环境下各公式的计算值与FLOW-3D的模拟值都较为接近，但是超越低流速之后David J. McGovern法与Sung-Uk Choi法的计算值与FLOW-3D的模拟值有明显的差异。在一般墩柱直径环境下除Giuseppe Oliveto法其他各计算方法的计算值与FLOW-3D模拟值相接近，但是当墩柱直径不断增大之后Sung-Uk Choi法与墩柱直径的差越愈发明显。

(3)低流速环境下建议使用Cardoso法与Reza法进行计算取较大值作为此时的冲刷深度；在超越低流速之后建议使用Giuseppe Oliveto法；墩柱直径为主要变量时建议使用Cardoso法与Lanca法进行计算取较大值。如遇多变量同时变化时使用上述建议公式计算后取较大值。

(4)使用包络曲线进行拟合得到的基础埋置深度计算公式综合考虑了试验结果、有限元软件模拟结果和理论推导，能够提供更加合理的基础埋置深度，为工程实际提供参考。