基于EEMD-GRU的短期电力负荷预测方法
2022-04-20吕雪涛
李 涛,姚 婧,吕雪涛
(1.国网湖北省电力有限公司荆州供电公司,湖北 荆州 434000;2.武汉大学 计算机学院,湖北 武汉 430072)
近年来,由于经济发展和人口增长,全球电力消耗不断增加[1]。电力能源是影响地区社会经济发展的重要因素,对地区经济的改善作出了重大贡献。因此,推动经济发展离不开电力系统的建设与完善。短期电力负荷预测(STLF)是电力系统需求侧改革的一个重要方面,也是实现电力系统安全稳定运行的重要前提。
现有的短期负荷预测方法大致可分为传统统计和机器学习2类[2]。传统统计方法包括线性回归(LR)分析[3]、指数平滑[4]和自回归坐标移动正态分布(ARIMA)[5]。由于负荷数据存在许多固有的非线性特征,传统统计方法不能很好地学习这些非线性数据[6],无法满足STLF对负荷预测精度的要求。基于机器学习的预测方法包括模糊推理系统[7]、支持向量机(SVM)[8]和人工神经网络[9],都具有学习非线性特征的能力,其中反向传播神经网络(BPNN)与基于K-最近邻(K-NN)和K-means的多标签算法的组合模型在解决STLF方面能获得更好的表现。然而,BPNN 是一种前馈神经网络,不能很好地学习电力系统中的时序数据。为解决这一问题,研究者们将深度学习的方法应用到负荷预测领域,处理复杂的非线性模式。Shi等[10]提出了一种新的基于时间序列的深度递归神经网络(PDRNN),将一组用户的负荷分布批量输入到一个输入池中,使用聚合智能计量数据消除不确定性,通过增加数据多样性和数据量来解决过度拟合问题。但是,传统循环神经网络(RNN)由于时间深度过大,隐藏层简单,在进行误差反向传播时,会出现梯度消失的问题。针对此类问题,Hochreiter 等[11]提出了长短期记忆(LSTM)循环神经网络,通过门控制将短期记忆与长期记忆相结合,克服了传统 RNN 的不足。Kong等[12]提出了一种基于密度的聚类分析方法,采用LSTM捕捉负荷曲线中持续存在的微妙的时间消耗模式,大多数情况下能产生最佳预测。门控循环单元(GRU)是一种特殊类型的基于优化 LSTM 的循环神经网络,其内部单元类似于 LSTM,具有更强的收敛性。Jung等[13]提出了一种短期负荷预测模型,使用GRU更加关注关键变量,提升负荷预测精度。然而,电力系统中不仅有时序数据,还有时空矩阵、图像信息等高维数据,GRU 模型并不能很好地处理这些高维数据。卷积神经网络 (CNN)广泛应用于图像识别和预测领域,是处理高维数据的理想选择。陆继翔等[14]提出了一种结合门控循环单元和卷积神经网络的GRU-CNN混合神经网络模型,其GRU模块提取时间序列数据的特征向量,CNN模块提取高维数据的特征向量。
电网中的负载变化具有高度随机性和周期性,小样本数据的预测精度差。因此,提出一种基于集合经验模态分解(EEMD)和门控循环单元(GRU)的短期负荷预测方法(EEMD-GRU),以提高短期电力负荷预测的预测精度,实现电力系统安全稳定运行。
1 模型原理
1.1 集合经验模态分解(EEMD)
经验模态分解(EMD)是一种自适应信号时频处理方法,可以将原始复杂数据信号集自动分解为有限个固有模态函数(IMF),分解后的每个IMF信号分量代表原始信号中不同频率的特征信号,广泛应用于自适应时间序列数据信号分析模型[15]。如果原始信号的各种频率成分混合,EMD在进行信号处理时可能会出现模态混叠现象,致使固有模态函数无法有效分离。因此,为了避免模态混叠的发生,采用EEMD对信号进行处理。
为了反映原始信号的全部和局部特征,将高斯白噪声添加到原始信号中,找到原始时间序列的所有最大值和最小值点,使用三次样条插值函数拟合曲线,其中最大值点对应曲线的上包络线,最小值点对应下包络线。第1步,计算上下包络线的平均值m1;第2步,用给定原始信号X(t)减去m1,得到本征模函数f1,公式为:
X(t)-m1=f1
(1)
如果f1不满足固有模式功能的要求,则f1作原始信号,重复第1步和第2步得到f2,公式为:
f1-m2=f2
(2)
继续判断f2是否满足固有模式功能的要求,若满足作为结果输出,如果仍不满足,则执行下一次迭代。假设K次迭代,满足固有模态函数要求的第1个函数为:
fk+ 1=fk+mk+1
(3)
则,其余部分为:
X(t)-c1=R1(t)
(4)
通过多次加入高斯白噪声,最终得到的平均值即为EEMD分解后的负荷序列。
1.2 门控循环单元(GRU)
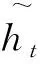
zt=σ(WZxt+UZht-1)
(5)
rt=σ(Wrxt+Urht-1)
(6)
(7)
(8)
式(5~8)中,WZ和UZ为更新门的权重;Wr和Ur为重置门的权重;W和U是形成防止内存的网络权重;σ为sigmoid函数。
2 EEMD-GRU预测模型
2.1 预测模型的建立
由于负荷数据具有高度复杂性、随机性和非平稳性,传统预测会受到很大的影响和限制。本文提出一种基于集合经验模态分解的门控循环单元(EEMD-GRU)预测模型进行电力负荷预测,EEMD- GRU模型如图1所示。该模型主要包括负荷数据预处理、EEMD-GRU模型预测和最终预测结果累加3个模块,具体过程如下。
1)对原始数据的缺省值和异常值进行预处理,剔除异常数据,将缺省数据用前后数据的均值代替,得到完整负荷数据。
2)利用EEMD对数据进行分解,将原始数据信号分解为有限个本征模函数(IMF)和残差分量,在每次分解中加入均匀分布的高斯白噪声,得到平均值并进行归一化处理。
3)GRU模型预测每个分量,依次得到每个分量的预测结果。
4)将每个分量的预测结果进行线性叠加,得到最终的预测结果。
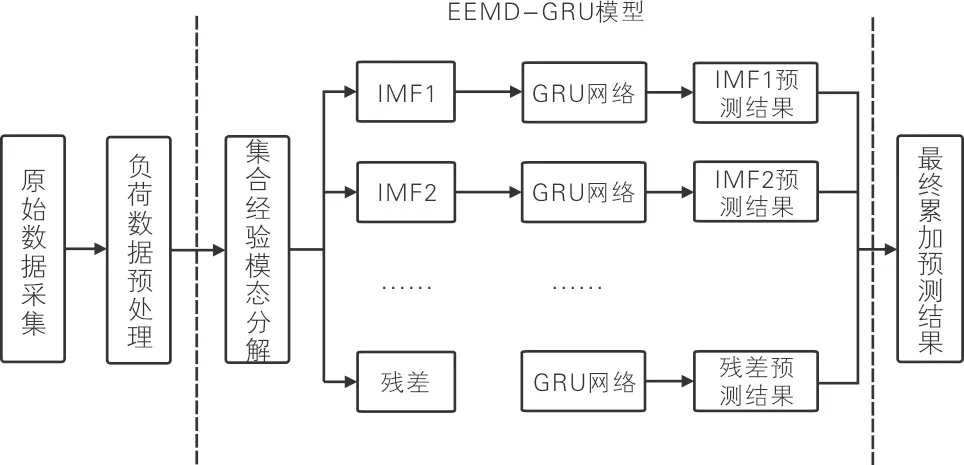
图1 EEMD-GRU模型
2.2 预测结果评价指标
为了评估预测模型的性能,引入平均绝对百分比误差(MAPE)和均方根误差(RMSE),MAPE和RMSE公式为:
(9)
(10)
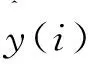
3 模型性能评估与算例分析
选取北美公用事业ISO-NE数据集(数据集的时间范围为2003年3月至2014年12月)和荆州电网实际数据为研究对象,将EEMD-GRU与GRU,LSTM进行比较,以MAPE和RMSE为评价指标,验证该模型的有效性。
3.1 测试用例1
在ISO-NE数据集中预测2003年3月至2004年3月的每日负荷数据。ISO-NE数据集每1 h采样1次,共8 760条数据。取前7 008条负荷数据作为训练集,剩下1 752条数据作为测试集进行模型评估。
1)由于原始数据的随机性、不确定性和非平稳性,在进行EEMD算法之前,需要对电网的负荷序列进行预处理。剔除一些异常数据点,提高预测的准确性,同时利用前后数据的平均值填充缺省数据。
2)采用EEMD方法对电力负荷曲线进行分解,在EMD的基础上加入均匀分布的高斯白噪声,将原始信号分解为10个IMF分量和1个残差分量。ISO-NE原始负荷数据及其EEMD分解的IMF分量和剩余残差分量如图2所示。

图2 ISO-NE原始负荷数据及其EEMD分解的IMF分量和剩余残差分量
图2中,IMF1~IMF6是序列频率分解后的较高部分,对应电网中较快的切换负载行为;IMF7~IMF10是序列频率分解后的较低部分,对应电网中较慢的开关负载行为;RES表示从原始信号中减去 IMF1~IMF10 分量后的剩余分量。
3)使用GRU模型进行分量预测。对原始分量数据进行最大最小归一化处理,设置GRU模型的参数时间步长为1,即从前一个负荷数据中预测下一个时间的数据。GRU 神经网络使用均方误差 (MSE) 作为损失函数,并在训练过程中通过自适应矩估计 (Adam) 算法优化 GRU 神经网络。对每个分量(IMFt+1,i,i=1,2,…,n)的预测结果及趋势项rt+1的预测值进行线性累加,得到最终预测结果。ISO-NE中IMF4和IMF7预测结果分别如图3和图4所示。

图3 IMF4预测结果

图4 IMF7预测结果
3.2 测试用例2
在荆州供电公司2020年7月31日至2021年3月19日共计232 d的实测负荷数据中,选择前218 d作为训练集,最后14 d作为测试集。按测试用例1的方法进行预处理和分量预测。荆州某台区原始负荷数据及其EEMD分解的IMF分量和剩余残差分量如图5所示。
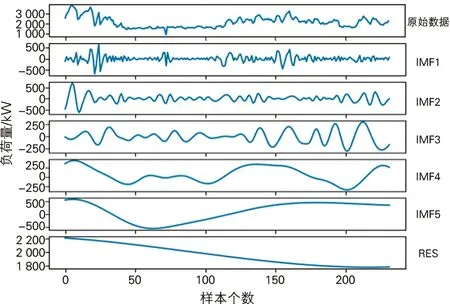
图5 荆州某台区的原始负荷数据及其EEMD分解的IMF分量和剩余残差分量
3.3 预测结果
采用平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为评价指标,将EEMD- GRU模型与LSTM,GRU模型进行比较。负荷预测结果见表1。
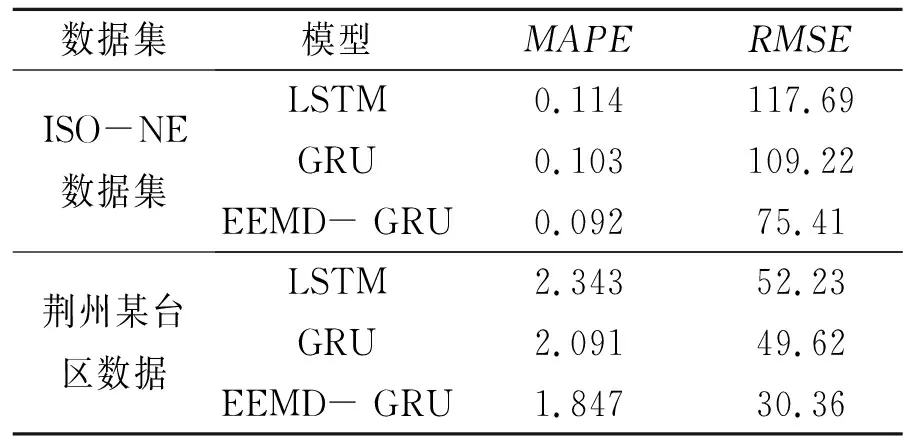
表1 负荷预测结果
由表1可以看出,EEMD- GRU模型与LSTM,GRU相比预测结果存在较大差距。与LSTM相比,在ISO-NE数据集上, EEMD -GRU模型的MAPE降低了23.91%,RMSE降低了56.07%;在荆州某台区数据上,MAPE降低了26.85%,RMSE降低了72.04%。与GRU相比,在ISO-NE数据集上,EEMD -GRU模型的MAPE降低了11.96%,RMSE降低了44.83%;在荆州某台区数据上,MAPE降低了13.21%,RMSE降低了63.44%,验证了EEMD -GRU模型的有效性和准确性。
4 结论
基于集合经验模态分解的GRU模型在原始信号中加入了高斯白噪声,将负载数据分解为有限个IMF和残差分量,有效避免了EMD可能存在的模态混叠问题,进一步降低了原始负荷序列的非平稳性。同时,利用RNN的改进模型GRU进行序列预测,不仅具有远距离历史信息记忆的能力,还具有超过LSTM的预测速度。通过在ISO-NE公开数据集和荆州电网实际数据上进行试验,验证了EEMD -GRU模型比GRU和LSTM模型具有更强的非线性拟合能力和更高的预测精度。
