扭曲乘积形式的2维双曲Yamabe方程①
2022-04-20胡玉琪赖晋秋姚纯青
胡玉琪,赖晋秋,姚纯青
西南大学 数学与统计学院, 重庆 400715
紧致黎曼流形上的Yamabe问题最早由文献[1]提出并证明, 但文献[1]的证明存在一定缺陷, 后由文献[2-3]进一步完善, 最后由文献[4]完全解决.
对于完备非紧致的流形, 文献[5]通过偏微分方程研究了预定曲率问题; 文献[6]研究了与双曲圆盘共形的完备度量的曲率; 文献[7]研究了圆盘上具有非正曲率的完备度量; 文献[8]研究了洛伦兹流形上的Yamabe问题; 文献[9]通过刘维尔方程给出了2维双曲Yamabe问题的一般解, 但解的形式比较复杂.
扭曲乘积度量是微分几何中研究黎曼流形和伪黎曼流形的一种重要的度量形式, 文献[10]利用Yamabe方程给出了扭曲乘积流形M×fN的数量曲率和两个因子流形M,N的数量曲率之间的关系; 文献[11]证明了在某些非紧乘积流形的共形类中, 无穷多个具有常数量曲率的完备度量的存在性; 文献[12]运用分叉定理和谱定理研究了扭曲乘积流形上Yamabe方程解的多重性.
1 预备知识

定义1如果乘积流形M=B×F上的度量g满足
g(X,Y)=gB(ρ*X,ρ*Y)+φ2(ρ(·))gF(η*X,η*Y)
其中X,Y是乘积流形上任意一对向量场, 则称g为扭曲乘积度量, 函数φ是B上正的光滑函数, 称为扭曲函数. 我们将此度量简记为g=gB+φ2gF, 将具有此度量的乘积流形称为扭曲乘积流形, 记为B×φF.
特别地, 当B是R+上的开区间I,F是Rn中标准单位球面Sn-1时, 扭曲乘积流形I×φSn-1上的度量
称为旋转对称度量.
设φ=snk(t)是方程组
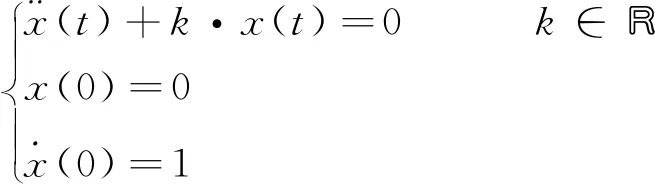
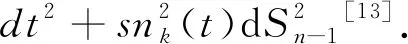
当k=0时,snk(t)=t, 流形R+×tSn-1与欧氏空间(Rn,ξ)等距, 其中ξ为标准欧氏度量.
当k=1时,snk(t)=sint, 考虑映射


可以验证G是一个等距映射, 因此流形R+×sintSn-1与标准单位球面(Sn,h)等距, 其中h是球面Sn上的标准度量[13].
当k=-1时,snk(t)=sinht, 可以证明流形R+×sinhtSn-1与双曲空间(Hn,h1)等距, 其中h1为双曲空间上的标准度量(引理1).
流形(Mn,g) 上的拉普拉斯算子定义为
Δ=δg∘d=-tr(∘d)
对任意的函数f∈C∞(M), 在局部坐标图下, 有
(1)
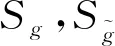
(2)
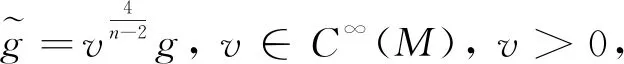
(3)
取球面上的北极点N(0, …, 0, 1) 为投影中心, 通过球极投影

球面上标准度量h表示为[14]
设φ是(Sn,h)到它自身的共形微分同胚, 则ψ=π∘φ∘π-1是(Rn,ξ)上的共形微分同胚, 从而可写为
ψ=A∘B∘C
其中A∈O(n),B是平移变换, 记B(x)=π(x)+a,C是伸缩变换, 记C(x)=λπ(x),λ≠0. 通过计算可得
因此得球面上的共形变换[3]
(4)
我们知道, 标准双曲空间(Hn,can)有3个常用的模型, 分别为双曲面模型(Hn,h1)、 庞加莱球模型(Bn,h2)和庞加莱半空间模型(Un,h3). 取Rn+1中双叶双曲面下半支的顶点S(0, …, 0, -1)为投影中心, 通过双曲球极投影

双曲空间Hn上的度量h1表示为[14]
2 主要结果
取(Hn,h1)作为我们所用的模型, 它是在坐标(τ,ξ1, …,ξn)中由方程τ2-|ξ|2=1定义的Rn+1中的双叶双曲面的上半支, 具有度量
h1=ι*m

引理1映射


是一个等距映射.

z1dz1+z2dz2+…+zndzn=0
从而
引理1得证.
下面我们要写出扭曲乘积流形上的Yamabe方程, 为此, 先给出扭曲乘积形式下的拉普拉斯算子.
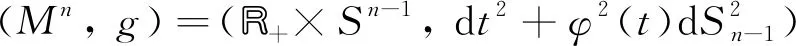
(5)
证首先, 黎曼度量g在局部坐标图下可表示为
其中
(gt)ij=φ2(t)hiji,j=2,…,n
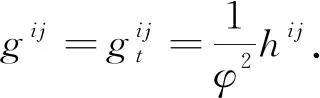
再由
可得
因为∂iφ=0, 则
整理即得
引理2得证.
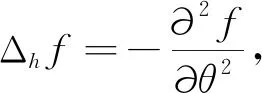
(6)
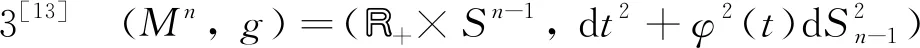
(7)
根据(2),(6),(7)式, 扭曲乘积流形R+×φS1上的Yamabe方程可写为
(8)
其中μ为常数.

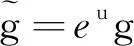
我们知道, (R2,ξ)上的共形变换即为相似变换, 共形因子为常值函数, 而常值函数恰好是我们所给方程的一组解.
当k=1时, 扭曲乘积流形R+×sintS1是与标准单位球面S2等距的.
定理1扭曲乘积流形R+×sintS1上的Yamabe方程为
该方程在μ=2时具有如下形式的解:
其中λ∈R+,a∈R2,z∈S1.
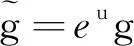
考虑等距映射


令z=(cosθ, sinθ)表示单位圆周S1上的任意一点. 那么x=(sintcosθ, sintsinθ, cost)表示S2上的任意一点, 由(4)式可得共形因子
eu=4λ2[1+λ2+|a|2-(1-λ2+|a|2)cost+2λsint(a1cosθ+a2sinθ)]-2
即
它是我们所给的Yamabe方程的解, 定理1得证.

定理2扭曲乘积流形R+×sinhtS1上的Yamabe方程为
该方程在μ=-2时具有如下形式的解:
其中λ∈R+,a∈R2,λ2+|a|2<1,z∈S1.
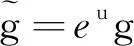
仿照标准单位球面上的共形变换(4), 我们构造双曲空间上的共形变换为
(9)
考虑等距映射


令z=(cosθ, sinθ)表示单位圆周S1上的任意一点. 那么x=(sinhtcosθ, sinhtsinθ, cosht)表示H2上的任意一点, 由(9)式可得共形因子
eu=4λ2[1+λ2-|a|2+(1-λ2-|a|2)cosht-2λsinht(a1cosθ+a2sinθ)]-2
即
可以验证它是我们所给方程的一组解, 定理2得证.
我们利用扭曲乘积流形研究了2维双曲Yamabe方程及其特解, 但要推广到更高维的双曲空间, 甚至更一般的扭曲乘积流形还需要进一步地开展研究.
