中小学课堂教学质量的模糊多级评价模型

任延青， 鱼先锋

(1.商丹高新学校，陕西，商洛 726000;2.商洛学院,数学与计算机应用学院, 陕西，商洛 726000)

0 引言

中小学教学质量评价是师生教学的指挥棒，它直接决定师生教学行为。科学的教学质量评价可以充分调动师生的积极性，促进学生全面协调发展和教师教学水平提高,也可作为教师考核的重要依据。近年来，无论在理论还是实践上，对课堂教学质量评价都有了较大的进展。2002年教育部《关于积极推进中小学评价与考试制度改革的通知》和《基础教育课程改革纲要(试行)》是学生综合素质评价的直接的政策依据[1]。2013年6月，教育部出台《关于推进中小学教育质量综合评价改革的意见》，规定包括学生品德发展水平、学业发展水平、身心发展水平、兴趣特长养成、学业负担状况等五大方面20项关键指标的中小学综合素质评价内容，并明确了评价的程序[2]。2014年9月3日国务院《关于深化考试招生制度改革的实施意见》明确了综合素质评价与考试招生制度实行“硬挂钩”。从上述政策的发布可见，我国对中小学生综合素质评价的目的和定位由不明确变明确[3]。教学质量评价始终是学生综合素质评价的核心内容之一。评价方法是评价体系的重要组成部分，在评价实施过程中扮演着重要的角色。如果说理念是评价的灵魂，决定着评价的性质和取向，那么技术和方法就是评价的骨骼，支撑和架构起评价的各相关因素，决定着评价完成的质量[4]。所以近年来很多教师和学者在中小学课堂教学评价方面进行了大量的研究工作[5-8]。但是,这些研究多重于定性分析缺少定量计算，多偏于手工评价没有给出自动化实现模型与方法。现实评价中既有定性信息也有定量信息，人工评价费时费力且容易出错。模糊评价可以有效地综合定性与定量信息对评价对象进行更自然、客观的描述和评价[9-12]。作者在充分研习国家教育方针政策、教育评测标准的基础上，结合自身多年从教经验，设计了中小学课堂教学评价指标体系，基于模糊计算基本理论建立了中小学课堂教学质量的模糊多级评价模型，结合定性与定量信息，自然、客观地对课堂教学质量进行评价。结合实例做了课堂教学质量评价，结果显示该模型客观、高效且自动化程度高。

1 形式化评价模型

先给出模糊综合评价的一些基本概念包括模糊集、模糊评价矩阵、权重、评价算子等。在此基础上对模糊多级评价形式化建模给出一个普适的评价模型。

1.1 模糊评价的理论准备

定义1[13]设X为经典集合，称映射，A:X→[0,1]为X上的模糊集(Fuzzy set)，∀x∈X，A(x)称为x对A的隶属度，函数A也称为模糊集A的隶属函数。

在模糊评价过程中X是评价指标之集，A是评价等级，∀x∈X，A(x)是指标x隶属于评价等级A的可能性测度。隶属度在[0,1]上取值，取值越大表明隶属可能越大，即∀x1,x2∈X，A(x1)≤A(x2)表示指标x1对评价等级A的隶属程度不超过指标x2。一般地，隶属度函数刻画了评价对象对评价等级隶属程度和隶属程度相对大小2个属性信息。

定义2 在一次模糊评价中，有m个评价指标，n个评价等级，则模糊评价矩阵为

(1)

其中，∀rij，rij∈[0,1]表示第i个评价指标对第j个评价等级的隶属度。初级评价矩阵一般由原始评价数据模糊化得到。原始评价数据为

(2)

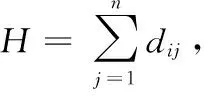
权重可以通过特尔斐法、层次分析法、二项系数法、变异系数法、主成分分析法等方法获得[14]。

定义4 在一次模糊评价中，有m个评价指标n个评价等级，则模糊评价矩阵为

(3)

各指标对应权重之集为W=(w1,w2,…,wm)，记E′∈[0,1]m为此次评价结果，定义评价算子“*”如下。

(1)乐观评价算子(max-product)，

(4)

(2)悲观评价算子(min-product)，

(5)

(3)综合评价算子(sum-product)，

(6)

命题1 乐观模糊评价算子(max-product)刻画评价对象对每个评价等级最大隶属程度，体现了最大隶属原则；悲观观模糊评价算子(min-product)反映评价对象对每个评价等级最小隶属程度，是一种保守考虑；综合评价算子(sum-product)体现了评价的期望结果，符合概率统计规律。

没有采用模糊计算理论的经典模糊合成算子max-min运算, 有两方面考虑。首先，max-min运算已被证明将权重(wi)和评价值(rij)取小的结果不合理[15]，因为wi∧rij只是单方面权重wi或此级评价值rij,不能客观反映出高一级评价结果。其次，权重wi较小时，对应评价值rij的信息会被淹没。权重与评价值的乘积(product)才体现了乘法原理和统计学基本规律。

1.2 形式化模型

下面对模糊多级评价模型进行形式化建模。约定k表示评价等级数。g1,g2,…,gk∈N+,gi表示第i层每个指标的指标个数。

max{g1,g2,…,gk}=n为各层指标个数最大值。∀k∈N+,定义I(k)={1,2,…,k}则，

im∈I(gm),j∈I(n),m∈I(k)

(7)

序列i1,i2,…,ik∈N+k,gi标识第im个m级指标的位置。i1，i2，…,ikj∈N+k,gi标识第im个m级指标的第j个等级的测度(样本分布数、隶属度)的位置。用序列#gi,…,gk∈N+ω,标记k,k-1,…,i+1层评价已经做完正要做第i层评价。

定义5 一个模糊多级评价模型(Fuzzy Multilevel Evaluation Model,FMEM)E是一个六元组,E=(AP,R,D,W,δ,S)，其中记号意义说明如下。

(1)AP={λ1,λ2,…,λn}表示评价等级之集，∀λi∈AP是结构体数据，封装了第i个评价等级的标识及其对应的特征区间或特征值。特征区间和特征值一般取百分制区间和百分制实数，是去模糊化时对各等级打分要用的数据。

(2)原始数据矩阵D存储记录初级指标的初始评价值，D=Dg1g2…gkn是一个k+1维的矩阵，∀di1i2…ikj∈Dg1g2…gkn表示第im个m级指标在第j个等级λj的样本分布个数。

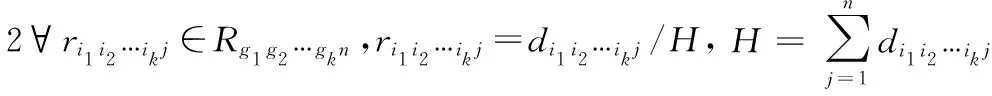
(4)权重矩阵W存储记录初级指标的初始评价值，W=Wg1g2…gk是一个k维的矩阵，∀wi1i2…ik∈Wg1g2…gk表示第im个m级指标在m层评价时的权重。

(5)映射δ:W×R→R是模糊评价函数，根据定义4关于模糊评价算子的定义有，

(8)

(6)得分矩阵S存储记录每一级指标评价得分，S=Sg1g2…gk是一个k维的矩阵，则，∀s#imgi+1…gk∈Sg1g2…gk，表示第im个m级指标的得分。则有

(9)

其中,r#(imj)gm+1…gk表示第im个m级指标对第j个等级的隶属度，λj表示第j个等级的特征值。一般我们只计算一级评价的最终得分，其他等级不做计算。

定理1E=(AP,R,D,W,δ,S)为FMEM,若需要k级评价，每一级指标个数不超过m，每个指标的评价等级分n级，则做k级模糊多级评价的时间和空间复杂度都为o(mkn)。

定理1指出FMEM的复杂度随评价等级数k呈指数增长，但现实中评价等级数一般较小，常见的k∈I(5)。所以FMEM是易于在计算机上实现的。

2 评价实例

下面以中小学课堂教学评价为例，对FMEM进行应用。

2.1 中小学课堂教学评价指标、权重的建立

量化评价的核心是指标体系的建立和权重的确定。在充分研习国家教育方针政策、教育评测标准的基础上，结合自身多年从教经验，设计了中小学课堂教学评价指标体系如表1所示。表中第1列给出了“教学目标”“教学内容”“课堂结构”“教学方法”“教学效果”“教学基本功”等6个一级评价指标，第2列对每个一级指标细分共给出了“符合大纲、教材要求”等23个二级指标，并根据特尔菲法确定了每个指标的权重。

表2截取了表1中部分，其中第2个一级指标“教学内容R2”对应的第2个二级指标“难易适度，容量适当R22”，R223=1是没有模糊化之前指标R22分布在等级λ3=“及格”的样本数，其模糊化后实际存储为0.1。w22=20%=0.2表示第2个一级指标“教学内容R2”对应的第2个二级指标“难易适度，容量适当R22”在二级评价时所占权重为0.2。

表2 R存储记录各级指标与评价值示例

2.2 数据获取与评价

作者将表1中的23个二级指标列到表上，在学校期中教学检查集体听课时发给11名听课教师，对作者所带某门课程进行评价。听课教师只需要在各指标对应等级“优秀、良好、中等、及格、差”下打“√”即可。收回10张打分表，统计结果为表1中最后5列所示各指标对应不同等级选择人数。

表1 指标体系与原始评价数据

对应于定义5给出的FMEM模型对模型参数初始化，并用模型进行课堂教学质量的模糊多级评价。样本数H=10，评价等级数k=2，评价等级划分在表3中给出，

表3 各评价等级的特征值

AP={λ1,λ2,…,λ5}=

(优秀/95，良好/85，一般/75，及格/65，差/50)

(10)

(12)

(14)

类似地可计算得到

(15)

依据定义5的(6)计算最终得分计算一级指标评价得分为

(16)

类似算得，

S2=90.10,S3=87.20,S4=85.50,S5=83.44,S6=87.00

(17)

S2∈[90,100]=λ1说明该教师在所评价课堂上第2个一级指标“教学内容”评价为“优秀”；S1,S3,S4,S5,S6∈[80,90)=λ2说明该教师在所评价课堂上除了第2个一级指标外其余5个一级指标评价均为“良好”。

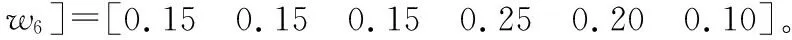
一级评价计算如，

sum(E′)=1,所以,

(19)

依据定义5的(6)计算最终得分,

(20)

因为84.96∈λ2=[80,90)，所以对该教师这堂课的评价结果是“良好”。

3 总结

设计了中小学课堂教学评价指标体系(表1)。定义了3个模糊评价算子(定义4)，讨论了评价算子的合理性(命题1)。基于模糊计算基本理论建立了中小学课堂教学质量的模糊多级评价模型(定义5)，结合定性与定量信息，自然、客观地对课堂教学质量进行评价。讨论了用FMEM进行模糊多级评价的复杂度，证明了该模型高效且自动化程度高(定理1)。结合实例进行了课堂教学质量评价，结果显示所评价教师本节课教学质量“良好”。

后续工作考虑：①模型加上时间维度，考虑被评价对象在时间变化上教学质量的变化，以发展的眼光看待被评价对象；②课堂评价打分不限于同行教师，可考虑领导、学生打分，进行3级综合评价；③将FMEM应用与其他背景，比如水质评估、旅游景点满意度评估、矿井安全评估等。