过程性作业——让学习真正发生

汪 琼

（浙江省杭州市富阳区职业高级中学，浙江 杭州 311400）

一、什么是过程性作业

过程性作业是教师根据教材和学情设计，提供给学生自主学习，提高数学素养的一种学案。学生依托过程性作业，在教师引领、同伴互助下进行深度学习，体验成功的快乐，获得持续性发展。

二、过程性作业的设计理念

1.体现过程，优化体验

学习通常要经历观察、假设、推理、计算、验证、归纳等过程，过程性作业必须要体现出上述过程，让学生建构起作业承载的知识体系。学生在深度学习的过程中，提高了合作能力、自主探究品质，学会了反思，获得了解决问题的成就感。

2.富有层次，循序渐进

过程性作业是学生自我学习的媒介，因此，教师在设计作业时应当遵循问题或内容由浅入深，由易到难的原则。学生在循序渐进地解决问题，完成任务过程中达到自我学习，自我成长的目的。

3.形式多变，激发兴趣

过程性作业不能变成一种学生的简单习题，应该形式多样化：如动手操作做学具、画单元思维导图、观看微视频完成预习作业、错题整理、当小老师编题等。这些灵活多变的过程性作业，能大大激发学生的学习兴趣。

三、过程性作业的内容开发

1.预习式作业

高一《一元二次不等式》这节内容，是初中到高中知识难度跨越很大的一节，需要联系学生初中学习的一元二次方程，一元二次函数内容。为了帮助学生顺利过渡，笔者设计了一份预习式作业。

案例1

《一元二次不等式》预习作业

含有一个未知数，并且未知数的最高次数为二次的不等式，叫作一元二次不等式，标准形式如：

ax2+bx+c＞0（≥0），ax2+bx+c＜（≤0）（a≠0）

一．解下列一元二次方程。

x2-x-6=0 x2-6x+9=0

二．已知一元二次函数y=x2-x-6，

1.画出这个二次函数的草图（草图体现开口方向，与x轴交点即可）。

2.抛物线与x轴的交点是______________，其交点将x轴分成________段。

3.（1）当y=0即x2-x-6=0时，自变量x的取值是______。

（2）当y＞0即x2-x-6＞0时，函数对应图像位于____，此时自变量x的范围是______，x2-x-6＞0的解集为______。

（3）当y<0即x2-x-6＜0时，函数对应图像位于______，此时自变量x的范围是______，x2-x-6＜0的解集为______。

学生自主完成预习作业，把初中的解一元二次方程，一元二次函数的知识联系起来。通过动手画图像、观察图像、动脑思考，初步了解图像法解一元二次不等式的方法。学生完成预习作业后，再听教师讲解新课，更容易理解新课内容。一份简单的预习式作业引导学生独立思考，自主探究，往往能帮助教师突破难点，强化重点，达到事半功倍的效果。

2.反思式作业

学生要学好《二项式定理》这节内容，需要较强的计算能力。在练习过程中，一些典型习题学生往往屡做屡错。对于运算类习题课，教师如果单单采用讲练结合的形式，学生觉得枯燥乏味，教学往往收效甚微。基于此，笔者设计了一份反思式作业，帮助学生突破计算瓶颈。

案例2

《二项式定理》错题反思作业（部分）

【我是华佗】

病因分析：

对症下药：

【滋补佳品】

学生通过完成反思式作业，分析错误原因，所用到的算理或知识点，在理解的基础上完成矫正练习。学生在“反思”——“理解”——“矫正”的深度学习过程中，达到了举一反三，融会贯通的效果。教师也破解了“教不会”的困惑，小小的“反思作业”起到了一两拨千斤作用。

3.思维导图式作业

立体几何模块定理和性质多，学生如果对定理和性质不熟悉，碰到题目往往不知如何下手。为了学生能深入地理解这些定理和性质之间的关系，笔者设计了一份思维导图式作业。

案例3

《空间的平行和垂直》思维导图式作业

请同学们根据图示归纳定理或性质，仿照例子写出命题文字语言，符号语言并画图。

1.线面、面面平行的定理和性质

2.线面、面面垂直的定理和性质

图形：

文字语言：如果平面外一条直线平行于平面内一条直线，那么这条直线就与平面平行。

学生对照书本找每一个“箭头”对应的定理和性质，画图，厘清线面关系。在完成作业的深度学习中，将平行、垂直关系系统化，在脑海中织就一张关系网；又像“庖丁解牛”一样细节化，分解出每一个命题中条件与结论之间的关系。在碰到判断命题真假，证明线面平行或垂直类型的题中，马上能找到解题切入点。教师制作“思维导图式”作业，在复习课中能引导学生把整章内容牵线搭桥式的进行整理。

4.编题式作业

上完《数列》这一章后，学生感觉这部分内容公式很多，错综复杂。等差数列，等比数列都涉及首项、末项、中项、前n项和、通项之间的关系。为了让学生灵活运用数列公式、性质，笔者设计了一份编题式作业。

案例4：

《数列编题式作业》

在《等差数列》中，我们学习了下列公式，

请你当一次小老师，根据下列条件编题并解答：

要求：已知等差数列 a1,n,d, an,Sn中的任意三个量，求剩下的两个量。

编题1：____________________________________.

解答：

编题2：____________________________________.

解答：

在《排列组合》这章内容中，学生总是分不清哪些题是排列问题，哪些题是组合问题。为了激发学生的兴趣，理解排列问题和组合问题的区别，笔者设计了一份编题式作业。

案例5

《排列组合编题式作业》

你知道如何区分排列问题和组合问题吗？如果选出的元素在安排时有序，就是排列问题，无序就是组合问题。检验是否“有序”，可以变换某一结果中两元素的位置，结果有变化就是“有序”。

例：从高一（2）班的30位同学中选2位做班干部，是组合问题。

从高一（2）班40位同学中选2位分别担任班长和纪律委员，是排列问题。

请你结合生活实际，再编2道组合问题和排列问题的题目。

组合问题：1.____________________________________

2.____________________________________

排列问题：1._____________________________________

2.____________________________________

把你编的题目拿给身边的同学做一做吧！

“编题式作业”，化学生被动解题为主动编题。学生把自己编的题目再拿给身边的同学做一做，在探究过程中，启迪思维，相互促进，教学难题迎刃而解。

5.实践操作式作业

在立体几何《多面体和旋转体》内容中，已知圆锥底面半径，母线长，求圆锥的侧面积，体积是常常出现的题目。圆锥的侧面展开图是扇形，求侧面积和体积时还与扇形的圆心角等相关，比较复杂。为了让学生将公式熟记于心并灵活应用，培养学生的动手操作能力，笔者设计了一份实践操作式作业。

案例6

《圆锥的侧面积和体积》操作式作业

一．画一画，剪一剪

请你在白纸上确定圆心和半径，用圆规画一个扇形，并剪下这个扇形。建议圆心角取特殊角，如30度，45度，60度，120度，135度，150度中任选一个。

二．量一量，记一记

测量扇形的半径和圆心角，并在本子上做好记录。

三．做一做，算一算

把剪好的扇形围成一个圆锥，根据记录的数据计算这个圆锥的侧面积和体积。

（1）扇形半径：______cm 扇形圆心角：______

求圆锥的侧面积和体积

在《椭圆的定义与标准方程》一节中，为了让学生实际体验椭圆的形成过程，会求椭圆的长轴，短轴，焦距等，笔者设计了一份实践操作式作业。

案例7：

《椭圆的定义与标准方程》实践操作作业

你能画一个标准的椭圆吗？

材料准备：

一条长度一定的线绳，两枚钉子，一支铅笔，两块画板（可以在木板上贴上白纸）。

二．操作步骤

（1）画板横放，将绳子的两端用钉子固定在画板上的F1和F2两点，并使绳长大于F1和F2之间的距离。

（2）用铅笔尖将线绳拉紧，并保持线绳的拉紧状态，笔尖在画板上慢慢移动，画一个椭圆。

问题：M点在移动过程中，MF1与MF2的距离之和变化吗？如果不变，MF1与MF2距离之和就是什么？

____________________________________

（3）你会通过建立平面直角坐标系，得到椭圆标准方程，求出长短轴的长度，焦点坐标吗？

在第一块画板（横放）上，以两个钉子所在直线为x轴，以F1F2的中垂线为 y轴，建立直角坐标系（用铅笔画图）。测量F1F2间距离，绳子的长度（接头处不计）

根 据|F1F2|=2c，|MF1|+|MF2|=2a得 测 量 的 结 果：a=______，c=______。根据a2=b2+c2得b2=______。根据焦点在x轴上的椭圆标准方程：，你画得椭圆标准方程是：____，焦点坐标____，长轴长____，短轴长____。

（4）在第二块画板（竖放）上，重复一、二步骤。

根 据|F1F2|=2c，|MF1|+|MF2|=2a得 测 量 的 结 果：a=______，c=______。根据a2=b2+c2得b2=______。根据焦点在x轴上的椭圆标准方程：，你画得椭圆标准方程是：____，焦点坐标____，长轴长____，短轴长______。

实践操作式作业体现了“做中学”的教育思想，教师引导学生根据主题任务，通过观察、操作、类比、归纳等具体活动，自主探究圆锥的侧面积和体积的求法、椭圆的形成过程及椭圆的标准方程。学生在过程性的深度学习中，提升了动手操作能力，数形结合能力。

6.总结式作业

为了让学生对《正、余弦定理与解三角形》这一节内容定理、公式、题型进行归纳总结，会根据不同条件选择适当的定理解题，笔者设计了一份总结式作业。

案例8

《正、余弦定理与解三角形》总结式作业

【理一理】在《正、余弦定理与解三角形》中，我们学过了正余弦定理和三角形面积公式，还知道了根据不同已知条件选择合适的定理解题。请你用思维导图、框图或树状图的形式进行归纳。

【找一找】根据不同的已知条件，我们要学会选择合适的定理解题，请你结合自己上面的总结，按照下面的例子，列举几种不同的题型。

例：

题型：已知两角对边，选择正弦定理求另一角的对边。

解答：

题型一：______________________________

例题1：_________________________________________

解答：

【纠一纠】本节内容有哪些易错题，向同学们推荐几题。

（1）题目______________________________________，

易错点：______________________________________。

（2）题目：_____________________________________，

易错点：______________________________________。

教师在章节复习中引导学生用框图、思维导图、树形图等形式对概念、定理、公式、性质等基础知识进行梳理归纳，理清知识点。学生在完成过程性作业中，构建起知识网络，查漏补缺。题型归纳和错题自纠，帮助学生深度思考，自我学习。这样的复习方式，比老师总结，学生被动接受更有实效性。

7.专业结合式作业

电子电工中的正弦交流电与数学中的正弦型函数联系紧密。专业课老师向笔者反应，学生相关知识的数学基础不够。为了让学生会求正弦交流电的三要素：振幅、周期、初相位。会求正弦交流电的有效值，相位差。笔者设计了一份专业结合式作业。

案例9

一．学一学

在数学中，我们把形如 y=A sin(ϖx +ϕ)的函数叫作正弦型函数。其中A叫做振幅，ω叫作角频率，ϕ叫作初相。

在电工专业中，常用 i=Imsin( w t+ϕi0)和e=Emsin(ϖ t +ϕe0)来表示交流电中电流和电压的瞬时值。其中，i，e，u为电流，电动势，电压的瞬时值；Im，Em，Um为电流，电动势和电压的最大值；ω为角频率，ϕ0为初相位。

（1）周期

完成一次周期性变化所用的时间叫作周期。用T表示，单位是秒。

（2）频率

交流电在单位时间内完成周期性变化的次数，叫作频率。用f表示，单位是赫兹。

（3）角频率

在e=Emsin(ϖ t +ϕe0)中，ϖ是线圈转动的角频率。角频率和周期、频率有如下关系。

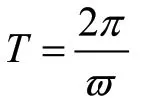
（4）初相位和相位差

当t=0时，相位ϕ0叫作初相位。

二．练一练：

通过这份专业结合式作业，学生学会将正弦型函数与正弦交流电结合，应用数学知识解决专业问题。

四.关于过程性作业开发的思考

1.源于教材，整合开发

教材中有一些实践操作内容，教师可对其进行加工，设计以现实问题为背景的过程性作业，使学生体会到数学的实用性。

2.学科互通，多元开发

教师还可结合各学科中的数学知识开发过程性作业，如建筑和机械专业相关知识结合二面角等。这种跨学科的作业能大大激发学生的兴趣，不仅强化了数学知识，还巩固了专业知识，体现了数学学科的工具作用。

3、不同层次，各有发展

过程性作业，因为设计中体现了学生自我反思，自我总结，自我创造的思想，从而促进学生深度学习，使不同层次的学生数学素养都得到发展。

教师开发多样化的过程性作业，改变了传统作业的单一性，灵活多变的形式让学习不再枯燥。学生在深度学习中，优化了认知结构，形成了学习方法，积累了活动经验。过程性作业，让学习在学生身上发生，真正实现了“授之以渔”。