轴向磁通永磁同步电机气隙磁场解析计算

李柘霖，于慎波，夏鹏澎，于言明

(1.沈阳工业大学 机械工程学院,沈阳 110870；2.中国邮政集团公司辽宁省机要通信局,沈阳 110000)

0 引 言

近年来，随着永磁体材料性能的提高，永磁同步电机也在快速地发展。轴向永磁电机(Axial Flux Permanent Magnet Motor，AFPMM)也称盘式永磁电机，因其结构紧凑、工作效率高、功率密度大等特

性而得到越来越多的关注。AFPMM更多的应用在电动车辆、可再生能源系统、飞轮储能系统和工业设备等要求高转矩密度和空间紧凑的场合[1]。盘式电机具有多种拓扑结构，不同结构形式、应用场景及其性能也各不相同[2]。其中为了克服单边磁拉力问题，中间转子或定子的双边结构是应用最为广泛的盘式电机结构。该结构形成双气隙，电机转子不仅可以保持动态平衡，而且有益于提高功率，更便于散热，因此性能较优越、功率密度较高[2]。但是由于盘式电机磁路结构的特殊性，决定了其在计算磁通密度、振动噪声等性能参数时，较多采用3D有限元仿真来计算[3]。有限元仿真分析计算速度慢，建模复杂，占用计算机资源较大，对电机优化进程产生严重影响。为了解决仿真分析的局限性，国内外学者进行了研究，提出了一些解析法，取得了一定成果。

对于轴向磁通永磁同步电机的解析分析法大多学者采用将盘式电机3D模型等效成多个2D直线电机模型，以缩短计算时间[4-6]。文献[7]通过运用许-克变换法，求解与不开槽结构相比齿槽结构对应的气隙相对磁导函数来考虑齿槽效应，验证了电机在槽口宽与槽节距比值较小时可忽略相邻槽之间的影响。但没有计算负载情况下的气隙磁场。文献[8]把轴向磁通磁场调制型电机沿平均半径处展开并且忽略定子开槽影响，建立了二维解析模型，来求解轴向气隙磁场。在文献[9-10]中将遗传算法与有限元分析法相比，此方法在设计之初，解析解更可取。在文献[11-13]中，均采用了子域法来分析求解麦克斯韦方程进而求出气隙磁通分量。文献[14]首次采用基于唯一性定理的解析法和迭代法相结合的方法来求解表面电流，此外，将分离变量法应用于泊松方程的解析解来求解单定子、单转子表贴式结构的轴向磁通永磁同步电机的气隙磁通密度，并通过三维有限元分析，验证了方法的有效性。

针对双定子、单转子表面嵌入式轴向磁通永磁电机的解析模型进行了预测和创建，结合了磁场叠加定理、等效面电流的概念，将盘式电机等效成直线电机求解其空载工况下的气隙磁密，并根据电磁场的唯一性理论，给出了满足泊松方程的边界条件，求解了三相定子电枢绕组作用下的气隙磁密。空载下的气隙磁场与电枢绕组作用下的气隙磁场叠加来预测电机负载工况下的气隙磁场。最后用三维有限元仿真计算结果与解析法进行了比较，验证了解析法的正确性和有效性。

1 盘式电机空载解析计算

针对1台24槽22极双定子、单转子表面嵌入式盘式电机样机进行分析。样机的三维有限元仿真如图1所示。

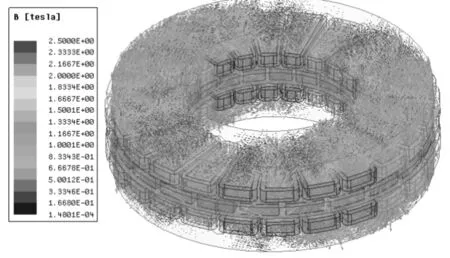
图1 盘式电机磁密矢量分布图

样机的相关技术指标和结构参数如表1所示。

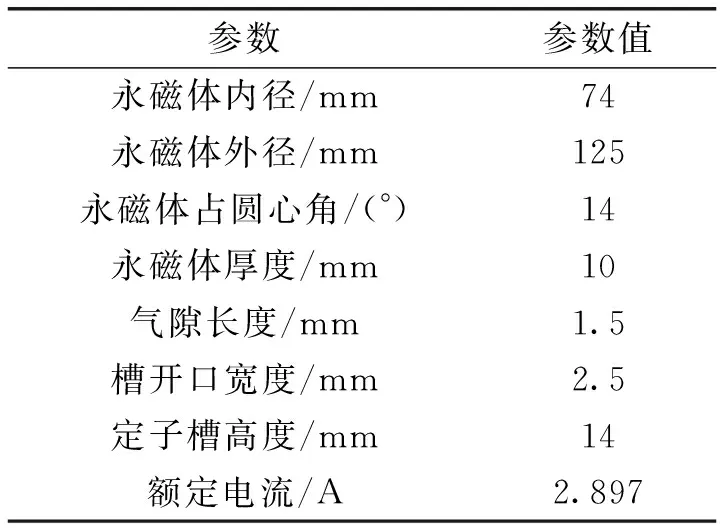
表1 样机相关技术指标和结构参数

1.1 等效电机模型

由于盘式电机与直线电机气隙磁场主要产生在轴向，因此将盘式电机等效成直线电机，来求解其气隙磁场就变得简单快捷。将盘式电机沿平均半径处展开，延展等效成直线电机。

其中一个永磁体示意图如图2所示，Rn，Rw分别是永磁体的内径和外径。a为平均半径处截面长度。

将盘式电机等效成直线电机后，建立了相应的等效面电流解析模型，定子开槽效应对气隙磁密影响不大，所以忽略齿槽效应影响。

最后为了简化分析，对轴向磁通永磁电机模型进行以下假设：①忽略铁心磁阻和铁心饱和。②忽略端部效应的影响。

1.2 空载解析模型气隙磁场计算

通过把轴向磁通永磁同步电机等效成直线电机后，为了有效快速的求解空载状态下盘式电机的气隙磁场，采用了等效面电流法建立了相应解析模型求解了盘式电机空载工况下的气隙磁场。

当盘式电机沿截面剖开后，就可以等效成矩形永磁体的直线电机了。应用面电流等效永磁体的具体方法：用一种材料代替永磁体，这种材料的磁导率为μ0μr，然后在永磁体平行于充磁方向的两边添加密度为Hc′的面电流，其中应保证面电流和永磁体产生的磁场方向一致[15]。最终建立了运用等效面电流法求解盘式电机空载工况下气隙磁场的解析计算模型，如图3所示。

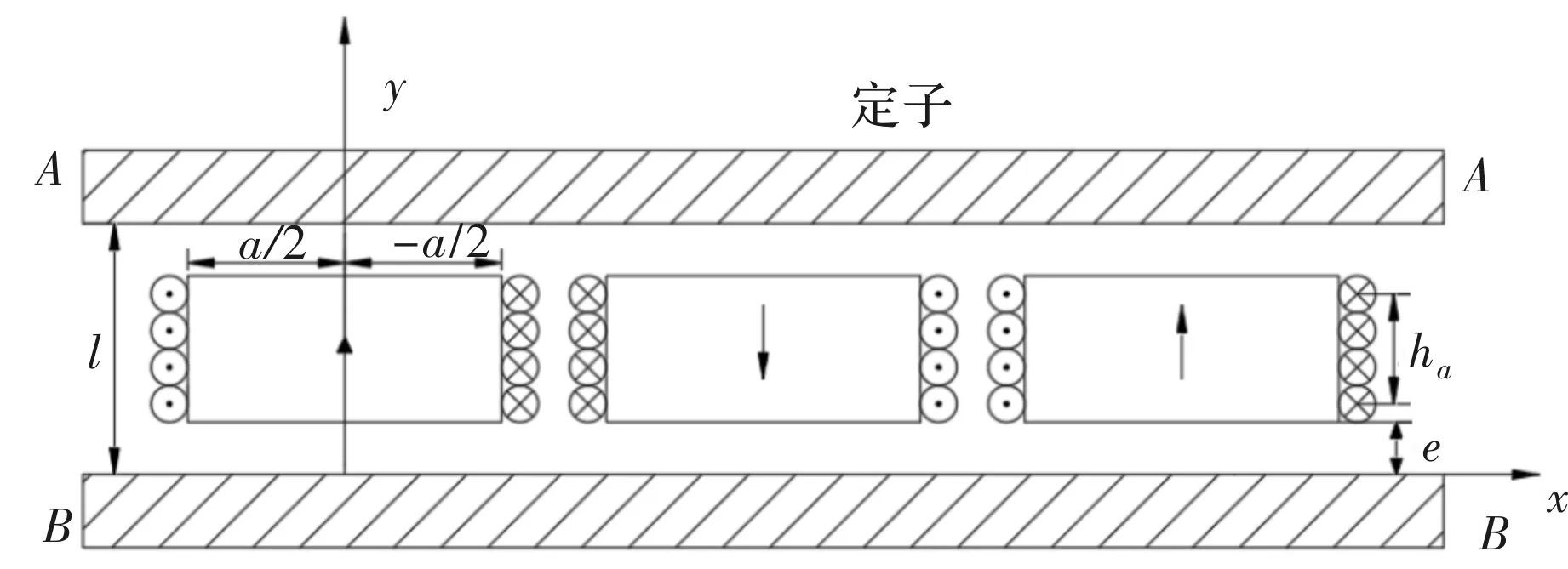
图3 空载工况下的等效面电流解析模型

根据等效面电流模型的建立，设该面电流的距离微元为de，面电流dha=Hc′de，永磁体厚度为ha，令s=a/2，极距为，利用磁场叠加原理进行磁场计算，那么2p个永磁体沿y方向对距离微元积分可得永磁体在平均半径中间气隙处产生的切向和轴向气隙磁密如式(1)和式(2)所示。

(1)

(2)

2 电枢绕组气隙磁场解析模型

在研究轴向磁通永磁同步电机气隙磁场分布时会受到永磁体和定子电枢磁场的共同影响，因此，对电枢绕组产生的磁场进行研究计算能更准确的分析电机负载工况下的气隙磁场。根据电磁场理论中的唯一性定理，给出了满足泊松方程的边界条件，并将分离变量法应用于泊松方程的解析解来计算气隙磁场。将样机进行了绕组分相，给出了每个槽内电枢线圈相电流方向的二维简化模型。最后建立了相应的电枢绕组作用下的气隙磁场解析模型。

2.1 电枢绕组

样机为5 kW盘式永磁同步电机，其中极对数p=11，定子齿数Z=24；定子铁心由硅钢片叠压而成，电机绕组直接绕在定子铁心上，节距Y=1，并联路数1，双层绕组。

通过对盘式电机的定子电枢绕组分相后，就可以知道每相电枢线圈的电流方向，应为电机采用双层绕组，从而就可以确定每个定子槽里面的两条有效边的相数和电流流向。下面以A+相和B+相两个线圈共同所在的定子槽为槽1，逆时针连续给出了6个槽内两条有效边电流方向(电流流进定子槽方向为正，流出定子槽方向为负)的简化示意图，如图4所示。

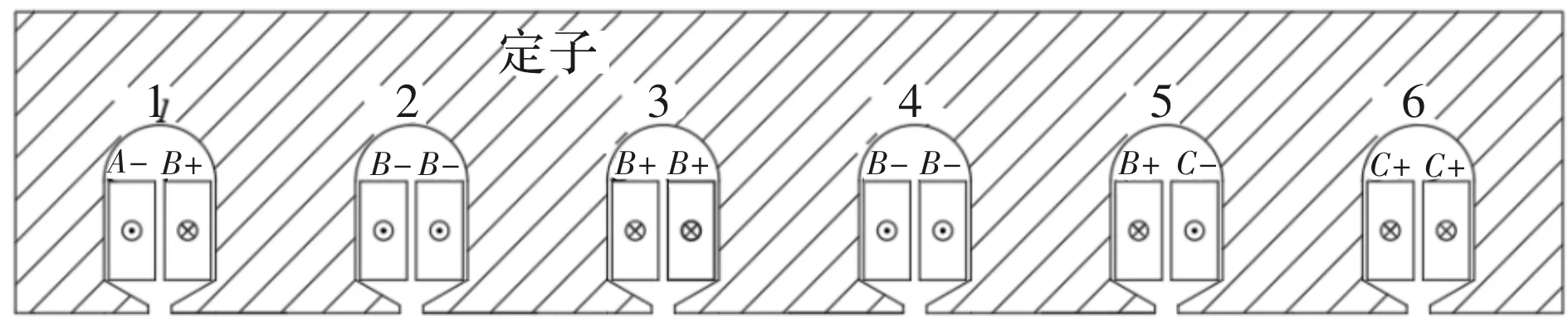
图4 定子槽内两条有效边电流流向图

2.2 电枢绕组单独作用下的气隙磁场解析模型

根据定子24个槽内的电枢绕组线圈分布及各个槽内两条有效边的电流方向，建立了相关的等效简化模型，如图5所示，解析计算了每个槽当中的每条有效边在平均半径气隙处的气隙磁场，在应用磁场叠加定理得到了整个盘式电机电枢绕组的轴向气隙磁场。

图5 定子电枢绕组激励下的气隙磁场解析模型

为了求解电枢电流在气隙产生的磁场，那么需要去掉永磁体，求解仅用电枢绕组作用下产生的气隙磁场。给出了相应的区域条件来求解泊松方程，假设有两个区域为式(3)，模型电机和选定区域如图5所示。

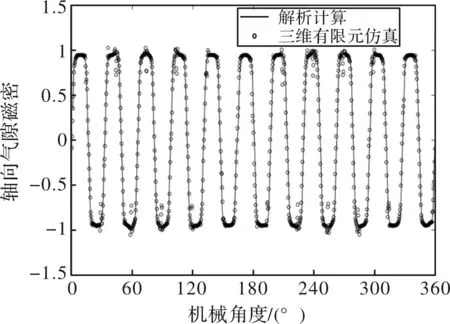
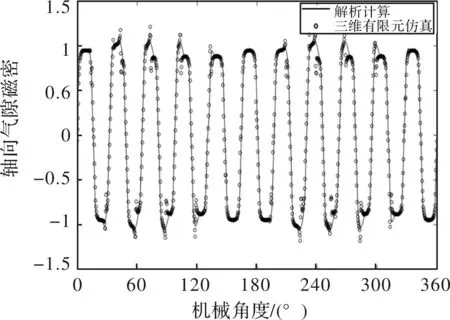
(区域I(永磁体)：0区域II(气隙):ha+2e

(3)

其中，γ=ha+2e+2h。

边界条件和控制方程分别为式(4)和式(5)所示。

(4)

(5)

式中,Jar为电枢电流密度。Jar中一个线圈电流的作用在式(6)以傅里叶展开形式表示。

(6)

式中,Ix为线圈相电流，Nc为线圈的匝数，S为槽面积，单位为平方毫米。γso为角度制下的槽口宽度。

在式(5)的解中应用分离变量法，则电枢绕组作用下的轴向和切向气隙磁密分量分别如式(7)和式(8)所示。

(7)

(8)

式中，

3 解析分析与三维有限元仿真验证

由于盘式电机的特殊结构，气隙磁场主要产生在轴向，所以计算了盘式电机在平均半径中间气隙处的轴向磁密，并用有限元仿真进行了对比验证。

图6和图7分别为空载永磁体作用下和三相定子电枢绕组单独作用时气隙磁场波形对比图。

图6 永磁体单独作用时轴向气隙磁场波形对比图

图7 三相定子绕组单独作用时轴向气隙磁场波形对比图

最后通过解析法求解的永磁体单独空载状态下在轴向产生的气隙磁场与三相定子电枢绕组产生的轴向气隙磁场叠加得到负载状态下的气隙磁密与三维有限元仿真进行了对比验证，如图8所示。

图8 负载情况下轴向气隙磁场波形对比图

通过三维有限元仿真结果与解析计算结果的对比验证，由图可见，解析方法的计算结果与三维有限元仿真具有良好的一致性。

4 结 论

提出了针对双定子、单转子表面嵌入式轴向磁通永磁同步电机求解其气隙磁场的解析方法。

(1)建立了基于等效面电流的解析模型，求解空载状态下的盘式电机气隙磁场气隙磁密和三相定子电枢双层绕组单独作用下的电枢反应气隙磁密。

(2)解析计算了负载工况下盘式电机的气隙磁场分布。并与相应的有限元模型计算结果进行了对比，在有限元分析计算中是考虑了铁心磁阻，因此解析计算结果和有限元计算结果有一定的误差，误差小于2.7%。

由于解析分析方法在保证精度的前提下缩短了大量计算时间，解决了复杂模型三维电机的仿真问题。所以提出的解析方法为轴向磁通永磁同步电机的优化设计和解析分析提供了基本手段。