平行四边形面积“变形记”

文／江苏省常州市武进区湖塘实验中学 刘骐祯

在学习了“中心对称图形——平行四边形”这一章后，我们认识了旋转运动与中心对称，深入了解了平行四边形的定义、性质与判定。为什么说是“深入了解”呢？其实，我们在小学就已经初步认识了平行四边形及其面积的计算方法，并在平行四边形面积公式的基础上，推导出了三角形的面积公式，即用两个完全一样的三角形能拼成一个平行四边形。可是，我们并没有看见具体的证明过程。下面，我就借助平行四边形来重新证明三角形的面积公式，并借此感受上面提出的问题。

如图1，在△ABC中，AH是△ABC的高，O为△ABC的边AC的中点，将△ABC绕点O旋转180°，B的对应点为B′。

如图2，连接OB、OB′。∵O为AC的中点，∴OA=OC。∵△ABC绕点O旋转180°，∴B、O、B′三点共线且BO=B′O，∴四边形AB′CB是平行四边形（对角线互相平分的四边形是平行四边形）。∵△ABC绕点O旋转180°得到△AB′C，∴△ABC≌△CB′A，∴S△ABC=S△AB′C，∴S△ABC=因此，三角形的面积公式为S=

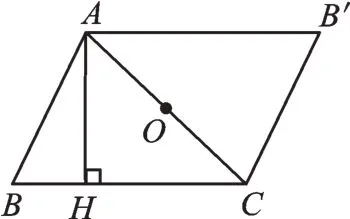
图1

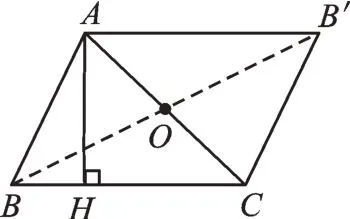
图2

孔子云：“温故而知新，可以为师矣。”在今后的数学学习中，我们要学会放慢脚步，尝试用新的高度、新的角度和新的思路来回顾所学的知识，将未知转化成已知，激发新的火花。这也是我们学习数学必须持有的态度哦！同学们，不妨和我一样再尝试重新推导梯形的面积公式吧！

教师点评

小作者善于思考，勇于提问，思维严谨，通过将三角形转化为平行四边形，重新推导了三角形面积公式，完善了知识体系。愿你坚持善思、善问、善辩、善证，演绎数学精彩！