基于抽水和荷载综合作用的沉降自回归分布滞后模型

施 颢

(江苏省地理基础地理信息中心,江苏 南京 210013)

0 引言

城市地面沉降是人为因素和自然因素综合作用下的一种区域性地面高程下降的地质灾害现象,严重影响着城市基础设施建设。目前,国内外专家学者对沉降影响因素的研究表明,抽取地下水和城市建筑荷载对地面沉降的影响最大[1-3]。

本文分别对抽取地下水和建筑荷载引起的地面沉降进行分析,引入自回归分布滞后模型,模拟在抽水和荷载两种因素综合作用下沉降的滞后性,建立了沉降自回归分布滞后模型[4-6],实例计算表明,该模型拟合预测精度较好,可以运用到具有相同地质条件地区的沉降预测中。

1 模型建立

大量研究表明,抽取地下水引起的地下水位变化会对地面沉降产生长期的影响,这种影响会表现出一定监测周期的滞后性,即水位变化和地面沉降量不同步。同时,城市建筑物群对地面施加的荷载,引起土壤压实,产生沉降。随着建筑物荷载在不断地变化,地面沉降量会根据荷载的分布以及强度在之后的监测周期表现出相应的变化。

综上所述,地面沉降的滞后性表现为前一个监测周期的地下水位值和建筑物荷载对沉降量起着决定作用,即:

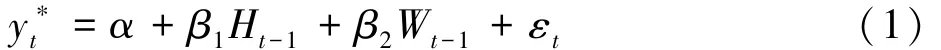
式中,为沉降量预测值;Ht-1为前一个监测周期的地下水位值;Wt-1为前一个监测周期的建筑物荷载;εt为误差项;α为常数;β1,β2为模型参数。

由于沉降滞后性的存在,与真实的沉降量会有一定的误差。因此,引入补偿系数ξ进行调整,关系式如下:

其中,ξ的取值范围在0~1之间,ξ越接近于1,表示预测值和真实的沉降量间的误差越小。

式(2)可调整为:

上式表明真实沉降量yt可由预测值y*t和前一期沉降量yt-1的加权和表示。

将式(1)代入(3)可得:

式中,α′,β′1,β′2,φ模型系数;ε′t为误差项。

上式为最终形式的基于抽水和荷载影响的沉降自回归分布滞后模型,在求得模型系数和误差项后,代入前一监测周期的水位值和建筑荷载即可对沉降量进行预测。

2 实例分析

现有某地5年多时间共64期的沉降量监测数据和对应监测周期的水位监测数据及建筑荷载数据,沉降量如图1所示。

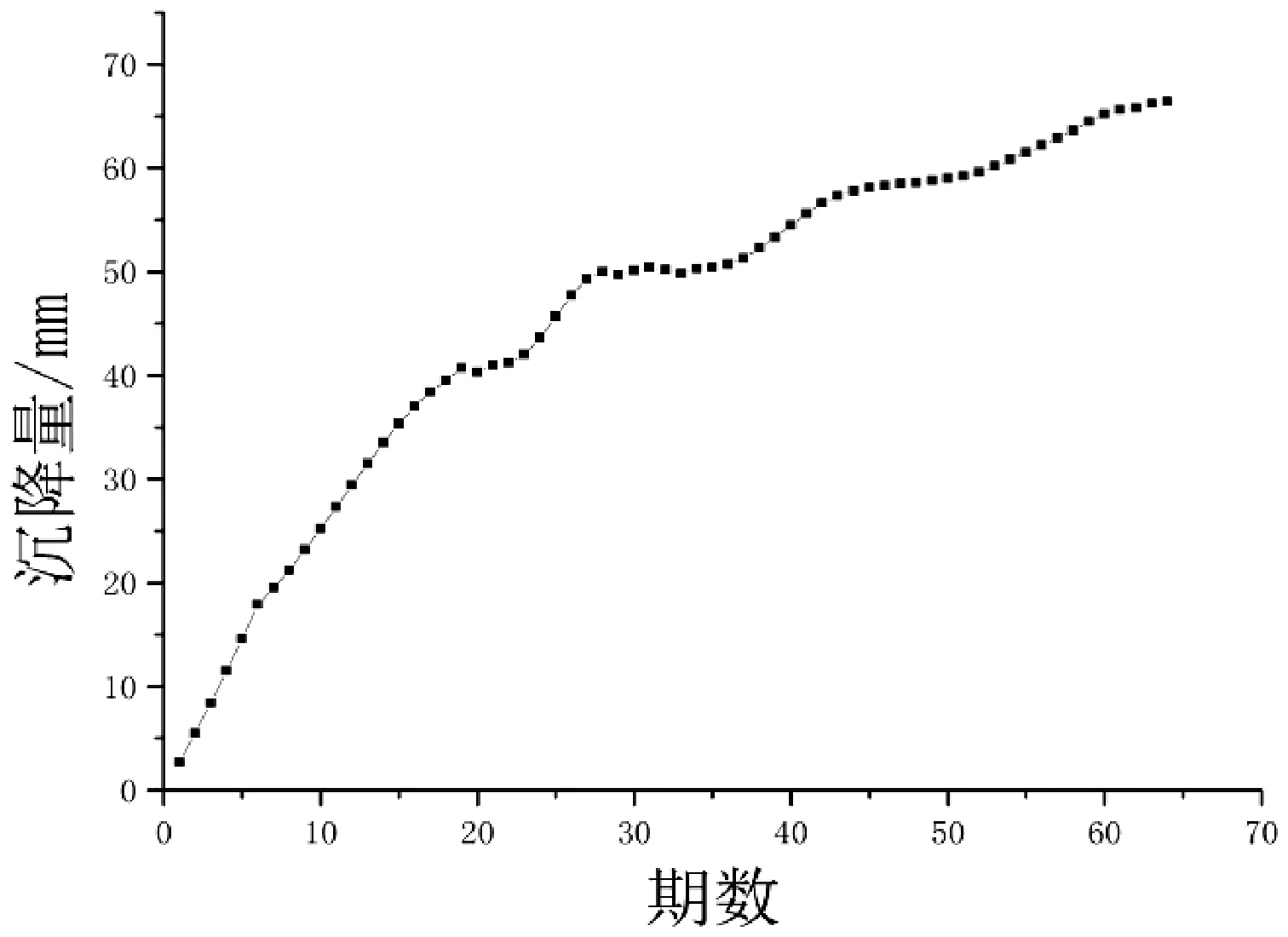
图1 某地沉降量数据

为了便于后文对模型拟合和预测精度进行分析,将64期数据划分为两部分:前52期为历史数据,用于拟合求模型参数;后12期作为模型建立后的预测检核数据。

利用Eviews软件的分位数回归功能进行回归分析,得到模型各参数后代入式(4)得到最终的自回归滞后模型,模型在0.3,0.5,0.7和0.9四个典型分位数下的拟合图如图2所示。

图2 不同分位数下模型拟合结果

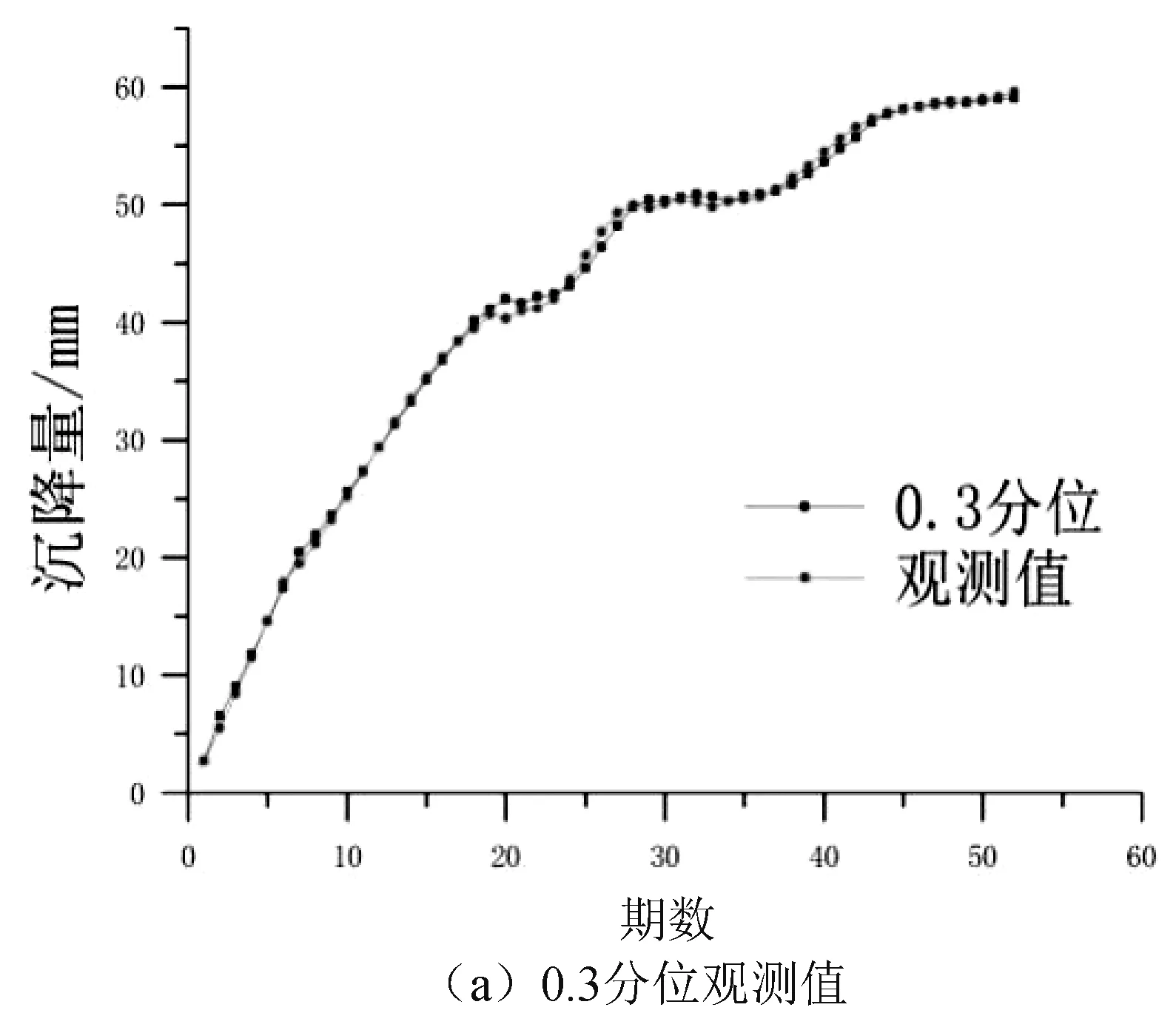
从图2和表1可以看出,0.3,0.5和0.7分位下的模型拟合效果好,平均误差相接近,0.9分位拟合效果最差,误差也最大。因此,本文选取精度最高的0.5分位下回归分析得到的参数代入式(4)得到最后的沉降自回归分布滞后模型对后12期沉降量进行预测。

表1 各分位数下模型拟合平均误差

3 数据检核

为了检核模型预测精度,结合一次、二次和三次指数平滑法对沉降量进预测,结果如表2所示。

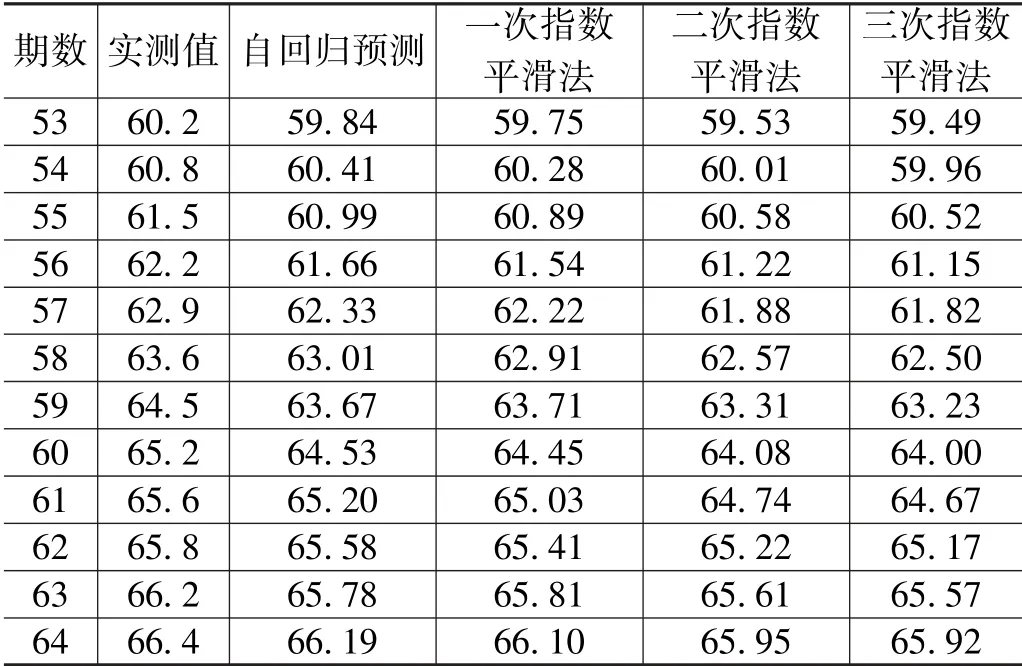
表2 自回归滞后预测模型和指数平滑法预测结果(单位:mm)

从表2的12期预测值可以看出,考虑抽水和荷载综合作用的自回归滞后模型对沉降量的预测效果最好,优于指数平滑法。

4 结语

针对地面沉降受地下水位变化和建筑荷载影响表现出的滞后性,引入自回归分布滞后模型,建立沉降量与地下水位和地面建筑荷载之间的关系式,结合实地监测数据进行拟合预测。结果表明,考虑地下水位和建筑荷载变化的自回归分布滞后模型能很好地模拟地面沉降的滞后性,且预测精度优于指数平滑法。