基于改进神经网络的空间机械臂阻抗控制方法

戚毅凡，贾英宏，赵宝山，钟睿，洪闻青

1. 昆明物理研究所，昆明 650223

2. 北京航空航天大学 宇航学院，北京 100191

3. 天津航天机电设备研究所 天津市微低重力环境模拟技术重点实验室，天津 300301

1 引言

在轨服务技术是航天领域的热点研究问题之一，而空间机械臂是空间任务中不可或缺的装备。空间机械臂在执行零件对接拆装、维修、捕获及释放等操作时会与环境发生接触，空间机械臂末端与环境会存在较大的接触力。为了确保目标或机械臂本身不被损坏以及任务的顺利进行，必须对空间机械臂进行柔顺控制[1]。

机械臂柔顺控制包括被动柔顺控制和主动柔顺控制[2]。被动柔顺控制的力控制精度较低，对环境的适应能力有限，因而主动柔顺控制是主要研究方向。主动柔顺控制主要分为两类：力/位混合控制和阻抗控制。力/位混合控制就是在一定规则下将力反馈与位置反馈相结合，以同时满足任务中位置和力的约束条件。其原理是在笛卡尔坐标系下将机械臂末端的运动空间分解为约束空间和无约束空间，在不受约束空间上进行位置控制，在约束空间上进行力控制[3]。文献[4]提出了阻抗控制算法，该算法建立了力、位置、速度的阻抗关系式，仅需要一个控制策略即可同时控制力和位置。阻抗控制将力和位置控制纳入同一控制体系，相比力/位混合控制，阻抗控制计算量更小，控制更容易实现，且研究的成熟度更高。故本文使用阻抗控制算法作为柔顺控制方法。

使用阻抗算法实现精准的力控制要求获得精确的环境信息，例如环境位置、环境刚度和环境阻尼等[5]。然而空间机械臂在执行任务时环境复杂多变，环境信息难以准确测量或辨识，获得精确的环境信息难以实现，为此众多学者针对该问题进行了研究。文献[6]在传统阻抗控制中引入了自适应控制方法，基于迭代思想弥补环境信息不确定所带来的影响，使控制器对环境的适应能力增强。文献[7]将鲁棒控制与阻抗控制相结合，基于函数逼近技术设计了鲁棒阻抗控制器，并在Puma560机器人上验证了该控制器的有效性。

也有学者通过实时调整阻抗参数，来解决环境信息不确定下的空间机械臂阻抗控制问题。阻抗参数的选择决定了控制器的柔顺特性，若阻抗参数能随环境实时调整，则阻抗控制器的柔顺控制效果会优于阻抗参数固定的情况[8]。文献[9]提出了一种在未知环境下模糊自适应阻抗控制，通过接触力反馈调整阻抗参数来适应未知环境。绝大多数研究在解决环境信息不确定下的空间机械臂阻抗控制问题时，通常将碰撞模型假设为简单的弹簧模型或是弹簧阻尼模型，而真实的碰撞模型是更复杂的、更难以解析的非线性模型[10]。若碰撞模型未知或建立不准确，以上研究中调整阻抗参数的自适应算法将失效，控制器的柔顺控制效果无法得到保障。

神经网络凭借非线性拟合的特性被引入到自动化控制领域中，与传统控制器相比，神经网络控制器不受被控对象模型建立的影响，其适应性和鲁棒性均较强[11]。若能将神经网络引入到柔顺控制系统中，并根据机械臂末端反馈信息对阻抗参数进行实时调整，则能避免由于碰撞模型未知及空间中环境的不确定因素对柔顺算法产生的不利影响。当下已有许多学者将神经网络与阻抗算法相结合，对空间机械臂进行控制。文献[12]提出了一种基于BP神经网络的自适应阻抗控制，BP神经网络根据环境刚度和位置的变化通过补偿阻抗控制器的误差来校正机械臂末端的位置。文献[13]将RBF神经网络应用于改进后的阻抗关系，对系统的未知部分进行补充，提高了所设计控制器的跟踪性能。

但将传统神经网络应用于阻抗参数实时调整存在诸多问题，例如学习时间冗长、网络参数选择无具体参考公式等[14]。例如传统BP神经网络通常使用逆梯度下降法完成训练，收敛速度慢，易陷入局部最优[15]，故无法将阻抗参数实时调整到最优数值。针对环境信息不确定、真实碰撞模型复杂且未知、传统神经网络收敛速度慢且易陷入局部最优等问题，本文将粒子群优化算法(particle swarm optimization，PSO)与传统神经网络结合，提出了一种基于改进神经网络的阻抗控制方法。该方法无需准确的环境信息，也不需要碰撞模型的先验知识，利用粒子群优化算法调整神经网络中的权值矩阵，改善传统BP神经网络的寻优性能。改进后的神经网络根据机械臂末端反馈的信息在线调整阻抗参数，以获得更好的控制性能和控制精度。所设计的粒子群优化BP神经网络阻抗控制器(PSO-BP阻抗控制器)能有效降低最大接触力，减小稳态力控制误差，提高控制系统的响应速度，且不依赖精确的环境信息，具有较强的抗干扰能力。

2 空间机械臂建模及阻抗控制

2.1 空间机械臂建模

本文以如图1所示的平面二自由度机械臂系统作为研究对象，系统由卫星基座与二自由度机械臂构成。

图1 二自由度机械臂系统Fig.1 2-DOF manipulator system

假设卫星基座受控良好，位置与姿态保持固定状态。此情况下，空间机械臂的柔顺控制可以类比固定基座机械臂，即卫星本体坐标系近似于惯性坐标系[16]。机械臂连杆视为细杆，连杆间由单自由度的旋转关节连接，整个系统为二自由度系统。机械臂末端接触卫星基座上一平板，平板与卫星基座固连且垂直于卫星基座表面。如上机械臂系统的动力学方程可以写为：

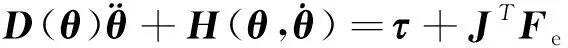
(1)

式中：τ为关节控制力矩；θ为关节转角；D为正定对称的质量阵；H为离心力和哥氏力向量；Fe为机械臂末端与环境的接触力；J为雅克比矩阵。机械臂正运动学即由各关节转角计算获得机械臂末端位置，其可通过几何关系推导得到。将正运动学方程求导，便可获得机械臂末端速度的计算式

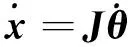
(2)

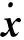
2.2 阻抗控制算法及接触过程分析

阻抗控制算法将环境与机械臂纳入一个统一的控制体系，当机械臂未接触环境时，可以根据位置误差进行轨迹规划。当机械臂与环境接触产生接触力时，阻抗算法就能响应该接触力，使机械臂系统在位置控制和力控制之间达到一个平衡状态。阻抗关系式通常使用二阶形式[18]：

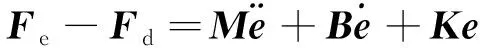
(3)

式中：Fd为机械臂末端期望接触力；M、B、K为阻抗参数，分别为惯性系数矩阵、阻尼系数矩阵和刚度系数矩阵，均为正定对角阵；位置误差e=xd-x，x为机械臂末端位置，xd为机械臂末端期望位置。使用计算控制力矩法并结合空间机械臂逆动力学方程设计阻抗控制器[19]，控制器输出的关节控制力矩τm为：

(4)

若碰撞模型已知，则可根据式(1)～(4)分析空间机械臂与环境接触过程中的动态响应性能。常用的碰撞模型包括K模型、Kelvin-Voigt模型(K-V模型)和Hunt-Crossley模型(H-C模型)[20]。K模型假设接触力仅由碰撞物体的局部接触形变导致，接触力大小与形变量成正比；K-V模型将碰撞模型等效为弹簧阻尼模型；H-C模型假设碰撞模型为更复杂的非线性模型。K模型、K-V模型、H-C模型的复杂程度依次递增，接触力计算也越接近真实碰撞情况。在机械臂柔顺控制领域中，由于更注重控制算法的研究，所以碰撞模型通常选用较简单的K模型和K-V模型，计算得到的接触力不能反映真实的碰撞过程。故本文使用更接近真实碰撞情况的H-C模型计算接触力，其计算公式为：

(5)

式中：δ=x-xe，xe为环境位置；Khc和Bhc分别为环境刚度矩阵和环境阻尼矩阵，均为正定对角阵，表示接触力可以在任意方向上解耦；指数n为模型的非线性度。H-C模型仅为仿真时计算空间机械臂末端接触力使用，在控制过程中碰撞模型未知，可将式(5)表示为：

(6)

式中：函数g为一个未知的非线性函数。将式(3)(4)(6)代入式(2)即可获得发生碰撞时机械臂系统的闭环方程

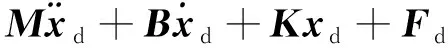
(7)

由式(7)，机械臂末端稳态位置xss满足

(8)

稳态接触力Fss与稳态位置xss存在非线性关系

(9)

由式(8)(9)可以计算稳态力误差EF为：

EF=Kxd-Kxss

(10)

若要使稳态力误差EF=0，则期望轨迹需要满足

xd=xss

(11)

在碰撞模型未知、环境信息不确定的情况下机械臂末端稳态位置xss不能求解。环境刚度的数值通常较大，期望轨迹较小的偏差就会导致较大的力控制误差，这也是该情况下传统阻抗控制难以实现精准力控制的原因。对于传统阻抗控制，阻抗参数的选择往往是根据经验决定，在整个控制过程中视为固定值。但阻抗参数的选择与机械臂模型、环境模型有较强的依赖关系，所以传统阻抗控制系统的稳态误差较大，而且系统的鲁棒性较差。由式(10)(11)还发现，若阻抗参数能进行合适的调整，则可以降低稳态力误差，实现精准的力控制。下文将使用改进后的神经网络对阻抗参数进行在线调整，以提高力控制精确度。

3 基于改进神经网络的阻抗控制

3.1 粒子群优化算法

文献[21]提出粒子群优化算法，PSO算法初始化一群随机粒子，通过迭代在随机解中寻找最优解。粒子群优化的基本原理为[22]：假设在一个D维空间中存在一个由N个粒子组成的种群，在求解最优值的过程中，每个粒子通过自身的历史最优位置和种群的历史最优位置，调整自身的位置和速度，使自身向全局最优解靠近。定义第i个粒子的位置向量为xi=(xi1xi2…xiD)，速度向量为vi=(vi1vi2…viD)，历史最优位置为pi=(pi1pi2…piD)，整个种群的历史最优位置为pg=(pg1pg2…pgD)。在迭代过程中，每一个粒子根据以下公式对自身的位置和速度进行更新：

(12)

(13)

式中：i=1,2,…,N;d=1,2,…,D;ω为惯性因数；c1、c2为加速系数，均为非负常数，加速系数的合理选择可以提高寻优速度并且避免陷入局部最优；r1、r2分别为两个[0,1]之间的随机数。式(12)(13)表示第i个粒子由第k代进化到第k+1代速度和位置的更新规则。粒子速度通常被限制在一个范围之内，vid∈[-vmax,+vmax]，避免因其速度过大而搜索远离最优解或速度过小陷入局部最优。同样，粒子位置也被限制于一个范围之内，xid∈[-xmax,+xmax]。xmax、vmax通常根据经验设定。粒子群优化的结束条件一般为：达到最大迭代次数kmax或全局极值对应的适应度值小于目标适应度阈值[23]。

3.2 PSO-BP阻抗控制器设计

在碰撞模型未知、环境信息不确定的情况下，空间机械臂难以实现准确的力控制。传统神经网络难以实现理想的自适应控制，其原因为：学习或训练时间较长，无法满足控制快速性的要求；控制结果与系统的稳定性受权值矩阵初始值的影响较大；易陷入局部最优，无法找到满足要求的全局最优解。基于以上原因，本文对传统BP神经网络进行改进，引入PSO算法作为神经网络的学习算法，并将改进后的神经网络与阻抗控制结合，设计PSO-BP阻抗控制器，控制器结构如图2所示。

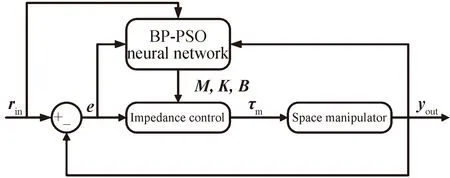
图2 PSO-BP阻抗控制器结构示意Fig.2 Structure of PSO-BP impedance controller

图3 PSO-BP神经网络结构示意Fig.3 Structure of PSO-BP neural network

1)随机初始化输入权值矩阵win和输出权值矩阵wout，设置神经网络各层节点个数：输入层神经元数I=3、隐层神经元数H=5、输出层神经元数J=3。神经网络的输入信号xin、输入权值矩阵win和输出权值矩阵wout的具体表达形式为：xin=[xi],win=[vih],wout=[whj]

其中，i=1,2,…,I；h=1,2,…,H；j=1,2,…,J。 2)由期望轨迹、期望力、机械臂末端轨迹和接触力构成神经网络的输入信号：

3)将输入信号传递给神经网络的输入层，由输入权值矩阵win计算隐层第h个神经元的输入αh：

αh=xivih

4)隐层将输入信号αh输入激活函数后输出，隐层激活函数为tanh函数，具体计算过程为：

5)将隐层输出信号传递给输出层，由输出权值矩阵wout计算输出层第j个神经元的输入βj：

βj=bhwhj

6)输出层将信号βj输入激活函数后输出，输出激活函数为sigmoid函数，其具体算法为：

其中，z1=M，z2=B，z3=K。

7)根据PSO-BP神经网络输出的阻抗参数计算关节控制力矩τm，并根据要求对其进行限幅，之后将关节控制力矩输入到空间机械臂系统中。

8)粒子群开始寻优，粒子群维度由输入权值矩阵win和输出权值矩阵wout中的元素个数决定，定义粒子的适应度函数f为：

9)根据位置和速度更新公式，得到下一代粒子群的位置和速度，并计算各粒子的适应度，更新个体极值与全局极值。

10)当全局极值大于或等于所设定的目标值时，返回步骤8)。若全局极值小于设定的目标值或达到迭代次数上限，寻优结束，当前粒子位置即代表输入权值矩阵win和输出权值矩阵wout中每一个元素的最优解。

将输入权值矩阵win和输出权值矩阵wout返回至PSO-BP神经网络中，重复步骤3)～7)计算最优阻抗参数，对空间机械臂系统进行柔顺控制。

4 数值分析

图4 机械臂末端x方向接触力误差Fig.4 Contact force error on tip of manipulator in x direction

图5 机械臂末端x方向位置误差Fig.5 Position error of tip of manipulator in x direction

图6 惯性系数的变化Fig.6 Variations of inertial coefficient

图7 阻尼系数的变化Fig.7 Variations of damping coefficient

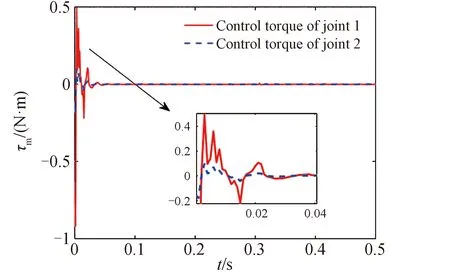
图9 PSO-BP阻抗控制器关节控制力矩Fig.9 Control torques of PSO-BP impedance controller

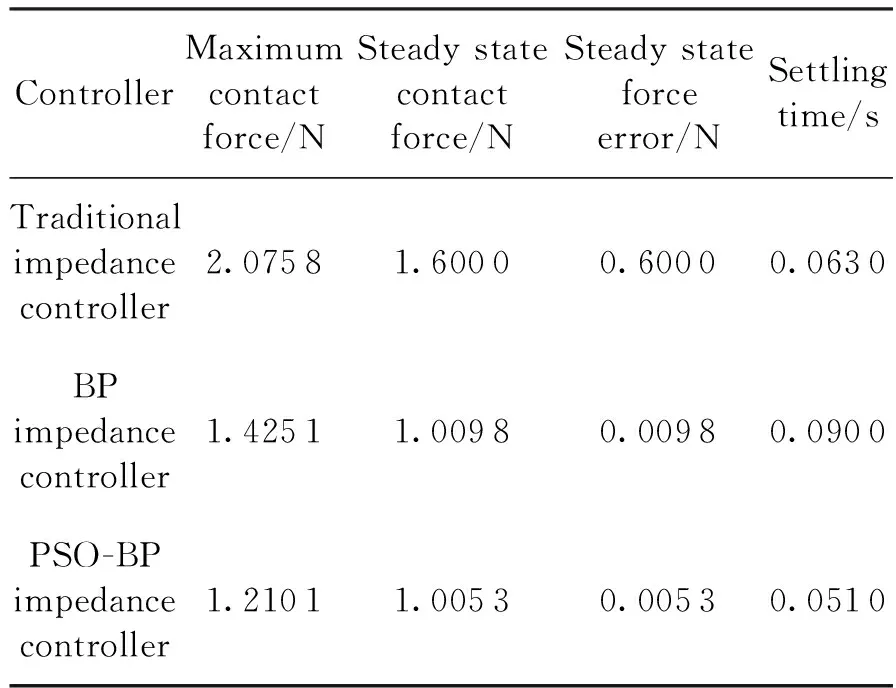
表1 接触力动态响应

由仿真结果可见，相较于传统阻抗控制器和BP阻抗控制器，本文提出的PSO-BP阻抗控制器的机械臂末端位置控制误差和接触力控制误差最小(图4、图5)，与传统阻抗控制器相比降低了99.1%；此外，PSO-BP阻抗控制器实现了更小的最大接触力和更短的调节时间(图4、表1)，与传统阻抗控制器相比分别降低了41.7%和19.0%，柔顺控制效果得到显著提升。在初始阶段，由于粒子群处于初始化阶段，寻优难度较大，在线调整的惯性系数、阻尼系数和刚度系数出现了幅值较大的调节过程(图6～8)，控制力矩也出现高频振荡(图9)；但当粒子群的速度和位置经过较短时间的更新后，就能快速地寻找到全局最优方向，优化和控制效果随之平稳。为了考察PSO-BP阻抗控制器的抗干扰能力，在仿真中的接触力反馈通道设置了一个正弦干扰信号Fint=0.15sin (180t)，机械臂末端位置误差及接触力的仿真结果如图10、图11所示。

图10 存在干扰情况下x方向的机械臂末端接触力误差Fig.10 Contact force error of tip of manipulator with interference in x direction

图11 存在干扰情况下机械臂末端x方向的位置误差Fig.11 Position error of tip of manipulator with interference in x direction

由图10、图11可见，在接触力反馈存在干扰信号的情况下，BP阻抗控制器和PSO-BP阻抗控制器的机械臂末端接触力和位置控制精度均显著优于传统阻抗控制器，而PSO-BP阻抗控制器在力反馈信号受到干扰时位置误差和接触力误差波动最小，位置控制和力控制更为稳定，表现出较强的抗干扰能力。

5 结论

本文针对环境信息不确定和碰撞模型未知情况下的空间机械臂柔顺控制问题，结合文献[21-22]的粒子群优化算法对神经网络进行改进，将文献[18]的阻抗控制方法与改进后的神经网络相结合，提出了一种改进型神经网络阻抗控制方法，得到的结论如下：

1)针对传统BP神经网络学习时间长、易陷入局部优化等问题，利用PSO算法调整神经网络中的权值矩阵，改善传统BP神经网络的寻优性能。

2)将PSO-BP神经网络与阻抗控制相结合，设计了PSO-BP阻抗控制器。该控制器可在无碰撞模型先验知识、不依赖环境信息的情况下，利用空间机械臂末端位置和力的信息反馈，在线调整阻抗参数。

3)数值仿真结果表明，相比传统阻抗控制器和BP阻抗控制器，本文所设计的PSO-BP控制器对机械臂末端的位置控制和接触力控制精度更高，最大接触力更小，且对于力反馈干扰信号具有更强的抗干扰能力。

4)本文所提出的算法有效提升了控制器的柔顺控制性能，但对硬件的计算能力要求较高。在后续研究中，可对算法进行逻辑优化进而减少计算量，提高该方法的实用性能。