基于人工表面等离激元周期调制的漏波天线设计*
2022-04-20王萌彭玉婷马慧锋
王萌,彭玉婷,马慧锋
(东南大学毫米波国家重点实验室,江苏 南京 210096)
0 引言
在光频段,由于金属的特性表现为等离子体,介电常数为负值,表面等离激元(SPPs,Surface Plasmon Polaritons)可以在金属-介质界面上以表面波的形式传播[1],这种特殊的表面波具有明显的波长压缩效果和高度场束缚特性,因此有利于实现等离激元光子学器件的小型化设计。然而,当工作频率下降到微波、毫米波或太赫兹波段,金属表现出理想电导体(PECs,Perfectly Electrical Conductors)特性,此时在金属-介质交界处不再支持自然SPPs的表面波模式。2004年Pendry爵士等人[2-5]在金属表面刻蚀了按亚波长间距排列的空气槽,从而在微波段产生了类似于自然表面等离激元的表面波模式,即人工表面等离激元(SSPPs,Spoof Surface Plasmon Polaritons)。这种人工表面等离激元结构可以在低频段复现自然SPP在光波段展现出的物理性质,但是由于采用三维结构,设备体积庞大,难以与传统的射频系统集成,极大地限制了其应用。2013年二维人工表面等离激元波导结构的出现,受到了研究者们的广泛关注[6]。平面人工表面等离激元波导仅由超薄波纹金属条带组成,这不仅意味着更低的制作成本,而且有利于与传统微波电路相融合。自2014年以来,传统波导与人工表面等离激元波导间的转换结构接连被提出[7-9],在传统平面微波电路和平面人工表面等离激元之间建立了桥梁。
近年来,基于波纹金属条带结构的人工表面等离激元波导很受欢迎,利用单元结构槽深可以调制人工表面等离激元色散特性这一原理[10-12],国内外研究者们开展了许多新颖器件的设计工作,包括波导[13-15]、滤波器[16-18]、耦合器[19-20]和漏波天线[21-23]等。然而,目前该领域的研究主要关注槽深的作用,而忽略了波导周期对人工表面等离激元电磁特性的操控。漏波天线作为一种行波天线,因具有低剖面、高增益、大带宽等独特优势而备受关注。本文接下来将基于周期调制原理,设计出辐射波束角度及数量均可定制的漏波天线。
1 人工表面等离激元波导的周期特性
1.1 单元结构
人工表面等离激元波导的单元结构如图1右侧所示,选用常见的金属开槽结构,介质基板的相对介电常数为2.25,厚度为0.8 mm。单元几何尺寸的具体值为a=0.8 mm、h=4 mm、H=4.4 mm。利用电磁仿真软件CST进行本征模仿真[24],将传播方向设定为周期性边界条件,非周期方向上向外延拓一定距离后设置为理想电边界条件,然后将传播方向上的相位从0°到180°范围内进行扫描,可以得到不同调制周期下单元的色散曲线。从图中可以看出,当周期p从2.8 mm增加到15.8 mm时,渐进频率fc从12.5 GHz减小到7.4 GHz,相位常数β也更加接近光线。这意味着随着波导周期的增加,渐进频率会降低,波导对人工表面等离激元的束缚性减弱。值得注意的是,渐进频率fc是在βp=π[2-12]的条件下得到的。为了研究不同周期尺寸对人工表面等离激元电磁特性的调制作用,此处选择10 GHz作为工作频率。由图1中的色散曲线可知,p=2.8 mm、p=4.2 mm、p=9.4 mm和p=15.8 mm的人工表面等离激元波导渐进频率分别为12.5 GHz、7.5 GHz、3.34 GHz和2.02 GHz。因此,当人工表面等离激元波导的周期处于亚波长尺寸p=2.8 mm和4.2 mm时,人工表面等离激元模式可以被激发并沿着波导进行有效传输。但当周期进一步增大到p=9.4 mm和15.8 mm,在10 GHz处波导将不再支持电磁波的传输,但仅根据色散曲线无法判断SSPPs是处于反射状态还是辐射状态。为了进一步的研究,下文分别给出了周期调制的原理以及不同周期下人工表面等离激元波导的S参数曲线和电场近场分布仿真结果。
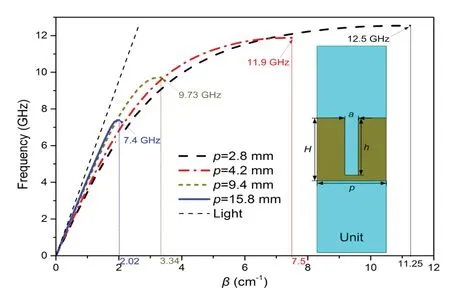
图1 SSPP波导单元结构及不同周期p对应的人工表面等离激元的色散曲线
1.2 周期调制原理
人工表面等离激元波导作为一种周期调制传输线,其周期调制特性会引入空间谐波,第N阶空间谐波的相位常数可由式(1)计算:

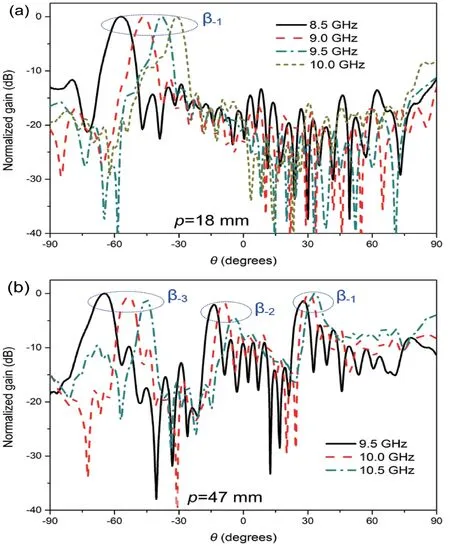
式中,β0表示基次空间谐波(N=0)的相位常数,p表示传输线的周期尺寸。因为基次谐波是慢波[25],所以其相位常数β0总是大于或等于自由空间波数k0,即β0≥k0。由式(1)可知,当周期p很小时,|βN|总是比k0大,因此所有的空间谐波均是无法辐射的慢波。然而,在p不断增大的过程中,-1阶空间谐波(N=-1)首先变成一个快波(|β-1| 基于S参数反演法[26-27]可以计算出10 GHz处具有不同周期长度的人工表面等离激元的传播常数(ksspp=β0-jα),如图2所示,其中α是衰减常数,β0是基次谐波的相位常数。只要得到基波的相位常数β0,就可以根据公式(1)计算出高次谐波的相位常数βN。10 GHz时的自由空间波数k0≈2.09,则当|βN|>k0时,人工表面等离激元为慢波;当|βN| 图2 人工表面等离激元的衰减常数和不同空间谐波的相位常数在周期长度变化下的计算值 为了对上述理论分析进行验证,接下来对不同周期下人工表面等离激元波导的电磁特性进行研究。图3(a)是采用图1中传统矩形开槽单元结构所设计的人工表面等离激元波导模型示意图,通过改变周期p来研究周期对波导电磁特性的调控作用。图3(b)、(c)是p=2.8 mm和4.2 mm下的全波仿真结果。仿真得到的S参数如图3(b)所示,由仿真结果可知,在10 GHz处p=2.8 mm和4.2 mm的波导均有较高的传输系数(S21),截止频率分别为11.9 GHz和12.5 GHz,这与图1中色散曲线结果相一致。同时,图3(c)中所展示的10 GHz处近场分布也表明这两条波导都可以有效地支持人工表面等离激元的传播,但周期为4.2 mm的波导中所传输的人工表面等离激元的波长比周期为2.8 mm中的长,这意味着随着周期的增大,电磁波的相位常数逐渐减小。 图3(d)、(e)是周期增大到p=9.4 mm(约为10 GHz处导波波长的三分之一)的人工表面等离激元波导全波仿真结果。由图3(d)仿真的S参数曲线看出此波导在10 GHz处具有低传输系数(S21<-30 dB)和高反射系数(S11>-1 dB),将无法支持人工表面等离激元的传播,表现出良好的截止特性。此外,从S参数曲线中还可以看出人工表面等离激元在此波导中的截止频率约为9.73 GHz,这与图1中的色散曲线相吻合。仿真得到的近场分布进一步证明,此时人工表面等离激元无法沿着波导传播,如图3(e)所示。 当周期进一步增大到p=15.8 mm(约为10 GHz处导波波长的一半)时,人工表面等离激元波导可再次支持电磁波的传播,但同时伴随着强烈的漏波辐射。图3(f)中的S参数曲线表明波导在10 GHz处的反射系数(S11)和传输系数(S21)均小于-10 dB,说明电磁波被高效地辐射到了自由空间中。图3(g)中的仿真电场近场分布也进一步证明,此时沿着波导传播的人工表面等离激元转化为反向漏波辐射,并且由图可知此时波束的辐射角度为-45°,这与上文中的理论计算值-46°相吻合。图1中色散曲线所表明的人工表面等离激元波导应在10 GHz处于截止状态,显然全波仿真结果与此并不一致。这是因为随着电尺寸的增加,周期结构不能再被简单地看作人工表面等离激元波导的一个单元。在这种情况下,由于周期性开槽的扰动,人工表面等离激元波导成为一条具有周期调制的非均匀传输线,从而产生漏波辐射。下面将利用此状态下的人工表面等离激元波导来设计漏波天线。 图3 不同周期下人工表面等离激元波导的全波仿真结果 从上述周期调制原理可以得知,当人工表面等离激元波导的周期尺寸增大到波长尺度时,人工表面等离激元将转换为漏波辐射到自由空间,波导转换成了漏波天线。图4中给出了六个具有不同周期的人工表面等离激元漏波天线的原理图以及在10 GHz下的三维远场辐射方向图。从公式(1)、(2)可以看出,波束的辐射角度随着周期的改变而变化。首先,在图4(a)-(c)中,分别给出了周期长度为p=15.8 mm、18 mm和22 mm的人工表面等离激元漏波天线的仿真三维远场辐射方向图,只有-1阶空间谐波产生并辐射到自由空间,且辐射的方向随周期的改变而发生变化。这与图2中的理论预测结果相一致,即只有-1阶空间谐波位于漏波辐射区域且其相位常数β-1随着周期的变化而变化。 图4(d)-(f)研究了当周期p进一步增大时,人工表面等离激元漏波天线将产生多波束辐射。由图可见,当p增加到36 mm、47 mm和60 mm时,将会产生2个、3个和4个漏波辐射波束,这是因为-2阶、-3阶和-4阶空间谐波也进入到了漏波辐射区并随着周期的增大逐个产生辐射,这也与理论预测的结果相一致。 图4 10 GHz下不同周期长度的人工表面等离激元漏波天线三维远场辐射方向图的仿真结果 为验证上述分析的正确性,对周期分别为18 mm和47 mm的人工表面等离激元漏波天线进行了加工,实物示于图5(a)中,两端用共面波导进行馈电。两个天线的S参数曲线分别展示在图5(b)和5(c)中,可以看到实测结果与仿真结果吻合良好。在10 GHz处,两个天线测试与仿真得到的S11和S21均小于-10 dB,意味着有良好的辐射性能。实测得到的xoy平面的远场辐射方向图示于图5(d)和5(e)中,对于p=18 mm 和47 mm的天线分别出现了单波束和三波束辐射,波束辐射的角度与仿真结果及理论计算值相吻合。 图5 p=18 mm和47 mm的人工表面等离激元漏波天线的仿真和测试结果 由公式(1)、(2)知,波束辐射的角度也与频率有关,因此接下来研究了漏波天线的频扫特性。从图6(a)可知,当频率从8.5 GHz增加到10 GHz时,p=18 mm的漏波天线产生的波束辐射角度从-56.9°变化到-31.1°。对于p=47 mm的多波束漏波天线,随着频率从9.5 GHz变化到10.5 GHz,其产生的三个波束分别在28°到33.1°,-13.7°到-4.2°和-64.7°到-45.2°范围内进行扫描,如图6(b)所示。值得注意的是,对于-2阶空间谐波,由于在10.5 GHz处其波束接近边射辐射,此时出现的开阻带效应会导致其增益显著下降。 图6 人工表面等离激元漏波天线在不同频率下测得的二维远场方向图 本文利用具有不同周期尺寸的超薄锯齿状人工表面等离激元波导,展示了波导周期对人工表面等离激元电磁特性的调控作用,并设计了基于人工表面等离激元的漏波天线。当波导周期为亚波长尺寸时,波导可以被看成一条均匀的传输线,从而有效地支持人工表面等离激元以表面波的形式传播。当周期增大到与导波波长尺寸相当时(如半波长或者更大的尺寸),此时人工表面等离激元波导成为具有周期调制的非均匀传输线,人工表面等离激元将转换为漏波辐射到自由空间。同时,随着周期进一步增大,-1阶、-2阶、-3阶等高阶空间谐波将逐个转换为漏波,从而产生多波束辐射,形成多波束漏波天线。本文揭示了SSPP波导调制周期尺寸大小对其电磁特性调控的一般性理论,所设计的漏波天线在点对多点通信系统和微波集成电路中有巨大的发展前景。

1.3 全波仿真结果

2 漏波天线的设计
2.1 仿真结果

2.2 实验验证

3 结束语
