体验随机性 量化可能性
2022-04-20潘锦嫦
摘 要:基于单元整体教学理念,文章对“可能性”单元原教材内容进行调整,以求学生更好地体验随机性,量化可能性,进而形成数据分析观念。第一课时是新知学习,教师组织活动,结合具体情境,让学生感受随机性现象;第二课时是实践探究,汇总数据,揭示内在联系,沟通概率与统计知识;第三课时是实践体验,设计转盘,结合理论分析,引导学生量化可能性大小。
关键词:随机性;可能性;单元教学;数据分析观念
中图分类号:G427 文献标识码:A 文章编号:2095-9192(2022)11-0082-03
引 言
“统计与概率”是小学数学课程学习内容之一,但一直以来有关统计的内容基本与随机性无关,小学阶段也没有出现关于概率的定义。《义务教育数学课程标准(2011版)》(以下简称《课程标准》)将“统计观念”表述改为“数据分析观念”,增补了“体验随机性”的学习要求,并对“随机现象发生的可能性”进行了具体的描述:在具体情境中,通过实例感受简单的随机现象,能列出简单的随机现象中所有可能发生的结果;通过试验、游戏等活动,感受随机现象发生的可能性是有大小的,能对一些简单的随机现象发生的可能性大小作出定性描述与交流[1]。关于可能性的学习,人教版数学五年级(上册)教材中并没有直接出现概率的定义,而是用可能性来引导学生初步学习概率的知识,概率称为“随机现象发生的可能性”,主要教学事件的确定性和不确定性,教学重点是让学生通过实例感受简单的随机现象,能列出简单的随机现象中所有可能发生的结果,并对一些简单的随机现象发生的可能性大小作出定性描述,运用概率的思想方法来解释日常生活中的随机现象。五年级学生处于具体运算阶段(7~12岁),能够区分确定和不确定,知道如何量化概率,在计算复杂事件的概率时拥有一套不完整的对策[2]。
学生有足够的生活经验,对可能性知识的理解没有太大的困难。如何在学生朴素的生活经验中渗透统计与概率思想,形成数据分析观念是本单元教学的重难点。
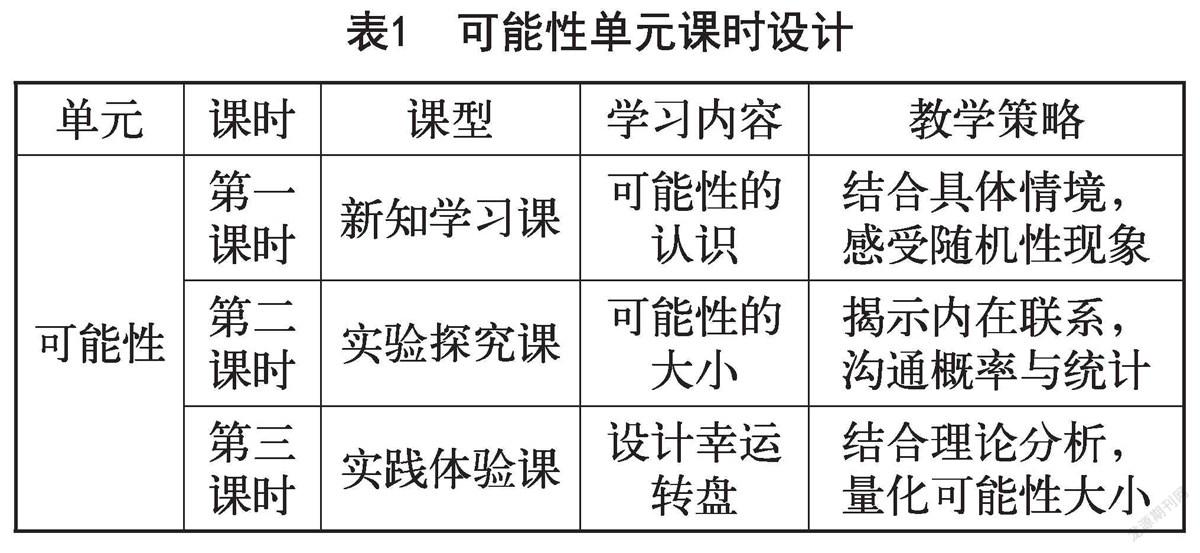
以单元为整体进行教学设计,是挖掘数学本质、整体把握知识结构、渗透数学价值、发展学生数学学科核心素养最有效的途径[3]。笔者统整“可能性”单元教学目标,将单元整体分析概括为以下四点:一是生活中的现象可以用数学语言来准确描述;二是在随机现象中感受对同样的事件每次收集到的数据可能不同,但有足够的数据就可能从中发现规律;三是数据分析观念是数学学科核心素养之一,通过收集和分析数据可以对数据中所蕴含的信息做出理性判断;四是了解“猜想—验证”是数学研究的常用方法。基于原教材内容进行调整(见表1),笔者尝试开展单元整体教学,并分享单元教学策略。
一、新知学习:结合具体情境,感受随机性现象
《课程标准》明确指出关于“概率”的教学重点是学习感受随机性。从数学的角度出发,生活和自然中的现象可以分为确定现象、随机现象和模糊现象[4]。确定是必然,也就是结果一定。随机现象和模糊现象都是不确定的,随机现象是结果不确定,而模糊现象是事物本身的定义不确定,这需要教师帮助学生准确区分。
为帮助学生理解区分这三种现象,在第一课时中,笔者设计了如下两项活动。首先是“抽牌体验”,让学生初步感受事件发生的确定性和不确定性。从三张卡片(1、2、3)中抽得分数高者获胜:第一次意在熟悉规则,通过 “你想抽到什么”和“想抽到就一定能抽到吗”两个问题帮助学生区分主观意愿与客观实际;第二次重在感受随机,通过提问“这次抽到的牌和上次一样吗”,把两次抽取卡片的结果进行对比,让学生明白相同条件下,抽取的结果也不一定相同;第三次初步体验可能、不可能、一定,有三张牌 “可能会抽到什么”,“1”“2”“3”都有可能,初步感受简单随机事件中所有可能发生的结果是有限的。也就是说,抽取一张(假设1),剩下两张,“现在可能会抽到什么?还可能抽到1吗”?已经抽了就不可能再抽到;再抽取一张(假设2)只剩一张,“你能确定是几吗”?学生明确一定是3,初步感受事件发生的确定性和不确定性,确定包括一定和不可能,不确定则是可能。其次是“抽球活动”,从三个不同的装球箱中抽到红球者获胜。第一个箱子中全是白球,学生多次抽取发现不管怎么抽都是白色,从而猜测箱子中全是白球,总结出“只有则一定”;第二个箱子中有各种颜色的球,但沒有红球,学生多次抽取发现不管怎么抽都没有抽到红球,从而猜测箱子中没有红球,总结出“没有则不可能”;第三个箱子中按照学生的要求放入红球,总结出“有则有可能”。
学生亲身经历概念形成的全过程,从而真正体会随机的概念,深入理解“一定”“不可能”“可能”的含义,感受事件发生的确定性和不确定性。教师通过“生活中的数学”,让学生进一步区分生活中的模糊现象与数学中的随机现象,学以致用,用数学语言“可能”“一定”“不可能”描述生活中事件发生的可能性,体会数学与生活的密切联系。
二、实验探究:揭示内在联系,沟通概率与统计
使用概率方法的统计学被称为推断统计学,统计与概率的融合有助于帮助学生认识二者的关系,将知识融会贯通,系统掌握[5]。教材中设置大量的实验,依靠学生自己摸索,用经验性活动得来的频率进行验证,而往往由于试验的次数过少,得到的结果常与分析的可能性结果不相符,学生在试验后反而糊涂。利用数据分析感受概率,是教学的核心,能有效解决这一问题。
为帮助学生在数据统计中加深对可能性的理解,在第二课时的教学中,笔者设计如下两项实验。首先是通过抽扑克进行的“等可能性”实验,教师给每个学生准备方块、梅花、桃心和黑桃四种花色的扑克牌各一张,反面朝上,打乱顺序,让学生任意抽出一张。以举手方式统计抽到各种花色的次数,教师在电脑上进行记录。再把牌放回去,洗牌抽下一张,连续抽10次。每填入一次数据,电脑自动统计抽到不同花色扑克的总次数。在这一过程中,学生直观感受自己每次抽到的花色不一定相同,体验随机性;同时在多次的数据汇总中,惊奇地发现随着数据的累加,四张花色卡片抽到的总次数呈现接近的趋势,体会到有足够的数据就可能从中发现规律。教师追问:“如果抽取的次数更多,你猜结果会如何?”学生回答:“越来越接近,但不一定相等。”从而理清理论概率和实验频率的区别。其次是进行数量不等的“分组抽球”实验。箱子中放有红、黄两种颜色的球若干个(如红球1个,黄球4个),每次抽取一个再放回,连续抽取20次并记录产生的数据,小组内明确分工,谁负责摸球、谁负责记录、谁负责监督等,以保证数据的有效性。小组实验后,教师对各组数据进行收集汇总,并引导学生对结果进行观察:“每一个小组的统计结果都一样吗?”学生可以看出每个小组抽球的结果有的相同,有的不相同,甚至可能出现抽到红球的次数比黄球多的情况。学生根据统计结果推断箱子中红球的数量比黄球少。教师提问:“箱子里一共有5个球,猜一猜红球和黄球各有多少个?”引导学生根据汇总结果进一步猜测。教师要鼓励学生得出多种答案,只要能根据数据进行合理推断即可。最后,教师开箱验证,并回顾特殊数据,引导学生认识不确定性的普遍存在,用数据分析可能性的同时承认例外,发生的可能性再小也依然有可能发生。
通过两项实验,学生知道事件发生的可能性大小与物体的数量有关,初步感受随机现象的统计规律性。根据实际情况合理推测可能性大小,根据试验的数据推测产生结果的原因,帮助学生认识到足够多的数据中蕴含着统计规律,逐步形成统计观念,进而形成尊重事实、用数据说话的态度和科学的世界观与方法论。
三、实践体验:重视理论分析,量化可能性大小
用一个数来描述某种事件发生可能性的大小,称这个数为该事件发生的概率。张奠宙指出:“在小学阶段,必须直面‘概率’概念,把随机性的数学直觉‘概率化’。”[6]而教材中只有“可能性”大小的讨论,没有给“可能性”赋予数值。对五年级的学生来说,用分数表示可能性的大小并不困难。
在第三课时教学中,笔者创设给商场设计“幸运大转盘”的情境,首先出示一个平均分成8份的转盘范例,其中1份为红色、2份为黄色、5份为蓝色,让学生对转盘有整体的认识。教师要引导学生运用可能性大小的知识分析“转到哪种颜色的可能性大?哪种颜色的可能性小?”并说明理由,从而检验学生对可能性大小的掌握情况。然后让学生尝试用分数表示转到各种颜色的可能性是多少(如红色占了8份中的1份,可以用分數表示),初步感受可能性的大小不仅与数量有关,还可以进一步量化,用具体的数值来表示,便于比较大小并由此推测各种颜色分别表示什么奖项。其次是小组合作设计“幸运大转盘”。教师为每个小组提供等分12份的圆形转盘和三种不同颜色的笔,统一规定红黄蓝分别表示一二三等奖,要求各小组设计转盘并用分数表示出各个奖项的可能性大小。任务完成后,教师组织班级进行交流分享,让各小组展示设计的转盘并讲述设计原因。教师在判断各量化可能性大小的分数结果是否正确后,对各小组的作品进行比较分析,引导学生围绕“如果你是商家,你会选择哪组设计的转盘?”“如果你是顾客,你选择用哪个转盘来抽奖?”两个角度进行思考,运用可能性大小的赋值来分析说理,做到有理有据。最后分组进行转盘抽奖体验,让学生在数据的统计分析中感受量化的可能性大小只是一个理论数值,进一步理清理论概率和实验频率的区别。该活动中采用的转盘呈现的是几何概率,因其具有直观性而容易被学生接受,使学生根据分数的定义给“可能性”赋予数值。量化可能性的大小可以帮助学生更好地理解不同事件可能性的大小会有所不同,但一定在0到1之间,学会运用概率的思想方法来解析日常生活中大量的随机现象,为日后概率的学习做好铺垫。
在单元学习后,教材还安排了“掷一掷”的综合实践活动,让学生综合运用所学知识解决问题,培养学生猜想、试验、分析、验证和解决问题的能力,进一步体会事件发生结果的可能性有大有小;透过偶然发现必然,判断哪些结果出现的可能性大,哪些结果出现的可能性小。而学生通过量化可能性的大小,在分析中利用概率梳理说明可能性的大小,能使判断更有依据、更为科学、更具说服力。
结 语
文章结合笔者的教学实践,围绕“可能性”开展大单元教学,对单元教学内容进行整体分析和重组,落实各课时教学设计并提出相应的教学策略。在数学活动中认识和理解可能性,不能只是让学生记住法则,更重要的是使其亲身经历法则形成的全过程,从而进行深入思考,这样才能把体验转化为对可能性的理解,体验随机性,量化可能性,在扎实了解统计“双基”的同时,将其升华为数据分析观念,促进学生数学学科核心素养的形成与发展。
[参考文献]
[1]中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]张增杰,刘范,赵淑文,等.5~15岁儿童掌握概率概念的实验研究:儿童认知发展研究(Ⅱ)[J].心理科学通讯,1985(06):3-8,66.
[3]侯学萍,陈琳.小学数学单元教学的整体设计[J].教学与管理,2018(29):43-45.
[4]李明亮,曾鹏,杨梦霞.新课程标准下小学概率教学探究[J].湖南第一师范学院学报,2014,14(01):27-30.
[5]蒋秋,陈朝东.小学数学教科书中“统计”与“概率”内容的融合探析[J].教育导刊,2013(10):67-70.
[6]张奠宙,巩子坤,任敏龙,等.小学数学教材中的大道理:核心概念的理解与呈现[M].上海:上海教育出版社,2018.
作者简介:潘锦嫦(1983.3-),女,广东中山人,任教于中山市西区烟洲小学,中山西区中心教研组组长,小学一级教师,硕士学位,中山市小学数学骨干教师。
