巧借例习题拓展提升数学应用能力

孙静

[摘  要] 在高中数学习例题教学中，大多数教师习惯于讲新题，认为唯有新题才能激发学生探究的热情，因而忽视了对例习题的再利用，将学生引入茫茫题海. 实际上，教材中的例习题富含深意，若将其仔细推敲和拓展不仅可以发现问题中的一般规律，而且能找到解决问题的通法，有利于减轻学生的课业负担，提高习题教学的质量. 为此，教师应重视例习题的拓展，通过变式拓展、解法拓展、结论拓展等提升学生解决问题的能力.

[关键词] 例习题;拓展;解决问题

教材是开展一切教学活动的重要依据，是学生学习的源头活水，凝聚着编写者的智慧，蕴含着丰富的内涵，其在数学教学中的作用是不言而喻的，然现实教学中却常常出现“轻教材重题海”的现象，部分教师认为教材的概念、公式、定理等经过了无数次验证，会背能应用就可以了;另外，教材中的例习题也较浅显，没有课外例习题那样灵活生动，故容易将学生推进茫茫“题海”. 殊不知，这样不仅会增加学生的课业负担，而且容易出现思维定式，解题时常“知其然而不知所以然”. 久而久之，学习成绩不升反降，学生的学习能力未能获得明显提升. 为此，在教学中，教师必须认真研读教材，领会编写者的真正意图，通过对教材内容的拓展和延伸领悟蕴含其中的数学思想和问题本质，进而有针对性地应用适合的教学手段让学生领悟解题方法和解题技巧，借此達到减负增效的效果.

从教学实践反馈来看，教材例习题的利用率较低，大多仅应用于新授课阶段，在复习阶段应用甚少，若能对其深入探究，不仅可以加深对基础知识的理解，而且有助于旧知的巩固和新知的内化;另外，从学生熟悉的内容出发进行再探究也容易激发学生的兴趣，增加学习信心. 为此，在数学教学中，教师要重视例习题的挖掘和拓展，以此提高数学教学实效，促进学生学习能力提升. 那么应如何拓展例习题呢？笔者选取了几个典型案例进行剖析，以期通过例习题拓展为学生减负增效.

[⇩] 变式拓展，活学活用

有些例习题看似平淡无奇，然深入探究却可以发现其中隐藏的一般规律，为了引导学生发现这些规律，教师在教学中可以安排一些变式拓展，这样不仅可以提升学生的解题兴趣，而且可以深化知识的理解和应用，促进学生学会发现、学会总结、学会创新.

例1 在△ABC中，B（-6，0），C（6，0），直线AB，AC的斜率乘积为，求顶点A的轨迹.

分析：本题若直接从求解的角度进行分析并不难，设A的坐标为（x，y），根据各点的坐标可以直接表示出直线的斜率，再利用“直线AB，AC的斜率乘积为”得出等式，化简等式后可得顶点A的轨迹方程为-=1（x≠±6）. 若本题仅限于探究简单的顶点A的轨迹，其价值难以体现. 为此，在此基础上尝试通过变式进行拓展和延伸，有利于揭示其中隐藏的秘密.

变式：在△ABC中，B（-6，0），C（6，0），直线AB，AC的斜率乘积为-，求顶点A的轨迹.

利用例1的解题思路可以直接得到顶点A的轨迹方程为+=1（x≠±6）.

在例1中发现=，在变式中发现 -=-，那这是因为斜率乘积值比较特殊才出现了这种效果还是本身就有这样的一般规律呢？显然通过简单的变式拓展激起了学生探究的热情.

探究过程：在推导椭圆标准方程时有（a2-c2）x2+a2y2=a2（a2-c2）这个式子，移项整理得a2y2=（a2-x2）（a2-c2），当a2≠x2时，有=，即·=-. 由代数式的几何意义可以得出如下结论：

结论1：椭圆+=1（a>b>0）的长轴两顶点A（-a，0），B（a，0）与椭圆上任意一点P（x，y）（除长轴两顶点外）的连线的斜率之积为定值，即k·k=-;双曲线-=1（a>b>0）的实轴两顶点A（-a，0），B（a，0）与双曲线上任意一点P（x，y）（除实轴两顶点外）的连线的斜率之积为定值，即k·k=.

结论2：E，F，P是椭圆+=1（a>b>0）或双曲线-=1（a>b>0）上相异的三个点，O为坐标原点，若E，F，O三点共线，则直线PE，PF的斜率之积为定值 -或.

结论2的证明较简单，这里就不再详细阐述，只要根据E，F，O三点共线，可设E（m，n），F（-m，-n），再设点P的坐标为（x，y），通过斜率相乘并化简即可得结论2.那么在此大张旗鼓地进行变式拓展，是否有其真正的应用价值呢？现以一道高考题目为例，带领学生体验该结论的应用价值.

例2 已知点P（x，y）（x≠±a）是双曲线E：-=1（a>b>0）上一点，M，N分别是双曲线E的左、右顶点. 若直线PM，PN的斜率之积为，求双曲线E的离心率.

例3 已知椭圆+=1（a>b>0）的左、右顶点分别为A，B，点P在椭圆上且异于A，B两点，O为原点. 若直线AP，BP的斜率之积为-，求椭圆的离心率.

例2和例3为两道高考真题，因为有之前拓展的经验，因此问题可以迎刃而解. 若之前没有实施变式拓展，学生求解时势必会花费大量的时间，不利于高考解题效率的提升. 为此，对例习题的变式拓展有利于学生抓住问题的本质特征，找到问题的一般规律，进而实现深入理解、灵活应用的目的.

[⇩] 结论拓展，深化运用

教材中有些例习题的解法、结构、问题背景是类似的，因此在教学时将这些相似的题目进行类比，借助于“多题一讲”，深挖题目的内涵和外延，抽象出问题的本质特征，这样不仅可以将学生从题海中解放出来，而且可以抓住问题的本质，解题时往往会收到意外惊喜.

例4 （1）设a>0，b>0，求证a3+b3≥a2b+ab2.

（2）设a≠b，求证a4+b4≥a3b+ab3.

（3）若a，b均为正数，求证a5+b5≥a3b2+a2b3.

例4中的三道题是高中数学教材中的三道选修题，大多数教师都感觉证明过程简单没有必要花大篇幅学习，只要会证明就可以了. 殊不知，这不屑一顾的小题目中竟然隐藏着大秘密. 显然，由这三道题进一步推广可以得出这样的结论：若a，b均为正数，m，n∈N，则am+n+bm+n≥ambn+anbm.

证明：am+n+bm+n-ambn-anbm=（am-bm）·（an-bn）. ①当a=b时，am+n+bm+n=ambn+anbm;②当a≠b时，am-bm与an-bn的符号相同，所以（am-bm）（an-bn）>0，即am+n+bm+n>ambn+anbm. 由①②可得am+n+bm+n≥ambn+anbm（当且仅当a=b时等号成立）.

例5 设a，b为非负实数，求证a3+b3≥（a2+b2）.

证明：a3+b3-（a2+b2）=a2·（-）+b2（-）=（-）[（）5-（）5]=（-）2[（）4+（）3（）+（）2（）2+（）（）3+（）4]≥0，即a3+b3≥（a2+b2）.

例5是高考真题，虽然得以正确求解，然其计算过程复杂，若运用推广得到的结论，两边平方可得a6+b6≥a5b+ab5，这样求解问题就显得更容易了. 根据学生反馈可知，本题很多学生因运算过程复杂而未能正确证明. 考试后，有些教师也尝试应用构造函数的思路进行证明，然都没有以上结论的应用显得简洁明了. 因此，教材中无处不是宝贵的财富，在复习教学中一定要重视教材回归，这有利于学生对知识的深化理解，有利于解题效率的提升.

[⇩] 解法拓展，深化理解

学生做课后习题时常习惯于套用例题的解决思路，很多习题确实是例题的变式，应用例题的解决思路往往可以轻松解答习题，进而实现巩固知识的目的;然数学题目灵活多变，有时单一套用例题的解决思路很难实现数学能力的提升. 因此，在平时练习时可以引导学生从不同角度进行分析，这样往往可以收获不同的解题方法. 当然，也许在此过程中可能碰壁，然通过多角度分析可以使学生的思维更广阔，使学生对知识的理解更深刻.

例6 如图1所示，ABDC是梯形，其中AB=a，CD=b，连接AD，BC交于点O，过点O作EF∥AB. GH是梯形的中位线，KL平行于两底且使梯形ABLK与梯形KLDC相似，MN平行于两底且使梯形ABNM与梯形MNCD的面积相等. 试研究线段GH，KL，EF，MN与代数式，，，之间的关系，比较它们之间的大小关系并利用基本不等式加以证明.

分析：由題意可求出GH=，KL=，EF=，MN=. 由图1可知，MN>GH>KL>EF，所以>>>.

用基本不等式证明：因为a，b为不相等的正数，所以>>0，所以<，所以<，即<.

又-

==>0，所以>

，即>.

综上，利用梯形模型和基本不等式证明了这个“不等式链”. 那么是否存在其他的证明方法呢？接下来，教师可以引导学生结合已学的半圆模型进行证明.

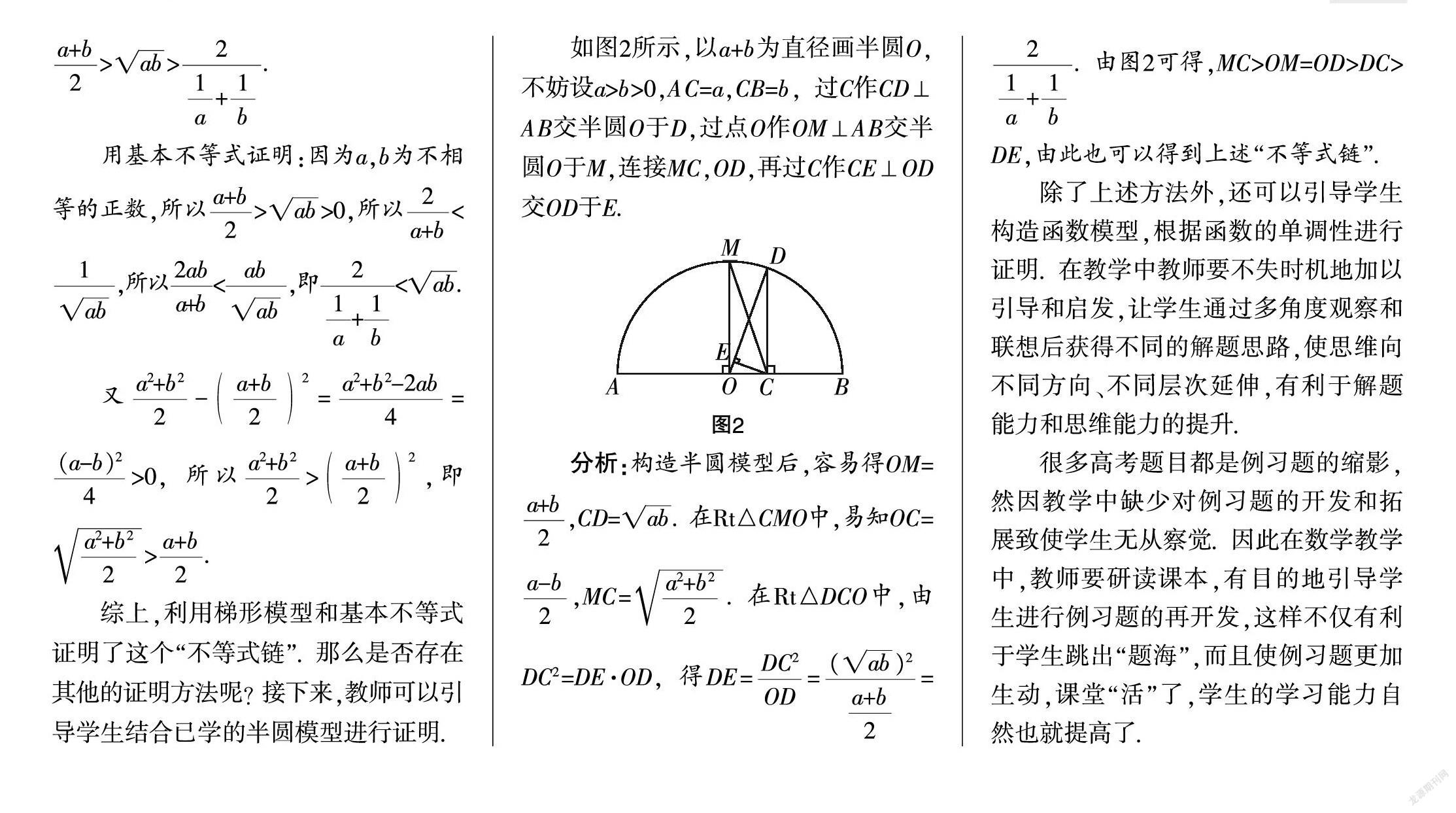
如图2所示，以a+b为直径画半圆O，不妨设a>b>0，AC=a，CB=b，过C作CD⊥AB交半圆O于D，过点O作OM⊥AB交半圆O于M，连接MC，OD，再过C作CE⊥OD交OD于E.

分析：构造半圆模型后，容易得OM=，CD=. 在Rt△CMO中，易知OC=，MC=. 在Rt△DCO中，由DC2=DE·OD，得DE===. 由图2可得，MC>OM=OD>DC>DE，由此也可以得到上述“不等式链”.

除了上述方法外，还可以引导学生构造函数模型，根据函数的单调性进行证明. 在教学中教师要不失时机地加以引导和启发，让学生通过多角度观察和联想后获得不同的解题思路，使思维向不同方向、不同层次延伸，有利于解题能力和思维能力的提升.

很多高考题目都是例习题的缩影，然因教学中缺少对例习题的开发和拓展致使学生无从察觉. 因此在数学教学中，教师要研读课本，有目的地引导学生进行例习题的再开发，这样不仅有利于学生跳出“题海”，而且使例习题更加生动，课堂“活”了，学生的学习能力自然也就提高了.