对矩形波导中电型并矢格林函数表达式中奇异项的讨论
2022-04-19雒向东赵宇杰
雒向东,张 明,海 波,赵宇杰
(1.兰州城市学院 电子工程学院;2.甘肃高师 学报编辑部;3.兰州城市学院 信息工程学院,甘肃 兰州 730070)
1 问题的提出
一个并矢格林函数以场源来表示场,即将场看成是点源的场的组合.并矢格林函数可按照在某一表面上或者在经过不连续面时所满足的边界条件进行分类,可分为第一、二类电型和第一、二类磁型以及第三类并矢格林函数.汉森在解决某些电磁问题时,首先引进了三类矢量波函数,分别以L、M、N表示,它们都是齐次亥姆霍兹矢量方程的解.为了推导磁型并矢格林函数本征函数展开式,戴振铎在他的著作中指出不需要使用L函数,[2]但如果要导出电型并矢格林函数本征函数展开式,就必须使用L矢量波函数.曾广侃在他的论文中直接导出了电场和磁场所满足矢量波动方程的电型并矢格林函数表达式为:[3]
(1)

2 电型并矢格林函数的两种推证方法
2.1 磁型格林函数推导方法[4-5]
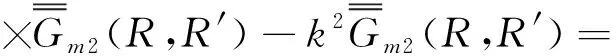
(2)




(3)
用函数Nem′n′(-h′)做上式前标积,用正交关系和归一化系数公式解出系数为
(4)
(5)
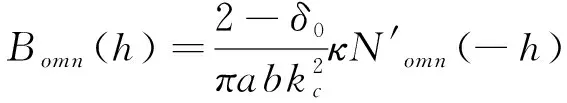
(6)


(7)

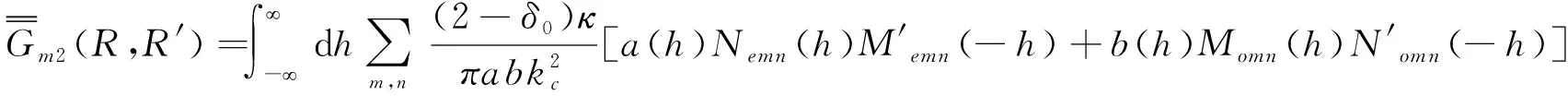
(8)
将(7)和(8)两式代入(2)式得
(9)
(10)
(11)

在z=z′处函数不连续,不连续磁型并矢格林函数边界条件为
(12)
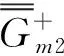
(13)
(14)
由广义函数理论知

(15)
利用以上关系可推得
(16)
2.2 电型格林函数推导方法[4-5]

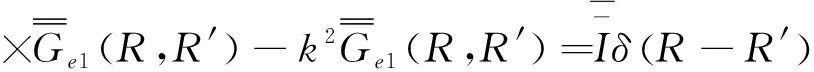
(17)
引入矢量波函数Lomn,Lomn(h)定义为
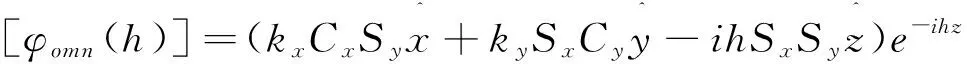
(18)

(19)
Sx=sinkxx,Cx=coskxx,Sy=sinkyy,Cy=coskyy
(20)
Lomn(h)函数本身以及与其它两组函数正交关系如下
(21)
(22)
(23)
可以看出Lomn(h)、Nomn(-h′)在空域包括h的域内是正交的,正交关系表示如下
(24)
根据欧姆—瑞利方法,假设
(25)
为了确定三个系数A、B、C,用Lom′n′(-h′)对(25)式作前标积得
(26)
用Mem′n′(-h′)、Nom′n′(-h′)对(25)式分别作前标积同样可得
(27)
(28)
(29)

(30)

(31)
略去“mn”下标,把(30)和(31)式代入(17)式得
(32)

(33)
把Lo和No分成两部分Lo=Lot+Loz,No=Not+Noz
(34)
Lot和Not代表横向分量,Loz和Noz代表纵向z分量,这样可推得(33)式为
(35)
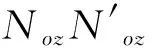
(36)
(37)

(38)
(39)
(40)
结果同(16)式.
3 电型并矢格林函数表达式中奇异项的讨论

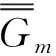
(41)
(42)
(43)
(44)
(45)

(46)

如果波导内有一电流J(R′),无旋电场可由下式计算:[7]
(47)
若将空间电荷场暂且记为Es,依据电磁理论基本关系

(48)
φomn(h)为标量本征函数,对(48)式应用格林函数法求解可得[9]
(49)
从φomn(h)和J(R′)的边界条件可以证明下式

(50)
将(50)代入(49)式并对φ取梯度得

(51)
证明得Es(R)=El(R)
(52)

4 关于L类矢量波函数的说明

∇×∇×M-κ2M=0
(53)
所以它是电磁场方程在无源时的解,可称为场的本征模式,具有明确的物理意义.而L满足方程
∇·∇L+κ2L=0
(54)
总 结

