面向缺失数据的布鲁姆近似成员查询算法*

吴佳雯 ，王宇科 ，裴书玉 ，谢 鲲 ，刘楚达

(1.湖南大学 信息科学与工程学院，湖南 长沙 410082；2.湖南大学 校园信息化建设与管理办公室，湖南 长沙 410082；3.长沙航空职业技术学院，湖南 长沙 410082)

0 引言

标准的布鲁姆过滤器(Bloom Filter，BF)[1]是一个空间效率很高的数据结构，它可以表示集合并支持集合的成员查询，快速判断查询元素是否在集合中。当给定一个查询元素e 时，它被用来回答查询元素是否在这个集合。一个标准的布鲁姆构造一个长度为m 的比特位数组，初始化为0。在插入阶段，它使用k 个独立的哈希函数h1(·)，…，hk(·)来计算插入元素在数组中对应的k 个哈希位置h1(e)%m，…，hk(e)%m，并将这k 个哈希位置置位为“1”。在查询阶段，通过检查是否所有的k 个哈希位置都置位为“1”，来判断元素是否在集合中。如果它们都置位为“1”，则认为查询元素e 在集合S 中；否则，则认为查询元素e 不在集合S 中。

现有标准布鲁姆过滤器通常用于常规的精确匹配的成员集合查询(Exact-matching Membership Query，EMQ)，即：检查查询数据本身是否存储在布鲁姆过滤器，它是否是集合的一个成员。布鲁姆过滤器作为一种空间精简、查询高效的支持成员集合查询结构，一直被广泛用于各种实际应用中[2-3]。在网络领域应用中，布鲁姆过滤器可以用来存储防火墙海量的黑名单数据[4]，以及在网站中进行内容去重等[5]。在大数据应用中，例如HBase 中使用布鲁姆过滤器来减少代价高昂的I/O 次数，提升数据库查询效率[6]。

然而，在新兴的网络应用中，传统的布鲁姆过滤器所提供的精确匹配已不足以应对各种各样的网络应用需求。这些应用要求现有算法可以对数据进行近似成员查询(Approximate Membership Query，AMQ)[7]。与精确匹配不同的是，如果AMQ 返回肯定的结果，那么这里存在两种情况：第一是查询元素本身存在于BF 中，第二是查询元素本身在某个范围内与BF 中存储的一条或多条元素近似。AMQ 是给定距离度量下，考察查询数据与集合S 中任意成员的接近程度。这个距离的度量可以是汉明距离(Hamming distance)[8]、欧氏距离(Euclidean distance)[9]等。AMQ 常常应用在各种领域，如信息中心网络(Information-Centric Networking，ICN)[10-12]利用AMQ 来进行IP路由选择，在图像检索领域使用AMQ 进行相似图像检索等。

近些年来针对AMQ 的布鲁姆过滤器研究得到了学术界越来越多的关注[7，13-15]。Kirsch 等人最先将局部敏感哈希函数(Locality-Sensitive Hashing，LSH)[15]和BF 结合，提出距离敏感的布鲁姆近似查询算法(Distance-Sensitive Bloom Filters，DSBF)[9]。在DSBF 基础上，Qian Jiangbo 等人提出了一种汉明多粒度局部敏感布鲁姆过滤器(Hamming Metric Multi-Granularity Locality-Sensitive Bloom Filter，HLBF)[7]，HLBF 支持不同粒度汉明距离的近似成员查找。

然而这些支持近似成员查询的布鲁姆过滤器结构都有一个共同的局限性。存储和查询元素必须是完整的数据，无法处理请求查询含有缺失数据的情况。现实生活中的数据集合并不是完整无缺的，它们元素通常为高维空间的元素，高维数据往往还伴随着维度冗余的情况，且存在数据缺失。

为了解决这个问题，本文提出一种面向缺失数据的布鲁姆近似查询算法。它先对缺失数据进行预填充，再通过PCA(Principal Component Analysis，PCA)算法[16]将高维数据转换到低维数据，使用低维数据进行布鲁姆的近似查询。在近似查询中，采用局部敏感哈希函数与标准哈希函数结合的方式来插入、查询低维数据。本文使用局部敏感哈希函数中AND 和OR 操作相结合的方法进一步降低算法的假阳性率与假阴性率，提高了算法的性能。本文在真实数据集上对所提算法进行了验证，充分证明所提算法有效地解决了存在缺失数据的情况下近似成员的查询问题。

1 方案概述

本文设计一个新颖的布鲁姆结构，用来实现面向高维缺失数据的近似成员查询。近似成员查询指的是，当查询元素与现有集合中的某些元素在某个范围内相似时，该查询元素就被视为集合的一个近似成员。本文给出近似成员查询的基本定义如下：

定义1(近似成员查询)给定一个距离参数R、元素集合S，查询元素q 被视为近似于集合S，当且仅当：∃p∈S，||q，p||≤R，其中，||*||表示q 与p 之间 的距离，距离的度量方式可以是汉明距离、欧氏距离等。当R=0时，该查询就是一个精确的成员查询，因此精确查询可视为是一个特殊的近似查询。

设计的面向缺失数据的布鲁姆近似查询算法的方案如图1 所示，主要分为3 个步骤：

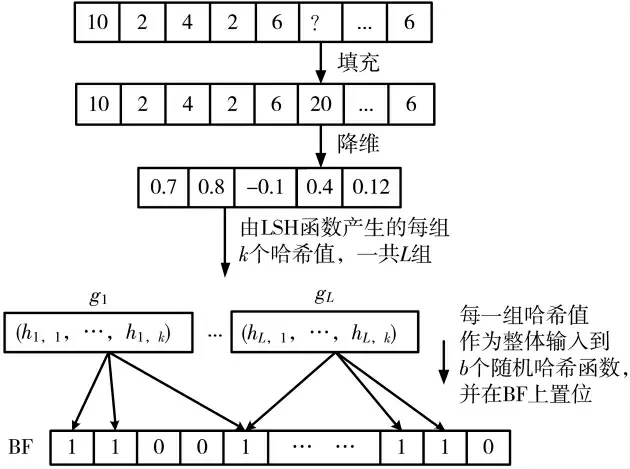
图1 面向缺失数据的布鲁姆近似成员查询方案

(1)填充高维的缺失数据。缺失的原始数据无法直接在布鲁姆过滤器中存储/查询，需要对缺失的数据进行填充；

(2)基于PCA 技术，将高维填充数据降维表示到低维空间，去除不相关属性，提取出数据的重要特征；

(3)在插入阶段，利用LSH 哈希函数族为降维后数据生成L 个独立的组，每一组看作是原数据的哈希值表示。并将每一组作为一个整体输入，再通过b个传统随机哈希函数进行哈希运算，对映射在BF 上的哈希位置置位为“1”，完成低维数据在布鲁姆过滤器的存储。

2 详细设计

2.1 缺失数据预填充与PCA 降维

由于原数据带有缺失，而使用PCA 降维[16]的数据需要维度对齐，因此需处理数据的缺失处。

具体地，首先计算出原始数据每个维度无缺失处的均值，记录下各个维度的均值，并使用维度均值补全缺失处的值，以上即为对数据的初步处理操作。

接着，将处理后的数据组织成一个n×d 的矩阵X，X中每行代表一条数值向量，每列代表一个维度。并使用标准的PCA 降维技术：矩阵去中心化X—协方差矩阵计算—选取投影矩阵P—降维计算×P，至此，完成了缺失数据的预处理和降维操作。

2.2 插入算法

在PCA 降维后，使用降维后的数据作为下一阶段的输入数据进行插入操作，具体地：

(1)利用p-stable LSH[9]得到L 个哈希值的集合，哈希函数为h(a，e)=(a·v+e)/w」，其中v 为输入数据，a 为与v 维度相同的一个随机向量，a 中的每个分量均从p-stable 分布中获取，w 为桶宽，e 是一个大于等于0且不大于w 的随机数。本文在高斯分布中选取a 的值，通过变换a 和e 的取值得到一个大小为k 个的哈希值集合：

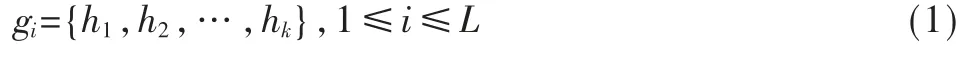
其中，hj(1≤j≤k)表示利用p-stable LSH 得到的第j 个哈希值，一个gi组包含k 个哈希值，gi(1≤i≤L)表示第i组哈希值集合，重复上述生成一个组的步骤，一共生成L 个组。

(2)将每个gi组作为输入，使用b 个独立的随机哈希函数将其映射到布鲁姆过滤器的b 个位置。具体地，一个标准的随机哈希函数将一个gi组映射为一个值，然后将该值模上位数组大小得到一个数值，这个数值即为插入的位置。此步骤可表示为：

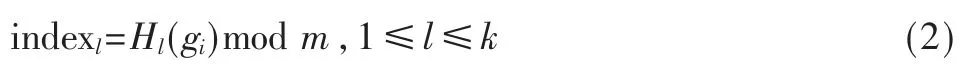
其中，Hl(*)表示第l 个标准的随机哈希函数，m 表示位数组大小，indexl表示使用第l 个哈希函数定位到的位置，然后将位数组中第indexl位的值置为1。重复上述第二阶段，使得L 组gi都被映射到布鲁姆过滤器位数组中，这样就完成了一次插入操作。综上所述，对于每一条输入数据，位数组中共有L×b 个位置被置为“1”。

2.3 查询算法

布鲁姆过滤器的查询操作一般发生在插入操作完成之后。带有缺失的查询数据在使用近似查询布鲁姆过滤器进行近似查询之前，同样需要对数据进行预填充和PCA 降维处理。使用降维后的数据作为输入数据在布鲁姆中查询，具体地：

(1)与插入算法的第一步相同，使用p-stable LSH 函数得到L 组哈希值集合{g1，…，gL}，其中每一组gi包含k 个哈希值，即：gi={h1，h2，…，hk}。相似查询中，相近 的值可能会落于相邻的桶中，因此与插入操作不同是，除了每一组gi，还需要扩展每一组哈希值集合gi为2k 组哈希值集合，作为下一步随机哈希函数的输入。

(2)将每一组gi和由它扩展的2k 组哈希值集合(1≤j≤2k)，一共作2k+1 组哈希函数集合，作为随机哈希函数输入。计算每一组哈希函数映射到布鲁姆的b 个位置，判断b 个位置是否全部被置为“1”。

如图2 所示，将每一组gi扩展成2k 组哈希值集合的方式是：对于组中{h，h，…，h}每一个哈希值，将其12k值减1 而其他值保持不变得到一组哈希值集合，然后将其值加1 而其他值保持不变得到另一组哈希值集合，这样原来的一组哈希值集合gi就扩展成了2k 组哈希值集合，1≤j≤2k，即：

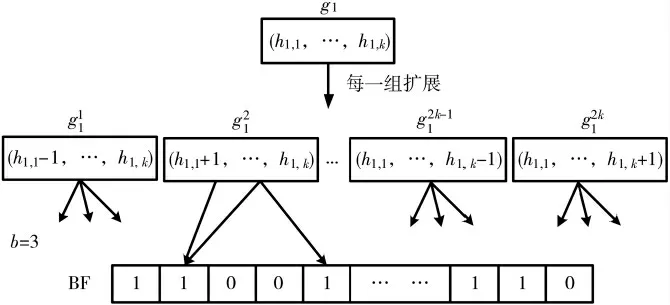
图2 近似成员查询操作

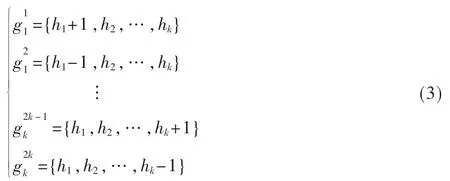
对于每组哈希值集合gi和它对扩展的2k 组哈希值集合，若任意一组在BF 的b 个索引位置都被置为1，则查询元素存在。否则，查询数据与给定集合并不相似。

2.4 假阳性分析

假阳性率出现在原数据不与插入到布鲁姆过滤器中的集合近似，但是查询结果返回true 的时候，也就是说算法误认为在插入集合中存在与查询数据相近的数据。因此，假阳性误判率由两个部分组成：局部敏感哈希产生的假阳性误判率、标准哈希函数产生的假阳性误判率，因此假阳性率可表示为：

其中，PLSH表示由局部敏感哈希产生的假阳性误判率，FPRSBF表示由带有b 个哈希函数的标准布鲁姆过滤器产生的误判率。

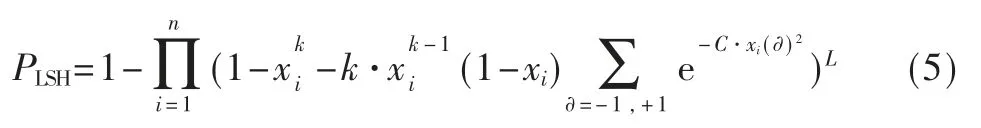
其中，L 表示组数，k 表示每组包含的哈希值个数，n 表示插入到布鲁姆过滤器中数据的个数，C 是常量，x(∂)可表示为：

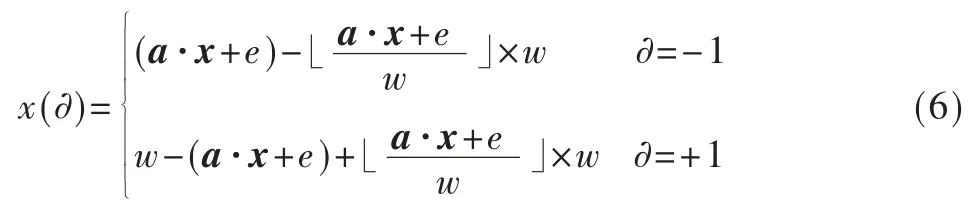
其中，a 是和原数据维度相同的随机向量，w 表示桶宽，e为[0，w]范围内的随机数。

又由[7]可知，在标准的BF，其假阳性误判率为：

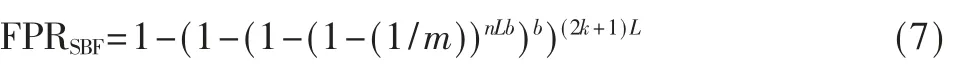
其中，m 表示位数组大小，b 表示使用的标准哈希函数个数，k 表示每组包含的哈希值个数。

2.5 假阴性分析

算法的假阴性发生在局部敏感哈希函数产生假阴性并且在查询布鲁姆过滤器位数组时b 个位置不都为1。因此根据假阳性率的分析可得，算法的假阴性率为：

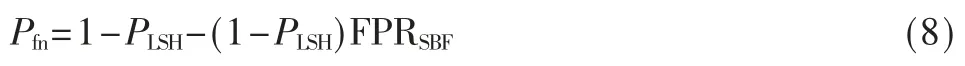
3 实验评估

3.1 数据集介绍

本文实验所使用的数据均来自真实数据集。

(1)CoverType 数据集

CoverType 数据集[17]属于一个分类数据集，该数据集有581 012 条不含缺失的数据，每条数据包含54 个维度，数据集线性不可分。具体来说，这54 个属性包括10个定量变量、4 个二元荒野地区和40 个二元土壤类型变量。

(2)HandWrite 数据集

手写字体识别数据集[17]是一个分类数据集，共有5 620个不重复且无缺失数据，每条数据都有64+1 个维度，其中前64 个维度都是0～16 之间的整数，最后一个维度是数据的标签。

3.2 评价指标

假阳性误判率(False Positive Rate，FPR)，如果一个查询数据不近似于插入到布鲁姆过滤器中的数据集合，但是查询返回true，这就是一个假阳性错误。

假阴性误判率(False Negative Rate，FNR)，如果一个查询数据近似于插入到布鲁姆过滤器中的数据集合，但是查询返回false，这就是一个假阴性错误。

3.3 实验结果及分析

为了检验近似查询布鲁姆过滤器的参数与查询速率以及误判率之间的关系，本节进行了参数实验，并固定布鲁姆过滤器位数组大小为m=224bit，使用的标准随机哈希函数的个数为b=3。插入到布鲁姆过滤器中的数据量为7 413 条，查询数据为3 177 条，总缺失率为0.005。

图3 是在数据集CoverType 下，固定条件(数据降到10 维、w=12、k 变 化时L=3、L 变 化时k=7) 下，L 与k 的值不断增加时，平均每条数据近似查询所需的时间曲线图。由图可知，当二者取值不断增加时，平均查询时间也随之增加，其中查询时间随k 呈指数增加，随L 呈线性增加。这是由于k 增加意味着每个gi组包含的哈希值增多，哈希计算所需时间增多，并且一个gi组除了自身外，还需检查2k 个扩展组，因此平均查询时间随k 呈指数增加，随L 呈线性增加。

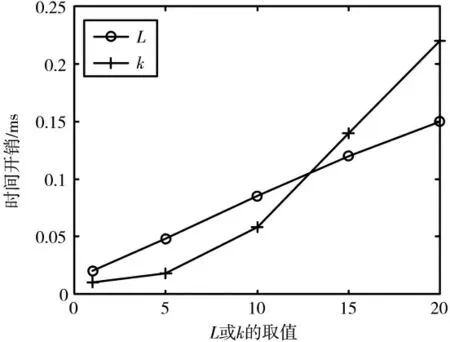
图3 平均查询时间

图4 为在CoverType 和HandWrite 数据集下，假阳性误判率、假阴性误判率的随L 变化曲线图。由图可看出在两个数据集中，当L 增加时，假阳性率均随之增加。

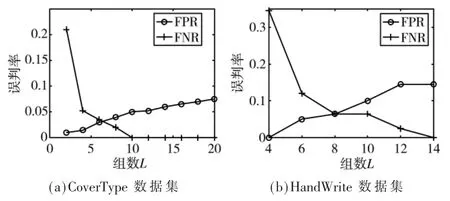
图4 两个数据集下不同L 取值的误判率

图5 为在CoverType 和HandWrite 数据集下，假阳性误判率、假阴性误判率随每组哈希函数个数k 变化的曲线图。当k 增加时，每个组的哈希值越多，在进行映射时，要将组内哈希值作为一个整体插入到位数组中，因此哈希值越多，组与组之间差异越大，碰撞的概率越小，假阳性率随之降低，假阴性率随之上升。

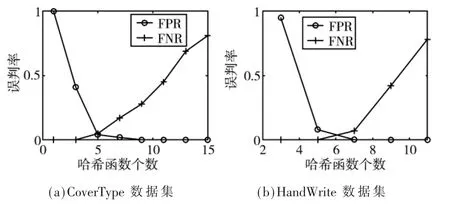
图5 两个数据集下不同k 取值的误判率

图6 为在两个数据集中，算法假阳性误判率以及假阴性误判率随p-stable LSH 哈希函数中桶宽w 的变化曲线图，从图中可看出，算法假阳性率随着w 的增加而增大，假阴性率随着w 的增加而减小。这是由于w 越大意味着桶宽越大，因此近似范围越大，落入同一桶的数据越多，哈希冲突的概率越大，假阳性率越大，同时相近的值越可能落入同一个桶，因此假阴性率越小。

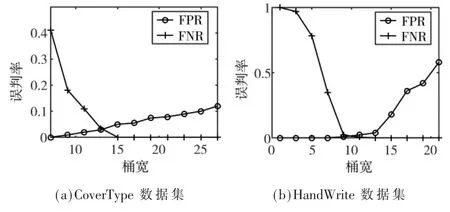
图6 不同w 下的误判率

图7 为在数据集CoverType 中，本节方案在不同的近似距离下误判率变化曲线图，实验时本方案将数据维度从54 维降到8 维，使用L=4 个组，每组使用k=6 个局部敏感哈希函数，同时设置桶宽w=12。图中显示随着近似性度量的欧氏距离增加，假阴性误判率渐渐增加，这是因为当距离增加，认为距离较远的点也近似于插入集合，但是原有的判定条件以及参数均不变，所以对于假阴性误判率，其分母真阳性数增加，但是原有的查询数目不变，而假阴性数目=真阳性数-查询出true 的数目，所以当真阳性数tp 增加时，假阴性误判率增加。同理，对于假阳性误判率，当真阴性数减小时，假阳性误判率减少。

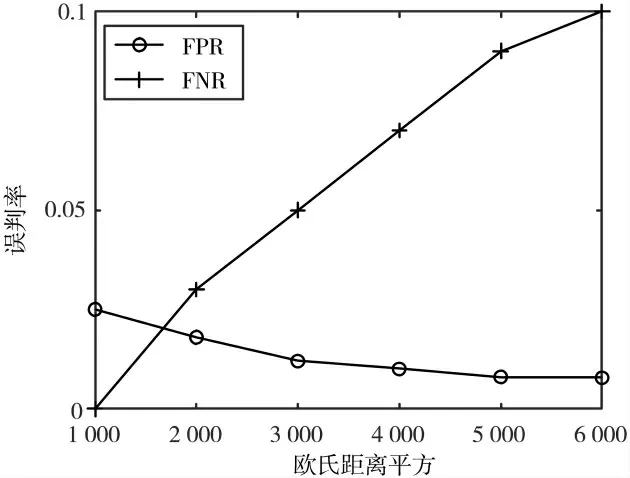
图7 不同欧式距离下的误判率

表1 中，在两个数据集下本方案将查询数据降维到不同维度然后进行近似查询，线性查找(Linear Search)在查询数据具有不同维度时进行暴力查询。由表可看出，本方案所需的平均查找时间比线性查询明显少得多。所谓线性查找就是遍历插入集合，计算查询数据与每一个插入数据的距离并判断是否小于指定值，若是则认为近似，因此线性查找所需时间与插入集合的数目有关。但是本文方案基于布鲁姆过滤器，所需查找时间仅仅与L、k、b 的值有关，通常这些参数较小且固定，算法是常数级查询时间，所以所需时间代价较小。从表中亦可看出，随着数据维度的降低，两者所需的平均查询时间均明显下降，基于降维的近似查找布鲁姆过滤器算法又通过降低查询数据维度进一步加快了查询速度。

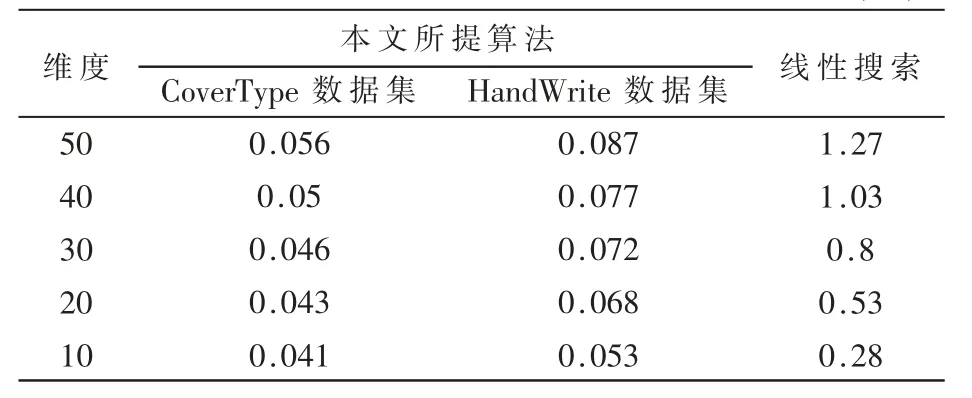
表1 不同维度下算法的平均查询时间(ms)

4 结论

本文提出了一种面向缺失数据的布鲁姆近似成员查询算法，可以判断查询的缺失数据是否与存储在布鲁姆中的数据相似。本文使用两个真实数据集对所提算法的有效性进行验证，在假阳性率、假阴性率和查询时间上，优于当前基于线性搜索的近似查询算法。