主动磁悬浮轴承鲁棒反步控制研究

2022-04-19叶志伟徐龙祥

机械制造与自动化 2022年2期

叶志伟，徐龙祥

(南京航空航天大学机电学院，江苏南京 210016)

0 引言

磁悬浮轴承也称电磁轴承，由于其具有能量损耗低、无机械接触、不需要润滑以及使用寿命长等优点[1]，广泛地应用于机械工业、能源交通、生命科学等领域[2]。而磁悬浮轴承系统中使用的控制器是影响其各种性能的一个比较重要的因素[3]。在实际工程中，PID控制在磁轴承控制中有举重若轻的地位。由于磁轴承自由度之间的陀螺力矩耦合、电磁铁之间的磁场耦合以及高速转子模态激发时出现的稳定性问题等，PID控制无法解决这些问题以满足需要的控制要求。因此，本文将为磁悬浮轴承系统设计基于反步法的鲁棒控制器，反步法不但能使系统具备跟踪性与稳定性，而且保留了系统中存在的非线性项，系统的精确性便能够得到保证[4]。反步法在设计时是通过递推的方式一步步地构造系统Lyapunov函数的，从而保证了系统的稳定性，并且其他方法如滑模控制、自适应控制等很容易与反步控制进行结合，因而可以设计出系统所需性能的控制器[5]。

1 系统设计磁悬浮轴承的数学模型

图1为五自由度的磁轴承转子受力分析模型图，转子是依靠磁悬浮轴承进行支撑的。系统工作时，转子的位置由传感器a和传感器b进行检测并且传输到使用的控制器中去。此时控制器对相应的偏差量根据不同的控制算法进行运算，然后将计算得到的控制电压信号输入到功率放大器中去，由功率放大器改变电流的大小传递给磁轴承线圈。因此磁轴承线圈的电流大小便会跟随控制器的变化而变化，使得磁轴承转子受到的合力不断变化，经过多次控制后，转子最终悬浮在中间。

图1 磁轴承转子受力分析模型图

磁悬浮轴承在实际工作时，其运转情况及结构都是很复杂的，这为建模带来不便，所以要做如下假设：磁轴承在径向方向上的结构和参数是一致的。转子为刚性回转体，并且转子绕x轴的转动惯量和绕y轴的转动惯量是相等的。当转子在运动时，可以忽略各个自由度之间的耦合作用，进行分散控制。依据以上假设可以得到转子的运动方程：

2 反步控制理论

反步法由Kokotovic等于1991年提出，它是通过为原系统的子系统设计李亚普诺夫函数，不断地满足子系统的要求进而得到原系统的控制律[6]。本文将设计一种鲁棒反步控制器，通过对实际系统的不确定性进行估计，使得系统可以获得更好的动态性能。

磁轴承系统的空间状态方程如下式所示。

假设系统的平衡点为xd，得到各个虚拟变量的定义：

其中ξ是设计的积分变量参数，可以减少外部的干扰所造成的误差。在设计时会对一个子系统构造相应的Lyapunov函数，从而保证每个子系统都能保持渐近稳定的特性。

定义Lyapunov函数

可得V1的导数为

将z2的导数代入：

当忽略不确定项d，那么可得V2的导数为

那么可以得到系统的控制量

由Lyapunov稳定性定律可知原系统的跟踪误差是可以收敛到0的。

为了估计不确定项d，增加控制器的跟踪性能和控制的鲁棒性，可以将非线性阻尼引入到控制器，控制律重新定义为

那么V2的导数变为

加入非线性阻尼后，具有未知的不确定上界控制律仍能保证系统一致渐近稳定，而且确保系统状态变量全局一致有界。通过调整各个确定干扰项对系统影响最小，达到系统全局渐稳定的目的：

3 仿真分析

根据上文设计的控制器在Simulink仿真环境进行了基于反步法的主动磁轴承控制系统仿真平台的搭建，如图2所示。为了验证设计的反步控制器是否拥有良好的性能，搭建了基于PID控制的主动磁轴承控制系统仿真平台与之进行对比分析，仿真平台如图3所示。假设磁轴承最终的平衡位置处于2.5V，初始位置为0V。系统进行仿真的参数是通过试凑法获得的较优的一组参数。仿真结果如图4所示。

图2 反步控制系统仿真平台

图3 PID控制系统仿真平台

图4 反步与PID控制下的系统阶跃响应图

从图4所示可知，设计的反步控制系统仅需0.01s便可以达到稳定状态，而PID控制系统则需要0.02s才能达到稳定状态，所设计的反步控制系统的响应速度是明显优于PID控制系统的，并且，设计反步控制下的系统没有表现出明显的超调量，而PID控制系统有0.2V的超调量。所设计的反步控制系统的超调量亦是明显优于PID控制系统的。

在实际的工作过程中，还有很多扰动因素会造成磁轴承系统无法保持稳定状态，因此本文主要进行了以下几个方面的扰动仿真：

1)阶跃扰动仿真

磁悬浮轴承转子实际工作时，可能出现突加负载扰动的情况，因此当转子悬浮在平衡位置后进行干扰的施加，在0.25s时对系统施加阶跃扰动信号，幅值为1A，如图5所示。采用反步控制的磁轴承系统的转子位移最大偏移值约为0.11V，PID控制下磁轴承系统的最大偏移值约为0.34V，反步控制相比PID控制转子位移偏移值减小了67.6%，而且PID控制的转子需要0.25s左右才能回到平衡位置；反步控制却仅需0.03s便能回到平衡位置，相比PID减少了88%的恢复时间。因此，采用反步控制的磁轴承系统抵抗阶跃扰动的性能是优于PID控制系统的。

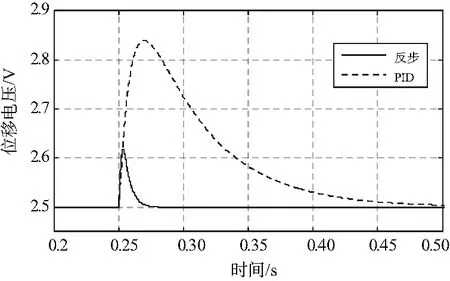
图5 施加阶跃干扰仿真对比图

2)周期性正弦扰动仿真

磁悬浮轴承转子实际工作时，可能出现突加正弦扰动的情况。因此当转子悬浮在平衡位置后进行干扰的施加，对系统施加频率为100Hz，幅值为1A的正弦扰动信号，如图6所示。采用反步控制的磁轴承系统转子最大偏移值约为0.15V， PID控制下磁轴承系统的最大偏移值约为0.32V，反步控制相比PID控制转子位移偏移值减小了53.1%。因此，采用反步控制的磁轴承系统抵抗正弦扰动的性能亦是优于PID控制系统的。

图6 施加正弦干扰仿真对比图

4 实验分析

为了验证设计的鲁棒反步控制器是否拥有良好性能，进行了转子四自由度的起浮实验。本试验使用的显示设备是Labview组件，Labview检测到的位移电压信号为0V～+5V。因此，当转子正常悬浮时，Labview显示的位移电压信号应该是2.5V。对于Labview显示的初始位移电压信号并不在0V，是因为使用了试验台转子结构的原因。使用本文设计的鲁棒反步控制器，对磁轴承系统试验台进行起浮试验，试验得到的磁轴承转子四个自由度的起浮效果如图7-图10所示。