国际多式联运收益分配博弈模型及Raiffa解优化

李 倩，刘 擎，吴群琪，闫柏睿

（1.长安大学 经济与管理学院，陕西 西安 710064；2.长安大学 综合运输经济管理研究中心，陕西 西安 710064)

0 引言

基于运输供应链整合的视角，由国际货代、铁路承运人、航运人等市场主体通过市场、运力、运营等各种资源整合构建国际多式联运物流联盟[1]，不仅有利于降低交易费用、产生协同效用，也是实现交通运输业高质量发展的重要路径[2]。相比发达国家，我国国际多式联运发展存在物流枢纽功能水平不足、联运设施设备标准不统一、信息互联互通水平不高、多式联运经营人资源整合能力弱等短板，以及收益分配不合理等管理问题[3]。其中，收益分配的公平合理性是影响物流联盟成员积极性、联盟稳定性的重要因素[4]，也是决定联盟能否为客户创造价值的重要因素。

基于多式联运物流联盟关系类型、成员行为、市场竞争水平等不同视角，国内外学者采用博弈论方法对联盟收益分配问题进行了一些探索。贺竹磬等[4]构建了主导企业与不同类型盟友的博弈模型，证明战略联盟关系下运输联盟收益分配应充分考虑盟友承担的风险及贡献水平；周永圣等[5]基于子博弈完美均衡的视角，将协同运输企业的地位与贴现因子相联系，证明贴现因子对合作收益均衡解具有重要影响；贺政纲等[6]关注到联运过程中企业决策和退出行为的动态性特征，引入惩罚因子建立扩展的蚁群劳动分工动态模型，为解决收益分配过程的动态性和公平性问题提供了借鉴。此外，考虑到市场单一联盟和多个竞争性联盟的不同情况，Song等[7]构建了上游海运公司整合下游铁路运输公司提供多式联运服务的博弈模型，发现双方收益受整合成本和效率的共同制约，率先制定批发价格的下游较上游会获得更高利润。综上可见，现有多式联运利益分配的相关研究大多聚焦于2个参与者的博弈过程，缺乏对多方参与的国际多式联运联盟收益分配问题的探讨。

Raiffa解是一种考虑收益分配上下限的合作博弈收益分配方法，更符合弱势参与方对收益分配结果的心理期望，且对信息收集的广度和数量要求低[8]，已被应用于物流联盟利益分配的诸多领域。相较于其他的物流联盟问题，国际多式联运物流联盟参与主体的运输工具及设施等资源持有量不尽相同，在枢纽型物流园、换装设施、信息平台系统等方面的专属建设成本投入额差异巨大，也受各方风险承担水平不同、实力强弱差异悬殊(联盟地位)、成本共担和收益共享综合契约等其他因素的影响[3]。为此，构建远洋运输公司、内陆铁路运输公司及中欧班列运营公司多式联运的联盟博弈模型，首先应用Raiffa解求解成本共担和收益共享综合契约条件下联盟各方的初始收益，在实证调查的基础上探索影响国际多式联运物流联盟的特质因素，识别并确定专属成本投入、运输资源持有量、合作风险、配合度、联盟地位5个特质因素，提出基于变异系数法和层次分析法确定特质因素权重及Raiffa解优化的思路，对初始收益分配结果进行改进，并以案例验证模型的有效性。

1 模型背景

1.1 问题描述

基于国际陆港的海—铁—铁国际多式联运是一种典型的联运模式，以东起日本神户西至德国汉堡的典型海—铁—铁联运为例，假设由3家运输企业分段承运日本的电子产品至德国，其中海运段承运人A远洋运输公司将承载着电子产品的集装箱从日本神户港海运至中国青岛，而后经内陆铁路段承运人B内陆铁路运输公司将其运抵中国西安，最后搭载C公司经营的中欧班列抵达德国汉堡。综合考虑运输里程和基础设施规模等因素，由B承担多式联运经营人，整合A和C建立联盟，各方共同投入建设联运设施以提高运输效率，吸引客户流量。假设作为理性参与者，各方根据预期收益确定是否组建联盟。

1.2 参数定义

多式联运联盟博弈模型参数定义如下。

Pi(i=A，B，C)——各阶段单位独立运输服务价格。

Ci——单位运输成本费用。

Di0——运输公司i所在市场的潜在市场容量。

αi——i的运输价格对需求的影响率。

Di——独立经营时各方的平均运输需求。

πi——独立经营时各方的收益。

ΔDik(i≠k)——与k合作后，i和k的运输需求增加量。

ΔCik——i，k合作后共同分担的总合作成本。

πik——i，k合作后总收益。

2 模型构建

构建A，B，C三方独立经营、两两结盟、三方联盟策略下的收益函数，利用Raiffa解对三方联盟总收益做出基于边际贡献的初始分配。

2.1 三方独立经营

A，B，C三方分别位于海洋运输、内陆铁路运输、跨国班列运输3个不同的服务市场，独立提供运输服务，有不同的初始运输需求。假设在运输服务市场中，A经营的海运成本低、运费低、运量大，B的专用线路开通和运营成本高导致单位服务收费高，C主营中欧班列运输业务、呈现良好的发展趋势，各企业竞争强度大，市场需求随价格波动。三方的收益表达式如下。

2.2 两两结盟

（1）若C独立经营，A和B结盟，实现神户—青岛—西安的国际多式联运。A和B共同投资升级码头技术设备、互联互通信息建设、仓储分拨中心建设等。假设运输效率提高吸引了新的客户需求，A，B各自运输量增加，额外收益大于分担的成本，其他因素不变，结盟后双方运输需求增加量为ΔDAB，建设联运基础设施总成本为ΔCAB，A和B分担的总成本比例为θAB，1 -θAB，总收益为

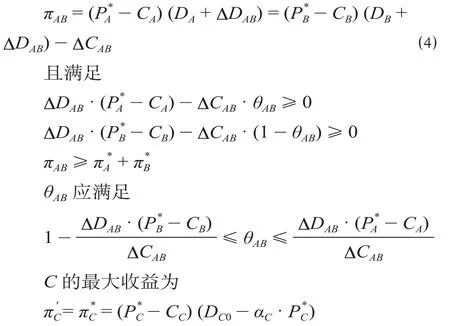
（2）若A独立经营，B和C结盟，实现青岛—西安—汉堡的国际多式联运。假设B和C共建集装箱铁路转运的作业平台、统一装载单元以优化集装箱转接流程等，运输效率提高吸引了新的客户需求，B，C运输总量增加，额外收益大于分担的成本，其他因素不变，结盟后双方运输需求增加量为ΔDBC，建设联运基础设施总成本为ΔCBC，B和C分担的总成本比例为θBC，1 -θBC，总收益为

（3）在研究背景中，受地理位置限制，A和C经营的线路之间无法通过构建基础设施实现运输的直接衔接以提高运输效率，假设结盟后总收益等于原独立经营时各方收益之和。

2.3 三方联盟及基于Raiffa解的初始收益分配

构建成本共担和收益共享综合契约下的收益分配模型。B作为多式联运经营人，整合A，C组建联盟，共同完成神户—青岛—西安—汉堡的国际多式联运。假设三方联盟使得各自运输需求增加量为ΔDABC，投入的干线整合成本、基础设施成本等和为ΔCABC，A，B，C各自分担的总成本比例为总收益为

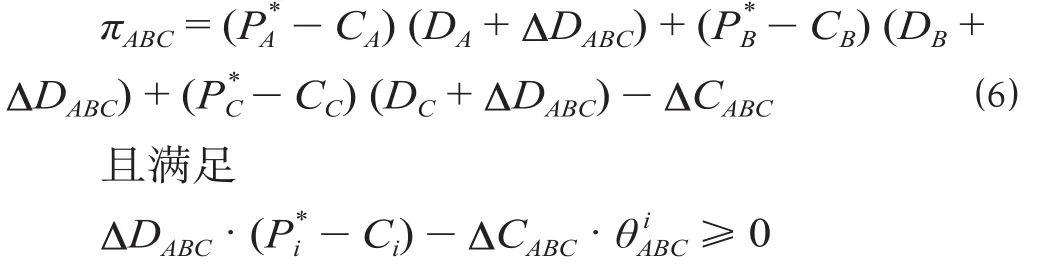
对于三方构成的集合I= {A，B，C}，其任一非空子集S⊂I对应的总收益为π(S)，满足

用xi表示参与方i对联盟收益πABC的期望收益，满足

根据Raiffa解计算此博弈的收益分配。

（1）记π(I/i) =bi表示无i参与时其余两方结盟的收益。从3个两两结盟获得的收益中得出各方分配的下限，记为

（2）相较于原来无k的两两结盟，k加入后形成三方联盟，总收益增加，增加的部分为k的边际贡献，记为先由k方和无k的两方平分，然后无k的两方内部等分，即

令k取A，B，C，重复上述步骤，然后求和、求平均，得到

将公式 ⑷ 至公式 ⑹ 代入公式 ⑺，可以得出在国际多式联运物流联盟中各方分配的收益xA，xB，xC。

从公式 ⑺ 中可以看出，当总收益πABC和联盟成员个数确定时，bi决定各方在联盟中收益水平的高低。由于bi表示没有i参与时其余两方获得的收益，bi值越小，该方对联盟的边际贡献越大。可见，Raiffa解仅将联盟内各方的边际贡献作为收益分配的参考指标，未考虑除边际贡献外的其他特质因素。

3 收益分配的特质因素及解优化

为确定国际多式联运收益分配的影响因素，对西安市国家多式联运示范工程项目、西安陆港多式联运公司、中外运物流有限公司、山东路桥国际货运代理有限公司等企业多式联运业务及联盟问题开展调研，最终确定了5个特质因素。专属投入成本和运输资源持有量作为定量因素通过实证调查获取；合作风险、配合度、联盟地位等属于定性因素，其值利用层次分析法(AHP)获得。通过把研究对象作为一个系统，按照分解、比较判断、综合的思维方式进行决策，AHP能够实现系统性的分析。同时，其还具有定性与定量相结合的优点，常用于具有分层交错评价指标的目标系统，处理目标值不易定量描述的问题[9]。通过邀请案例公司的10位业务经理和物流专家根据各公司的业务范围和整体表现进行两两比较，将上述定性因素按照“同等重要、稍微重要、较强重要、强烈重要、极端重要”及相邻判断的中间值量化为1-9的标度，构造判断矩阵，并进行单层排序与一致性检验，可以得到各方在上述定性因素方面的相对数值。为减少差异化的影响程度，取10种结果的平均值，可以得出各相对数值。

由于运输资源与合作风险分为多种，因此不同种类运输资源的权重、不同风险的权重在AHP得分的基础上利用变异系数法求解，其原理是变异程度越大的特质因素对收益分配结果的差异化影响越大，在修正初始收益分配额时应赋予较高的权重；相反，变异系数较小的特质因素，表明该项并非收益分配差额的主要影响因素，在修正模型中赋予的权重应较低。

3.1 专属成本投入

各方需共同参与中转专用运输线、枢纽型物流园、换装设施、信息平台等系统建设，以保证正常运转和高效衔接。联盟各方成本分担率不同，总投入占比大的一方通常获得较多收益补偿。此项数值根据联盟后各方为多式联运服务投资的现金总额来衡量，参考财务报表的账面价值，包括并不限于新购入的固定资产、流动资产及无形资产，记加和后的总投入成本为ΔCABC，分担成本比例由各方的成本投入除以总投入成本ΔCABC获得，求解修正后的比例与初始比例差为得到修正收益分配差额

3.2 运输资源持有量

根据Miller等[10]的研究，企业长期经营运输服务积累的资源包括知识资源(营销资源与管理资源)和物质资源(财务资源与组织冗余)2类，分别以未参与联盟前3年的以下指标的平均额来衡量：销售费用除以营业总收入、管理费用除以营业总收入，现金流除以总资产以及未分配利润额。研究首先根据实证调查获得的财务数据，确定以上指标的数值，然后计算各指标相较于B公司的比值，构造比例矩阵，其次利用变异系数法(各组比值的组内数据标准差与平均值之比)确定各类指标的权重，最后与比例矩阵相乘并进行归一化处理得到各方的综合运输资源持有量测度值γi，与初始测度值差为γi- 1/3，得到修正收益分配差额πABC×(γi- 1/3)。

3.3 合作风险

国际多式联运物流联盟面临运输服务整合风险、开辟新线路带来的收益不稳定、内部信息不对称等风险。选取运输服务整合风险、收益不稳定风险、内部信息不对称风险3类作为风险的测量维度，首先基于AHP的风险打分表确定各方面临的不同种类的风险水平，构造打分矩阵，取10种打分结果的平均值；其次利用变异系数法确定各类风险的权重，求解各方风险分担系数μi，得到修正收益分配差额

3.4 配合度

国际多式联运物流联盟配合度体现在各方在签订合同进行基础设施建设后的完成情况、是否与联盟参与方的竞争对手合作、集装箱换箱拼箱是否及时、是否维护联运服务整体形象等方面。当参与方对联盟业务表现出较高配合度时，内部实现有效协调，制定的运输业务计划高效完成，对于联盟的稳定性和效益产生正向影响。此项指标结合AHP的配合度综合水平打分表，经过数据归一化处理得到各方在联盟过程中的配合度因子τi，得到修正收益分配差额：

3.5 联盟地位

各方在国际多式联运物流联盟中的地位反映了其重要性程度和决策权力。多式联运经营人往往起着主导作用，具有较高的话语权，影响联盟的业务发展方向和水平。根据AHP结果，得到联盟地位评价指标δi，与初始指标的差为δi- 1/3，得到修正收益分配差额

最后，结合业务经理和物流专家对以上因素的重要程度两两比较打分，根据结果构造判断矩阵，利用AHP可求得各指标的权重分别为：ωC，ωS，ωR，ωA，ωI。

计算得到各方收益修正值为

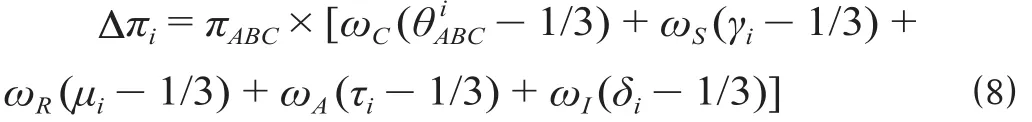
修正后的各方收益为

4 案例分析

研究以国际多式联运特定条件下的案例验证Raiffa解优化方法的适用性。其中，神户—青岛海运价格来源于对山东路桥国际货运代理有限公司的调研数据简化取整处理后的结果；铁路部分运输单价按照运输里程计算，其中青岛港—西安港的铁路运输里程约1 500 km，西安港—德国诺伊斯铁路运输里程约9 400 km，运费的构成按照20 ft箱的箱型、每箱20 t的电子产品、500元/TEU的发到基价和2元/(TEU·km)的运行基价计算，考虑附加与均摊等费用，为便于运算，将A，B，C公司的复合单位运价分别计为800元/TEU、4 000元/TEU、20 000元/TEU。考虑到疫情对运输业务带来的影响，选取2019年3个公司相应的业务指标确定成本费用Ci、需求量利润额需求增加量ΔDik、费用增加额ΔCik，Di0根据取整后2019年公布的全国集装箱吞吐量、全国内陆铁路集装箱运输量以及全国中欧班列集装箱运输总量确定，αi由上述数据根据公式 ⑵ 推算得到。

设A，B，C公司分别承担神户—青岛—西安—德国运输线路上海运、内陆铁路运输和中欧班列运输服务，由B担任多式联运经营人，整合A，C组建联盟，3家公司组成的所有非空子集S为：①三方独立经营——{A}，{B}，{C}；② 两两结盟 ——{(AB)，C}，{(AC)，B}，{(BC)，A} ；③三方联盟——{ABC}。

4.1 初始收益分配

结合1.2中各参数的取值范围，根据公式 ⑴ 至公式 ⑹ 得到独立经营时的参数值如表1所示，参与联盟后的参数值如表2所示。根据公式 ⑺，求得基于Raiffa解的三方联盟初始收益分配结果πi分别为：55 995 833.33，59 603 333.33，57 420 833.33，经比较均高于各自独立经营时的收益

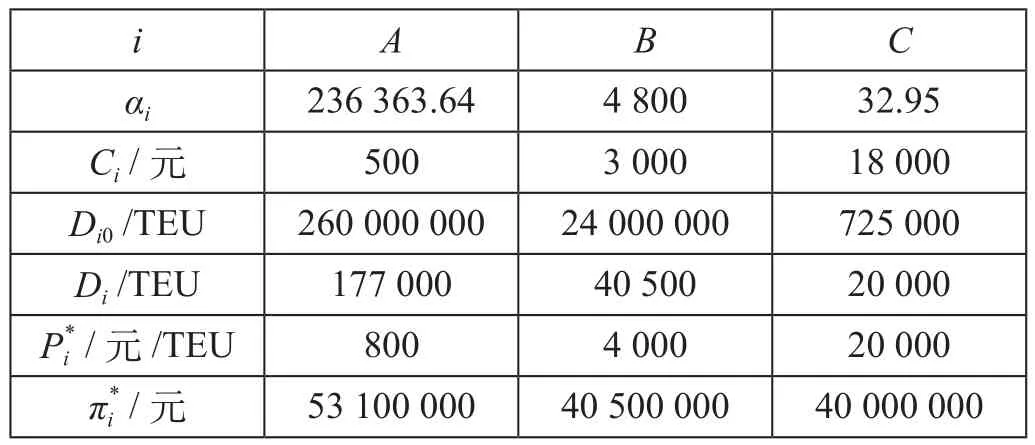
表1 独立经营时的参数值Tab.1 Parameter values under independent operation

表2 参与联盟后的参数值Tab.2 Parameter values under alliance participation

4.2 基于特质因素的Raiffa解优化

基于特质因素的Raiffa解优化步骤如下。

（1）将根据实证调查结果获得的5个主要特质因素的测度值结果填入表中。特质因素测度值如表3所示。

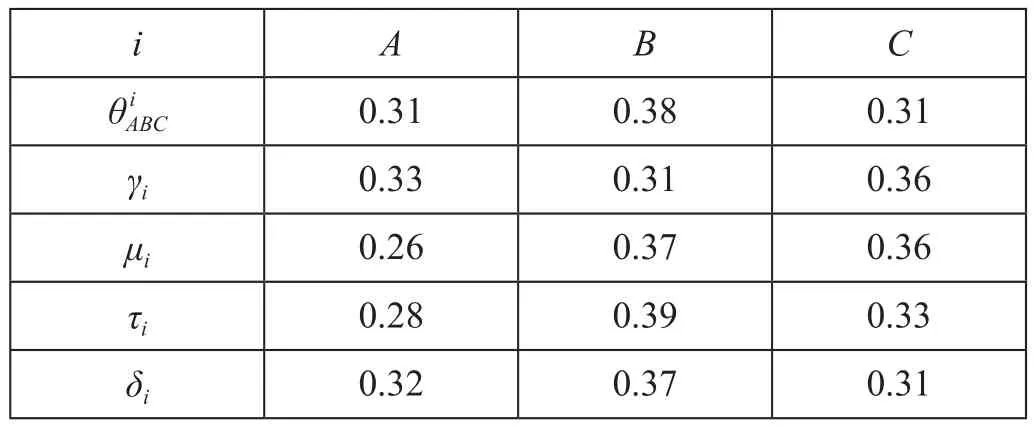
表3 特质因素测度值Tab.3 Measured values of idiosyncratic factors

整理特质因素重要性程度打分表，将得到的平均值近似、取整后的结果构造判断矩阵M。

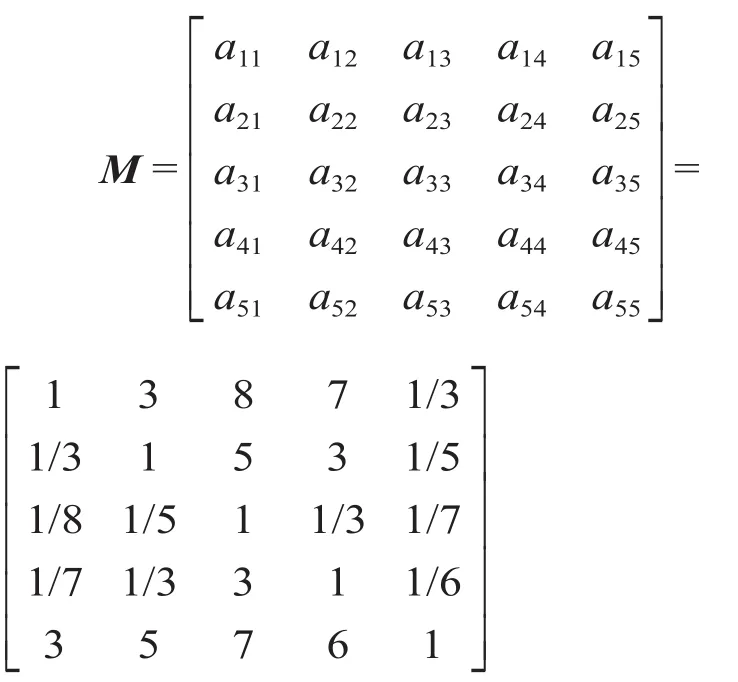
（2）对判断矩阵进行一致性检验：λmax= 5.35为上述矩阵的最大特征值，一致性指标0.09，查得n= 5对应的平均随机一致性指标RI=1.12，算得一致性比例一致性可以接受。

（3）对矩阵M进行归一化处理：得到M'=将归一化的矩阵各列相加，利用算数平均法求出各指标的权重分别为：ωC= 0.29，ωS= 0.13，ωR= 0.04，ωA= 0.07，ωI= 0.48，。

⑷ 根据公式 ⑻ 和公式 ⑼，得出利润调整差额Δπi和改进后的各方收益改进前、后三方收益变化如表4所示。三方联盟中，无论是否对收益结果进行Raiffa解优化，三方的收益πi均大于独立经营时的基于特质因素的Raiffa解优化后，A和C收益分配额均减少，而减少的收益之和由多式联运经营人B获得，原因在于其专属成本投入、合作风险、配合度、联盟地位4个指标都高于其他两方，相应的收益补偿具有合理性。

表4 改进前、后三方收益变化 元Tab.4 Comparison of three parties’ revenue changes before and after improvement

5 结束语

分析构建基于国际陆港的海—铁—铁国际多式联运物流联盟收益分配模型和参数确定方法，提出Raiffa解优化方法的思路，以特定条件下的案例验证得到以下结论：联盟收益大于独立经营的收益，定量揭示国际多式联运物流联盟可实现成员收益的帕累托改进；收益分配方案的制定需考虑5个影响国际多式联运物流联盟收益分配的特质因素，其中联盟地位和运输资源持有量是影响收益分配的关键因素，改进了传统Raiffa解仅考虑边际贡献的缺陷；Raiffa解优化方法对付出更多努力的多式联运经营人给予一定的收益补偿，具有合理性。研究可以为其他跨运输方式和跨区域的多式联运物流联盟收益分配提供理论与决策参考。