应用于光伏阵列故障诊断的DA-SOM算法研究

张晓阳，李田泽，张涵瑞，韩鸿雁，李 兵

（1.山东理工大学电气与电子工程学院，淄博 255049；2.国网德州供电公司，德州 253000）

近年来，光伏发电产业发展迅速，随着光伏发电系统不断投入使用，系统的故障诊断成为亟待解决的问题。光伏阵列由于自身的特点，通常安装在环境恶劣、高海拔地区，容易在冰雹、雨雪等恶劣天气的影响下发生开路、短路等各种故障，严重影响整个光伏发电系统的发电效率。因此，有效地诊断出光伏阵列的故障可以提高整个光伏阵列的发电效率，避免火灾等安全事故的发生，具有非常重要的意义。

针对光伏阵列故障诊断问题，文献[1]利用热成像仪检测光伏阵列发生故障时热性能的变化检测故障，但该方法成本高且用时长；文献[2]通过对比阵列的实测曲线与伏安特性曲线实现故障诊断，但该方法无法实现在线检测，一定程度上减少了光伏阵列的发电量。目前，国内外学者开始利用神经网络实现对光伏阵列的故障诊断，文献[3]提出了基于BP 神经网络的光伏阵列故障诊断方法，该方法主要是基于L-M 算法对故障状态参数进行处理，以最大功率点电流Im、最大功率点电压Um、短路电流Isc、开路电压Uoc为网络输入，以故障类型作为输出，并能够针对BP 神经网络的局部最优问题进行优化；文献[4]利用模糊C 均值聚类及隶属度算法，通过计算待诊断样本与各故障模式间的隶属度大小，实现故障诊断；文献[5]采用快速过采样主成分分析算法，通过对比阵列参考工作点与实测工作点，实现故障检测与识别。

自组织映射SOM（self-organizing map）神经网络因为收敛速度快、分类精度高等特点，在模式识别以及故障诊断等领域应用广泛[6]，文献[7]将SOM 神经网络应用于变压器的故障识别并获得较为准确的诊断结果；文献[8]在SOM 神经网络对输入样本进行初步聚类的基础上，再利用K-means 算法进一步聚类；文献[9]利用帝国竞争算法优化SOM 神经网络的参数进行故障诊断，提高了故障诊断准确率。

本文将SOM 神经网络应用于光伏阵列的故障诊断。在应用过程中，由于SOM 网络的分类精确度很大程度上取决于初始权值的选取，为获取最优权值，用蜻蜓算法DA（dragonfly algorithm）对神经网络的初始权值进行寻优。首先，构建DA-SOM 光伏阵列故障诊断模型，利用Matlab 仿真模拟各种故障，获取样本数据，选取光伏组件的开路电压、短路电流、最大功率点处的电压和最大功率点处的电流为输入特征向量，对模型进行训练并验证；最后将DA-SOM 算法的识别准确率与反向传播BP（back propagation）和DA-BP 进行对比，验证所提方法的先进性。

1 算法原理

1.1 SOM 神经网络

SOM 神经网络是一个无监督、无导师的自学习网络，与其他聚类算法相比，其不仅能够通过输入样本识别规律并识别出输入样本之间的关系，还能够学习神经网络的拓扑结构[10]。SOM 神经网络为两层结构，由输入层和输出层（竞争层）组成，输入层共有m 个神经元，输出层为n×k 个神经元，输入层与输出层实现全连接，其每个输出神经元都和输入神经元相连接[10]，连接的强度由连接权值表示。

SOM 神经网络的基本思想为：在对一个输入向量进行学习时，输出层各神经元竞争对输入向量的响应机会，产生一个获胜神经元，在进行权值更新时，获胜神经元周围的权值都会得到更新调整。经过学习和训练，竞争层中的每一个神经元都对某一类输入向量最为敏感，从而使输入层中有关联的数据在输出层也能够聚在，实现聚类。

SOM 算法对数据进行聚类主要分为如下3 步。

第1 步 对于每一个输入向量，计算输入数据与输出层每一个神经元之间的欧式距离，找出距离最小的获胜神经元，其数学表达式为

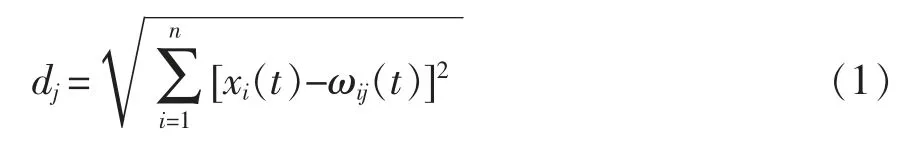
式中：dj为输入数据xi（t）与输出层神经元之间的欧式距离；ωij（t）为输入层第i 个神经元和输出层第j个神经元之间的权值。

第2 步 确定获胜神经元的一个邻域范围，一般由邻域函数确定。本文的邻域函数采用Gaussian函数，函数形式为

式中：hij为拓扑领域，该领域函数定义的是以获胜神经元为中心；δ 为获胜领域范围的半径，称为领域半径。

第3 步 对竞争获胜神经元及邻域内的权值向量进行调整，使其向输入向量X 靠拢，数学表达式为

式中：η（t）为学习速率，随着时间t 的增加而减小；ωi（t）为获胜神经元及领域内的权值向量，当2 个神经元同时被激励，则两者之间的权值连接会被增强，反之被削弱。

1.2 DA 算法原理

蜻蜓算法的原理就是模拟蜻蜓觅食过程，在觅食过程中，蜻蜓个体主要包括以下5 种行为[11-13]。

（1）规避。蜻蜓个体之间相互保持安全距离，该行为的位置更新公式为

式中：Xm为第m 个邻近个体的位置；X 为当前个体的位置；N 为相邻个体的数量。

（2）列队。蜻蜓个体使自己与周围群体内其他个体速度保持一致，该行为的位置向量更新公式为

式中，Vm为第m 个邻近个体的行进速度。

（3）聚集。蜻蜓个体向蜻蜓群体周围其他个体靠近，该行为的位置向量更新公式为

（4）寻找食物。蜻蜓个体寻找食物的更新公式为

式中，X+为食物源的位置。

（5）规避外敌。蜻蜓个体在寻找食物过程中躲避外敌攻击，该行为计算公式为

式中：Ei为蜻蜓躲避外敌时的位移位置；X-为蜻蜓天敌所在的位置。

蜻蜓群体行为是以上5 种行为模式的组合，通过步长ΔK 的调整来实现位置的更新，更新公式为

式中：s、a、c、f、e 分别为5 种行为对应的权重；w 为惯性权重。

当有邻近蜻蜓时，位置向量更新公式为

当周围无邻近蜻蜓时，蜻蜓个体的游走行为遵从

式中：k 为当前迭代次数；d 为向量维数；Le'vy（·）为计算而得的飞行函数。

1.3 DA-SOM 算法流程

运用DA 算法对SOM 神经网络权重失真指数LWDI（locally weighted distortion index）进行寻优。为了对神经网络性能做出综合评价，其适应度σfitness计算公式为

式中：X 为输入向量；E 为数学期望；ω（g1，g2）为坐标为（g1，g2）的神经元的权值；（c1，c2）为输入向量X的获胜神经元的坐标；hx（·）为邻域函数。

DA-SOM 算法优化步骤如下。

步骤1读取故障特征数据，对输入数据进行归一化处理，并分为训练数据和测试数据。

步骤2初始化蜻蜓算法和SOM 网络参数，确定蜻蜓算法种群数量G 和最大迭代次数kmax。

步骤3将训练数据输入神经网络，根据式（12）计算蜻蜓个体的适应度函数。

步骤4更新蜻蜓个体位置和速度。

步骤5计算适应度。如果当前蜻蜓的适应度优于已保存的最优适应度，则用该适应度替换之前保存的最优适应度，并保存当前最优值所对应的参数；反之，保留之前的最优参数。

步骤6若迭代次数k>kmax，则保留最优输入权值；反之k=k+1，转到步骤4。

步骤7输出寻优获得的最优参数，将最优初始权值代入SOM 模型。

2 基于DA-SOM 的光伏阵列故障诊断模型

2.1 光伏阵列故障特征量选取

本文搭建的光伏阵列模型是由24 个光伏电池模块通过串并联组成的8 行3 列光伏阵列，即包含3 个并联的光伏组串，每个光伏组串由8 个光伏电池模块串联而成。其中，光伏电池模块参数如下：短路电流Isc为7.84 A，开路电压Uoc为36.3 V，最大功率点处电流Imp为7.35 A，最大功率点处电压Ump为29 V。本文模拟的4 种常见故障类型包括光伏组件开路和短路、阴影遮挡导致的热斑故障以及组件性能退化从而引发的老化故障。

不同内阻及不同光照强度下输出的U-I 曲线如图1 和图2 所示。分析图1 和图2 可知，异常老化（通过改变光伏电池模型中的串联电阻实现）故障状态下，光伏阵列的开路电压和短路电流基本不变，但最大输出功率以及最大功率点处的电压和电流有所下降；热斑故障（通过改变组件区域光照强度实现）发生时，被遮挡组件输出降低，由供能元件变为耗能元件，光伏电池输出的开路电压和短路电流与正常状态相比都有所下降；当开路故障发生时，光伏阵列输出的短路电流和最大功率点处电流很小，开路电压和最大功率点处电压基本不变；当短路故障发生时，光伏阵列输出的开路电压和最大功率点处电压有明显下降，短路电流和最大功率点处电流基本不变[14]。因此，本文选取光伏阵列的开路电压、短路电流、最大功率点处的电压以及最大功率点处的电流为特征参数作为神经网络的输入对光伏阵列故障进行诊断。

图1 不同内阻下的U-I 曲线Fig.1 U-I curves with different values of internal resistance

图2 不同光照强度下的U-I 曲线Fig.2 U-I curves with different values of light intensity

2.2 光伏阵列故障定位

本文采用的传感器摆放位置如图3 所示，故障的定位过程可主要分为两步。

图3 光伏阵列传感器安装位置Fig.3 Placement of photovoltaic array sensor

首先，找到故障单元所在的支路。当开路故障发生时，故障组件所在整条支路电流为0；短路故障发生时，工作状态的组件数量减少，输出电流随之减小，致使光伏阵列输出电压降低；阴影和老化故障发生时，故障元件在支路中等同于负载，导致整条支路的输出电流减小。因此，通过测量每条支路上的电流即可确定故障支路。

其次，通过测量该故障支路每个组件的电压值，找到故障组件所在的位置。由于故障发生时，支路电流减小，导致该支路正常组件的输出电流同时减小，此时流过旁路内阻和二极管内的电流会增大，导致正常组件的输出电压高于正常值[15]，进而通过输出电压确定具体组件故障位置。

2.3 故障诊断模型的建立

基于蜻蜓算法优化SOM 神经网络的光伏阵列故障诊断模型如图4 所示。

图4 DA-SOM 神经网络故障诊断模型Fig.4 DA-SOM neural network fault diagnosis model

首先将提取的故障数据样本进行归一化处理，作为故障诊断模型的输入；然后将4 种故障类型作为神经网络的输出，并利用蜻蜓算法对神经网络的权重失真指数进行寻优来获取最优初始化权值组合；最后根据寻优获得的最优参数建立故障诊断模型。

3 实验仿真分析

将选取的150 组光伏阵列故障运行状态特征向量代入SOM 神经网络进行训练，选择输出层为6×6 的36 个神经元，设定训练步数分别为10、50、100、200。不同训练步数的聚类结果如表1 所示，表1 中聚类结果的数字代表着各自故障在输出层神经元上的位置。当训练步数到达100 时，4 种故障类型被完全分开；而随着训练步数的增加，训练时间也会增加，因此选择训练步数为100 时，不仅能保证诊断准确率，同时能够减少运行时间。

表1 不同训练步数聚类结果Tab.1 Clustering results with different training steps

设置蜻蜓算法参数为：种群规模G=40，最大迭代次数kmax=20。经过DA-SOM 神经网络训练后，输出层神经元激活结果如图5 所示，其中神经元6、1、36、31 分别代表T1（开路）、T2（短路）、T3（热斑）、T4（异常老化）4 种故障。

图5 DA-SOM 神经网络训练结果Fig.5 Training results of DA-SOM neural network

训练结束后，自故障样本数据中随机选取24组故障数据进行诊断，输出结果如图6 所示，图中C 代表故障数据样本，C1—C6、C7—C12、C13—C18、C19—C24分别代表开路、短路、热斑和异常老化故障数据样本，对于每一种故障输入，都有对应的输出层神经元被激活，相同故障类型的故障数据对应输出层神经元的位置重合或距离接近。由图6 可知，C13、C18两组故障数据被诊断为异常老化故障，为错误诊断；开路、短路故障诊断均为正确诊断。

图6 DA-SOM 神经网络故障诊断结果Fig.6 Fault diagnosis results of DA-SOM neural network

自组织映射神经网络初始权值的选取具有一定的随机性，这对算法的收敛性能有直接影响。对于一个稳定算法来说，经过多次实验，算法的LWDI收敛值变化应该很小，即该算法对初始权值选取的敏感度较低。因此利用蜻蜓算法对SOM 神经网络初始权值进行寻优。LWDI 随迭代次数变化情况如图7 所示。由图7 可以看出，SOM 算法LWDI 收敛值波动较大，即对初始权值选取的敏感性较高，进而影响网络的聚类质量。而本文提出的DA-SOM 算法LWDI 收敛值波动较小，因此DA-SOM 算法聚类效果较优。

图7 LWDI 随迭代次数变化情况Fig.7 Changes in LWDI with the number of iterations

为验证DA-SOM 神经网络的故障诊断结果，随机选取24 组光伏阵列故障数据进行实验，并将诊断结果与BP 和DA-BP 神经网络对比，其中BP 神经网络参数设置如下：训练误差为0.001，步长为0.1，训练次数为1 000。4 种诊断模型的诊断正确率如表2 所示。由表2 可以看出，通过多次仿真得到的诊断正确率均值可知，DA-SOM 神经网络的诊断正确率要高于其他3 种神经网络。

表2 4 种诊断模型的诊断正确率Tab.2 Diagnostic accuracy of four diagnostic models

4 结语

本文将SOM 神经网络应用于光伏阵列故障诊断研究，并针对原始SOM 神经网络对初始权值敏感的缺点，采用蜻蜓算法优化SOM 神经网络的局部权重失真指数，将寻优获得的最优解作为SOM神经网络的初始权值，与基本SOM 神经网络、BP以及DA-BP 神经网络相比，改进后的神经网络聚类质量得到明显提高，对光伏阵列故障数据能够得到较优的诊断结果，诊断正确率有大幅提高，因此对光伏阵列故障诊断研究具有一定的研究价值。