不平衡电压暂降下考虑电流峰值的多目标光伏逆变器控制策略

佘 然，徐永海，蒋海玮

（新能源电力系统国家重点实验室（华北电力大学），北京 102206）

近年来，随着清洁能源的大力发展，光伏逆变器在电网中所占的比例越来越高，因而光伏逆变器在电网中的运行问题得到了越来越多的重视[1]。电网发生电压暂降会造成一定程度上的电压不平衡，此时出现的负序分量会使光伏逆变器输出的有功功率与无功功率发生波动，造成输出电流不对称[2]。此外，发生电压暂降时，光伏逆变器的输出峰值电流突然增大，可能导致光伏逆变器内的开关器件烧毁，造成光伏逆变器低电压穿越失败[4]。

针对不平衡电压暂降下光伏逆变器峰值电流的控制策略，文献[3]提出了基于消除有功功率波动且抑制峰值电流的光伏逆变器控制策略，但在消除有功功率波动的同时造成输出无功功率波动较大；文献[4-5]提出了在已有参考电流算法基础上加入多个调节参数的控制策略，分析了功率波动、输出电流谐波以及峰值电流同各参数之间的关系，但调节参数过多，且功率波动减小效果不明显；文献[6]提出了一种计算输出有功/无功功率参考值的逆变器峰值电流控制策略，实现了零有功功率振荡，但存在无功振荡过大的问题；文献[7]提出了一种电网不对称情况下的逆变器峰值电流控制策略，该方法可以有效地将输出电流控制在峰值电流以内，但存在负序电流过大与输出电流不对称的问题；文献[8]提出了一种基于FPNSC 算法的峰值电流控制策略，通过灵活设定正、负序控制因子实现不同控制目标下的逆变器控制，但存在只能控制单一目标如消除有功功率波动而无法兼顾其他目标的问题；文献[9]提出了一种消除有功功率振荡的光伏逆变器低电压穿越控制策略，但会造成峰值电流过大；文献[10]提出了一种电网不对称时抑制负序电流的并网逆变器控制策略，该方法可以有效抑制负序电流，使逆变器输出对称的三相电流，但存在输出有功/无功功率波动问题；文献[11-13]仅讨论了不平衡电网下的逆变器控制策略，没有考虑峰值电流问题。

本文提出了一种考虑电流峰值的多目标光伏逆变器低电压穿越控制策略。首先基于多目标人工蜂群算法与标准满意度算法求解多目标参数，并利用已得到的峰值电流控制输出有功/无功，达到使峰值电流、有功功率波动、无功功率波动与负序电流相对较小的目标。

1 光伏逆变器数学模型

光伏逆变器的典型拓扑为三相桥式拓扑，其基本结构如图1 所示。图中，Udc为光伏阵列产生的直流电压，L 和R 为光伏逆变器的输出电感和电阻，三相交流电源与光伏阵列通过逆变器相连。在三相abc 坐标系下，由基尔霍夫电压定律可得光伏逆变器三相电压表达式为

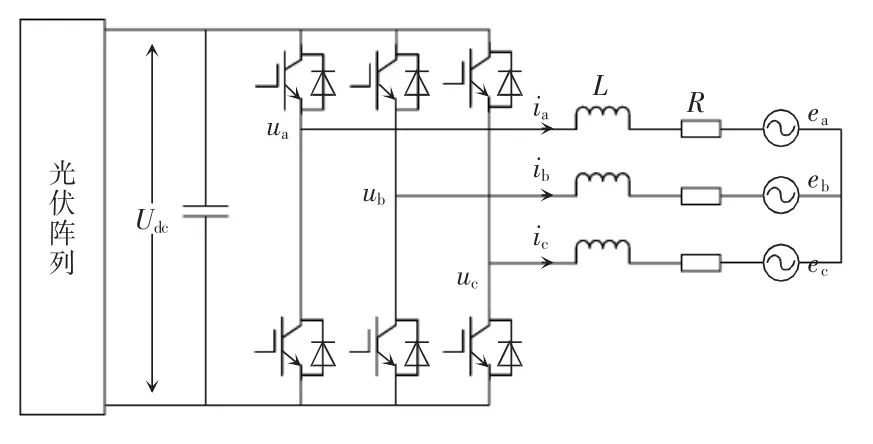
图1 三相桥式光伏逆变器主电路拓扑Fig.1 Main circuit topology of three-phase bridge PV inverter

式中：ua、ub、uc为逆变器侧电压；ia、ib、ic为逆变器流过的电流；ea、eb、ec为电网侧电压。

通过Park 变换，可将三相abc 坐标系下的交流量转换为同步旋转dq 坐标系下的直流量。同步旋转dq 坐标系下的电压表达式为

式中：ud、uq为逆变器侧电压ua、ub、uc在d、q 轴上的投影；id、iq为ia、ib、ic在d、q 轴上的投影；ed、eq为ea、eb、ec在d、q 轴上的投影。

电网发生电压暂降时电网出现三相不平衡会出现负序分量。忽略电阻R，此时光伏逆变器在正负序dq 轴下的电压表达式为

2 不平衡电压暂降下考虑电流峰值的多目标控制策略

2.1 多目标电流参考值推导

由瞬时功率理论[14]可得光伏逆变器输出的有功功率与无功功率，即

式中：P0、Q0分别为有功功率、无功功率的平均值；Pc2、Ps2分别为有功功率的2 倍频波动分量幅值；Qc2、Qs2分别为无功功率的2 倍频波动分量幅值。

当电网电压出现不平衡时，P0、Q0、Pc2、Ps2、Qc2、Qs2可表示为

设置参数k 做简化处理，令k 的范围为[-1，1]，则

可得到多目标电流参考值表达式为

式中：D1=1+kλ2；D2=1-kλ2；λ=U-/U+。其中，k=-1 时为目标3；k=0 时为目标1；k=1 时为目标2。

2.2 峰值电流表达式推导

电网发生不平衡故障时会产生负序电流，导致参考电流过高，使光伏逆变器输出电流过高，造成逆变器低电压穿越失败现象[4]，因此，对光伏逆变器的峰值电流进行控制有极大的必要性。将式（12）进行反Park 变换，可得到输出电流在三相abc 坐标系下的表达式为

式中：K1=P0/D1；K2=kλP0/D1；K3=Q0/D2；K4=kλQ0/D2；θ+=ωt+φ+；θ-=-ωt+φ-，且θ+、θ-使得。

将式（13）进行变形得到

式中：ψ=θ++θ-；φ1=arctan（K3/K1）；φ2=arctan（K4/K2）。

由式（14）可得到三相电流的峰值表达式为

令Q=hP，可将式（15）简化为

2.3 参数k 的确定

将式（12）参考电流代入式（6），可以得到有功功率波动与无功功率波动的表达式，即

则相对电流不平衡度的表达式为

根据式（17）～式（19）可以发现，Pc2、Ps2、Qc2、Qs2、Δγ2不可能同时为0，即不能同时消除有功功率波动、无功功率波动、电流不平衡度，但通过选择多目标算法确定k 值，可兼顾3 个控制目标。

2.3.1 多目标算法的选择

针对前面3 个目标无法同时兼顾的问题，本文提出了基于多目标人工蜂群MOABC（multi-objective artificial bee colony）算法的控制策略。人工蜂群算法由Karaboga 于2005 年提出[15]，具有结构简单、易于实现、参数少等优点，其基本思想来源于蜂群通过个体分工和信息交流相互协作完成采蜜任务。生物学家研究发现蜜蜂以跳舞的方式来交换蜜源信息。采集到花蜜的蜜蜂返回到蜂巢后，通过“8 字舞”的形式与同伴交流蜜源信息。引领蜂跳“8 字舞”的持续时间与蜜源的质量呈正相关，跟随蜂根据观察到的舞蹈选择蜜源进行采蜜。图2 为MOABC 算法的基本流程。

图2 MOABC 算法流程Fig.2 Flow chart of MOABC（multi-objective artificial bee colony）algorithm

MOABC 算法目标函数的表达式为

2.3.2 最终解的确定

上述算法只能得到MOABC 算法最优解集中的解，还需根据实际系统的运行情况筛选出决策者满意的最优解，本文采用最大满意度法求解最终的最优解。根据隶属度函数求解每个最优解对应的各目标函数的满意度，标准化满意度最大的解为最优解。各最优解的标准化满意度计算公式为

式中：μk为第k 个最优解的标准化满意度；N 为最优解的个数；M 为目标函数的个数。

常用的满意度解析式分为偏小型满意度解析式、中间型满意度解析式、最大型满意度解析式[15]。本文的求解目标是式（20）的值尽可能接近0，属于偏小型满意度解析，所以采用偏小型满意度解析式，即

式中：fm为第m 个目标函数；fmmin和fmmax为解集中第m 个目标函数的最小值与最大值。

不平衡度为0.2～0.5 时，不同最终解k 所对应的有功功率波动ΔP、有功功率波动ΔQ 与电流相对不平衡度Δγ 的求解结果如图3 所示。

图3 不同平衡度下有功/无功功率波动及电流相对不平衡度Fig.3 Relative imbalance degree of current and active/reactive power fluctuations under different balance degrees

2.4 输出电流峰值控制策略

在求得参数k 后，根据式（16）可进一步求得光伏逆变器在峰值电流运行时的功率表达式为

式中，Imax为光伏逆变器允许通过的最大电流，即峰值电流。

电网发生不平衡故障时，为限制光伏逆变器峰值电流，光伏逆变器按最大允许电流运行，输出的有功功率与无功功率即为式（23），此时为峰值电流运行模式，将按式（23）得到的有功功率参考值代入式（12）得到新的电流参考值，进而对逆变器进行控制。

3 仿真分析

在PSCAD/EMTDC 平台搭建光伏仿真模型，系统控制框图如图4 所示，Ud和Ud1为光伏系统最大功率点跟踪MPPT（max power point track）控制得到的直流侧电压及其参考值，Ud1与Ud的差值经调节后得到有功功率参考值Pset1和逆变器输出无功功率参考值Qset1，此时光伏逆变器按额定有功功率运行。当电网电压不对称时（电压出现明显的负序分量），为限制电流峰值，光伏逆变器按照式（23）求出的Pset2、Qset2输出有功功率、无功功率，此时光伏逆变器按最大电流峰值运行。通过此时的有功功率、无功功率参考值计算正负序dq 轴下的多目标电流参考值，经过PI 调节后得到正负序dq 轴下的电压参考值。仿真参数如表1 所示。

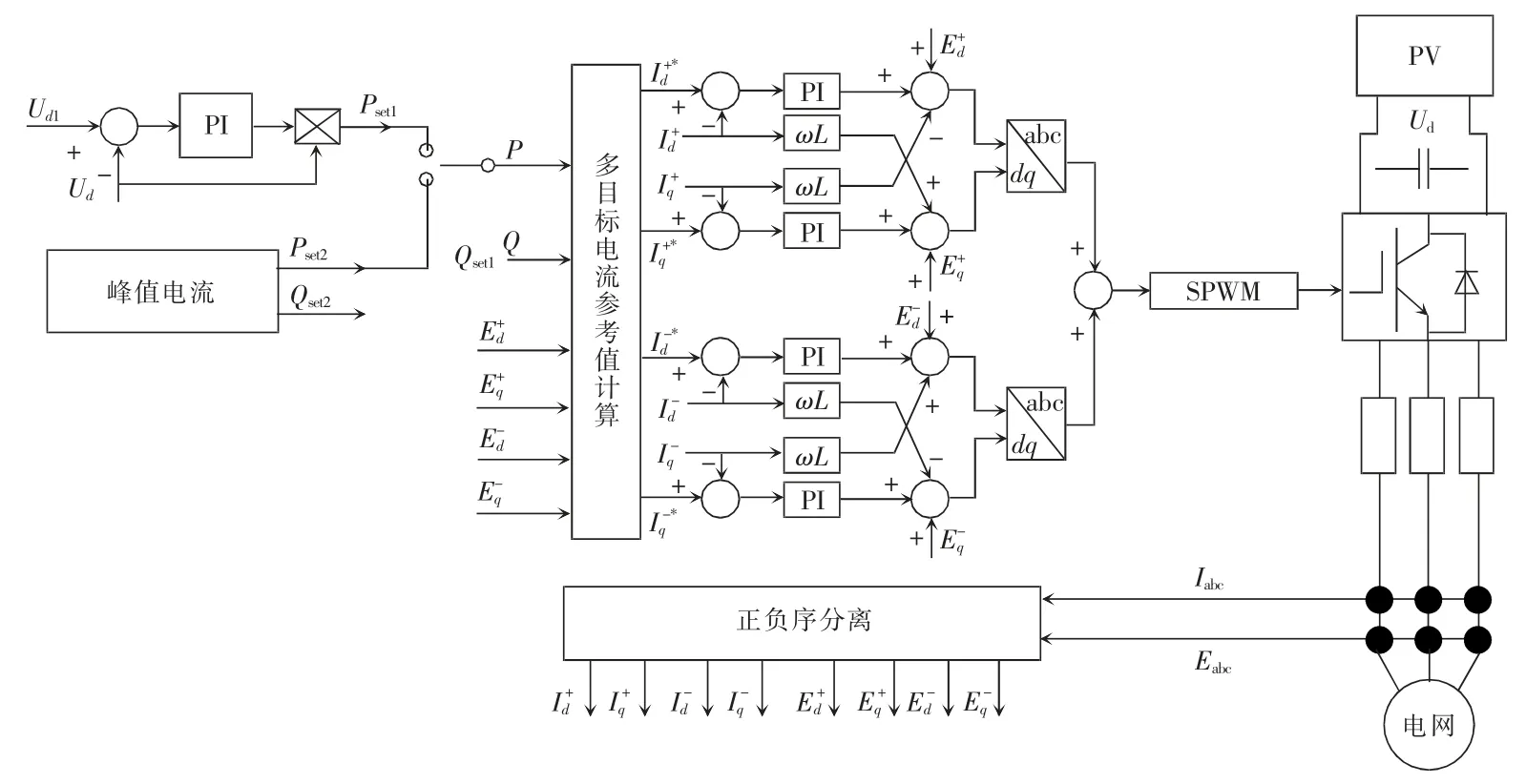
图4 系统控制框图Fig.4 Control block diagram of system

表1 光伏模型仿真参数Tab.1 Simulation parameters of PV model

稳定情况下光伏逆变器按额定功率运行，此时光伏系统采用MPPT 扰动观察法控制，输出的最大电流Imax为额定电流IN的1.5 倍，即Imax=1.5IN=1.5 kA；输出的有功功率P0即为额定有功功率P；输出的无功功率为Q0，设定此时的Q0=0。

算例1：在t=2 s 时发生电压暂降，出现三相电压不平衡现象，不平衡度为λ=0.4。令h=0.5，即Q=0.5P，将上述参数代入式（17）～式（19），并采用MOABC 算法与标准化满意度算法求解参数k。此时光伏逆变器按峰值电流模式运行，输出的有功功率与无功功率参考值按式（23）计算。

图5 所示为MOABC 算法得到的最优解与真实解，其中真实解为k 从[-1，1]每隔0.05 取值所得。可以看出，最优解集与真实解集在同一条曲线上，说明算法真实有效。经过MOAB 算法得到的最优解集按式（21）～式（22）计算得到此时的k=-0.34。

图5 MOABC 最优解与真实解Fig.5 Optimal solution obtained by MOABC algorithm and real solution

图6 为λ=0.4 时传统控制策略仿真波形。图6（a）为λ=0.4 时传统单一目标峰值电流控制策略，可以看出，在t=2 s 时电网出现不平衡现象，此时电流峰值很好地控制在Imax=1.5 kA 内，可有效保证光伏逆变器渡过电网不平衡阶段，输出的有功功率几乎无波动，而输出的无功功率波动较大，负序电流较大，无法输出对称的三相电流，为目标3 的控制方式。

图6 λ=0.4 时传统控制策略仿真波形Fig.6 Simulation waveforms of traditional control strategy when λ=0.4

图6（b）为λ=0.4 时额定功率下的多目标控制策略，设定此时的有功功率P=0.5 MW，无功功率Q=0 Mvar。同样在t=2 s 时电网出现不平衡现象，此时输出的有功功率与图6（a）相比出现较小波动，输出的无功功率与图6 相比波动减小较多，负序电流在t=2.05 s 后降低明显，但输出电流已超出Imax=1.5 kA，容易造成光伏逆变器低电压穿越失败。因此，将Imax=1.5 IN代入式（23），得到此时的Pset=0.41 MW，Qset=0.205 Mvar，将其代入式（12），得到如图6 所示的仿真波形。

图7 为λ=0.4 时峰值电流运行下的多目标控制策略仿真波形，在t=2 s 时电网出现不平衡现象，此时输出的有功功率与图6（a）的传统单一控制目标相比，波动从0 增加到0.12 MW，相对波动为24%。输出的无功功率与图6（a）相比，波动从0.34 Mvar 减少到0.21 Mvar，相对波动为42%。而相对电流不平衡度与图6（a）相比，从22%减小到1.8%，负序电流减小较明显。此外，与图6（b）额定功率下的多目标控制策略相比，有功/无功功率波动、电流相对不平衡度基本相同，但峰值电流有效的控制在Imax=1.5 kA 以内。

图7 λ=0.4 时考虑电流峰值的多目标控制策略仿真波形Fig.7 Simulation waveforms of multi-objective control strategy considering current peak value when λ=0.4

算例2：与算例1 类似，在t=2 s 时发生电压暂降，出现不平衡现象，此时不平衡度为λ=0.3，运用MOABC 算法与标准化满意度算法求解参数k=-0.21。

图8 为λ=0.3 时传统控制策略仿真波形，可以看出，在t=2 s 时电网出现不平衡现象，此时图8（a）的电流峰值很好地控制在Imax=1.5 kA 内，可有效保证光伏逆变器渡过电网不平衡阶段，但同样存在输出的无功功率波动较大、负序电流较大、无法输出对称的三相电流的问题。图8（b）表明无功功率波动与负序电流减小，但存在输出电流峰值Imax超过1.5IN的问题。此时将Imax=1.5IN代入式（23），得到此时的Pset=0.43 MW，Qset=0.21 Mvar，考虑电流峰值的多目标控制策略仿真波形如图9 所示。可以看出，与图8（a）单一控制目标峰值电流控制策略相比，有功功率波动从0 MW 增加到了0.08 MW，相对波动为16%；无功功率波动从0.24 Mvar 减少到0.14 Mvar，相对波动为28%；电流相对不平衡度从17%降低到0.39%。与图8（b）相比，电流峰值有效控制在1.5IN以内，而有功/无功功率波动、电流相对不平度相同。具体对比结果如表2 所示。

表2 对比分析Tab.2 Comparative analysis

图8 λ=0.3 时传统控制策略仿真波形Fig.8 Simulation waveforms of traditional control strategy when λ=0.3

图9 λ=0.3 时考虑电流峰值的多目标控制策略仿真波形Fig.9 Simulation waveforms of multi-objective control strategy considering current peak value when λ=0.3

4 结语

本文提出了一种考虑峰值电流的多目标光伏逆变器低电压穿越控制策略，该方法使有功功率波动、无功功率波动和负序电流较小，并使光伏逆变器的电流限值在峰值电流以内。仿真结果表明，光伏逆变器在本文所提控制策略下输出的有功功率波动、无功功率波动、电流相对不平衡度与理论分析的结果基本相同，且电流有效控制在峰值电流以内，证明了所提控制策略的有效性。