新能源电力系统功角稳定分布式决策控制模型

2022-04-19朱灵子翟勇马覃峰唐建兴袁小清姚瑶

可再生能源 2022年4期

朱灵子，翟勇，马覃峰，唐建兴，袁小清，姚瑶

（1.贵州电网有限责任公司电力调度控制中心，贵州贵阳 550000；2.北京科东电力控制系统有限责任公司，北京 100192；3.贵州大学电气工程学院，贵州贵阳 550025）

0 引言

随着2030年“碳达峰”和2060年“碳中和”战略目标的提出，风电、光伏等新能源发电装机容量占比将逐步提高，电力系统将呈现高比例可再生能源和高比例电力电子特性[1]～[3]。由于新能源发电与常规机组的出力特性不同，因此在系统中大量常规机组被风电和光伏替代的同时，系统的功角稳定特性也将发生变化，这使得新能源电力系统功角稳定性分析的难度大大增加[4]～[6]。另外，可再生能源出力具有较强的波动性，一旦发生大扰动，将使电力系统无法实现同步协调，导致功角失稳。深入分析新能源电力系统下的功角稳定性，研究系统发生故障后功角振荡中心定位、辨识以及控制方法，将会为电力系统的安稳运行提供科学依据。

国内外对于电网安全稳定的控制决策已经开展了大量的研究，并取得了一些成果。文献[7]、文献[8]提出了在线稳定评估系统的架构，介绍了辅助决策在其中的位置和作用。文献[9]介绍了互联电网预决策系统中预防控制和紧急控制一体化框架以及与其它系统的接口。文献[10]提出了基于数值积分灵敏度和梯度的快速切机切负荷方法。文献[11]、文献[12]提出了基于轨迹灵敏度的暂态安全域分析方法，建立了基于安全域的暂态稳定紧急控制模型。文献[13]将控制决策作为一个非线性规划问题，提出了基于EEAC稳定裕度指标的控制措施搜索方法。文献[14]利用发电机功角变化情况，将系统等值为两个机群，逐步调整两侧功率并确定控制方法。

针对电力系统暂态稳定和动态稳定过程中存在的功角稳定问题，本文首先分析了电力系统同调机组群的振荡特性，对振荡中心进行定位。根据动态过程中各个振荡区域的动态特性，结合实际工程中确定控制措施的经验，确定可调整区域和控制设备。针对新能源发电与常规机组的出力特性差异，分析了新能源接入后系统的功角稳定性。在此基础上，建立新能源电力系统分布式能量最优控制模型。通过仿真验证了本文所提模型的合理性，该模型能够提高功角稳定控制精度。

1 功角振荡中心定位与可调区域识别

本文以电力网络结构识别为基础，对系统发生暂态及动态发电机功角失稳后系统的振荡机组群和振荡中心进行识别。基于机组的摆动特性识别可调机组，为实现功角稳定控制奠定基础。

本文提出的功角稳定辅助决策方法包含以下几个步骤。第一，进行基础数据处理。基础数据包括潮流数据、稳定数据、故障数据和断面定义数据。第二，进行单故障处理，即针对每个故障分别进行处理，其中考虑多个故障的影响对单个故障进行修正。第三，确定可调机组，对联络线、振荡中心线路以及电压等级等进行拓扑分析，确定可减少机组出力和增加机组出力的区域，寻找可调的发电机组，确定可调机组的顺序。第四，进行功角稳定控制。综合所有故障可行的调整措施，结合考虑所有故障后系统的拓扑分析，对各机组功角进行分布式控制，并检验控制措施对故障修正的有效性。

1.1 振荡中心定位

振荡中心的位移函数如下：

振荡中心在系统外时，m不在[0，1]内。且存在ωi<ωB或者ωA<ωi。

1.2 可调区域识别

可调区域是可以采取措施的部分，包括可增加出力的区域、可减少出力的区域。可调整区域识别基本步骤如下。

步骤一：采用振荡中心对网络进行分割

首先从电网本身物理特性对电网进行分割，利用振荡中心的特性对网络进行分解，可以识别出电网在特定扰动后的同调区域。图1是一个基于振荡中心进行网络分割的示意图。

图1 基于振荡中心的网络分割Fig.1 Network division based on oscillation center

图1中有5个电网互联成为一个较大的互联电网。假定故障发生在系统3，在动态仿真过程中检测到3个振荡中心，则将系统分解为4个振荡区域。实际系统振荡中心通常出现在较弱的联络线上，特别是在不同地区之间的联络线上，但也可能出现在一个地区电网内部连接比较薄弱的区域，如图1中的振荡中心1。发生多个故障时，可能出现更多的振荡中心，则网络将会分解为更多的区域。

步骤二：考虑人为指定的断面对电网进行分割

对于较大的互联电网一般会包含多个稍小的电网。考虑到不同区域电网的管理范围不同，实际电网采取控制措施，通常须要在本管理范围之内进行。因此，在控制措施自动决策中，必须考虑故障发生的地区和采取措施区域的关联关系，须要在振荡中心的基础之上叠加管理范围条件，对整个网络进行分解。系统中可能存在非常关键的断面，对系统稳定性影响比较大。

假设图1中的系统1，2，3，4，5都由不同区域电网管理，考虑到管辖范围，将系统进一步分解为6个区域，如图2所示。

图2 基于管理范围和振荡中心的网络分割Fig.2 Network division based on oscillation center and management

步骤三：确定可调整区域

辅助控制须要给出运行方式预先调整的建议。为了保持功角稳定，通常采用降低输电断面功率的方法，即降低送端发电机出力、增加受端发电机组出力。因此须要确定送端、受端两侧可调整区域。

步骤四：确定考虑多个故障的最终可调整区域

在含有多个故障情况时，送端和受端网络的确定比较复杂，按照上述方法确定的可调整网络可能存在重叠或者冲突，须要进一步考虑多个故障之间的关联关系，去除重叠区域。

在图3所示的网络中，假设系统5发生故障，在子系统5和系统5之间出现振荡中心。图3是根据振荡中心和管辖区域所划分的网络分割示意图。

图3 系统5故障对应的网络分割Fig.3 Network division for system 5 fault

同时考虑图2和图3两个故障对应的可调整区域，两者存在重叠和互斥的区域。此时基本上保留振荡明显的区域，受端可调整区域适度减小。如图4所示，同时考虑两个故障后的送端区域为区域2，3，41，受端区域为区域42。

图4 考虑多个故障的网络分割Fig.4 Network division for multi fault

2 新能源接入的系统功角稳定特性分析

考虑到新能源发电与常规机组出力的特性不同，在新能源系统渗透率逐步提高的同时，系统的功角稳定特性也将发生变化。根据传统电力系统动态分析，风电接入前多机系统的转子运动方程为

式中：Ei，Ek为节点i，k的电压；δS，δR为机群S和机群R的功角；Gij，Bij为节点i，j的互导和互纳；Pm为系统机械功率；Pmax为系统电磁传输功率的最大值；MS，MR为S，R机群的转动惯量系数。

风电接入系统后，根据节点导纳矩阵，得到计及风电影响的转子运动方程：

可以看出，式（8），（9）是通过将暂态过程中风电机组外特性对系统同步机电气联系的影响，折算到等值系统的机械功率上，可实现对新能源系统的暂态功角稳定分析。

3 新能源电力系统分布式决策控制模型

考虑N个区域电网参与控制，其中第i个机组的状态变量记为si（t）=（x，y，νx，νy）T，能量控制输入为u（t）=（ux，uy）T。每个区域电网视为二维平面内的质点，其能量控制特性可表示为

暂态过程中，表征系统的各种电磁参数都会发生急剧变化，使发电机的电磁功率和机械功率之间失去平衡。接入风电后，虽然风电本身不存在功角稳定问题，但是会改变系统的电磁暂态过程，从而影响发电机转子运动暂态过程。所以，可以通过能量函数的方法实现对系统的功角稳定控制。定义系统能量函数Vi[ui（t）]=uiT（t）Riui（t），Ri为正定矩阵。可再生能源电网的最优能量控制可描述为给定初始状态S0以及暂态过程的时间T∊Z，控制输入向量ui（0），…，ui（T-1），使得Zi（T）=1-Δθi，同时最小化功角振荡，其中Δθi是功角相对于初始状态的改变量，功角稳定最优控制模型如下：

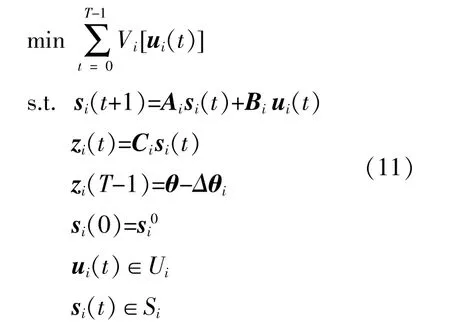
式中：Vi[ui（t）]为系统的能量函数；si（t）为第i个机组的状态变量；zi（t）为系统的输出变量；A，B，C为辅助参数。

可再生能源电网的运行状态与能量控制均须满足稳定性约束，即对任意t∊[0，T]，都有-si（t）∊Si，ui（t）∊Ui。利用线性不等式的方法对稳定性约束进行处理。

4 算例分析

以某地电网实际数据为算例，区域电网1和区域电网2间为可再生能源汇集区。以互联电网两种极限故障进行仿真，验证本文功角稳定控制方法的有效性。互联电网基本结构如图5所示。

图5 互联电网基本结构Fig.5 Basic structure of interconnected power grid

该互联电网主要由区域电网1～5组成，并与区域电网6相连。其中区域电网3是主要的受电区域，区域电网1,4除了是主要送电区域之外，还与部分电厂直接相连。该电网存在的主要问题是区域电网1外送存在低频振荡问题，故障比较严重时可能会引起功角失稳。因此，以区域电网1外送作为主要的研究目标，分析本文中提到的方法，并验证其有效性。图6为区域电网1与区域电网2的连接结构示意图。

图6 区域电网1与区域电网2的结构Fig.6 Connection structure of regional power grid 1 and regional power grid 2

选取比较严重的两个故障形式。故障1：5-6双回线路三相短路，0.1 s跳双回；故障2：4-5双回线路三相短路，0.1 s跳双回。

①进行暂态稳定计算，确定振荡中心

两个故障计算结果都发生了功角失稳，统计的振荡中心如表1所示。

表1 振荡中心统计表Table 1 Statistical chart of oscillation center line

同时统计动态过程中的功角波动和电压波动作为后续发电机排序的重要指标。发电机功角波动为所有时刻功角相对于初值的差值绝对值之和，电压波动为所有时刻发电机高压侧母线电压相对初值的差值绝对值之和。

②根据振荡中心和联络线确定可调整区域

根据互联电网的网络特点，指定联络线如图7所示。

图7 指定联络线示意图Fig.7 Specified link schematic diagram

结合振荡中心和联络线数据可以将系统分为如图8所示的多个区域。故障1发生时，可降低出力区域为区域电网1，可增加出力区域为区域电网2和3；故障2发生时，可降低出力区域为区域电网1，可增加出力区域为区域电网2和3。由于可再生能源汇集在两个故障控制措施中，其功能定位是矛盾的，不对其进行调整。

图8 基于振荡中心和联络线的可调区域Fig.8 Adjustable area based on oscillation center and link

③确定可调发电机及其顺序

针对选取的两个故障，可根据发电机动态过程中出力区域的发电机端电压变化量和发电机相连电压等级来确定顺序。由于故障发生在500 kV电网，因此优先考虑500 kV电网直接相连的发电机。故障1对应的可降低出力发电机及其排序如表2所示。故障2与故障1基本一致，不再列出。

表2 故障1可降低出力发电机Table 2 fault one generator list output can be reduce

可增加出力发电机基本采用上述类似的方法来确定，优先考虑500 kV直接相连的发电机。故障1对应的可增加出力发电机如表3所示。由于发电机较多，仅列出前10组。故障2与其类似，不再列出。

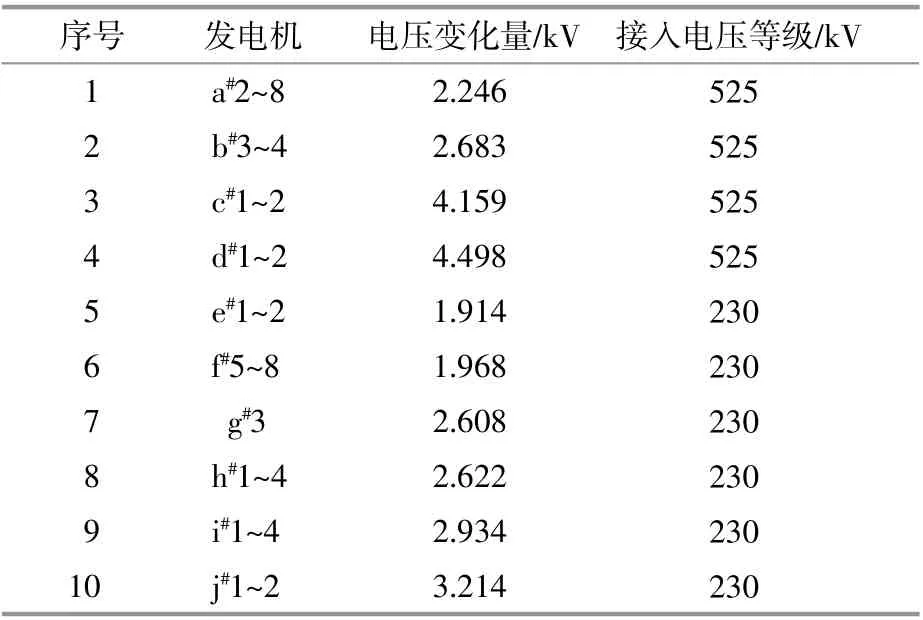
表3 故障1可增加出力部分发电机Table 3 fault one Generator list output can be increase

④确定可行的调整控制措施

在表2和表3的基础之上进行发电机组合。先确定可调整的功率范围以减少组合数，然后确定组合，并采用时域仿真计算，确定可行的调整方法。针对选取的两个故障，首先分别进行计算，然后再组合进行计算校核，最终确定适应两者的可行调整控制方法。对于每组故障都可以给出多种发电机组合措施。表4给出了故障1和故障2的一组可调整控制措施。

表4 故障1和故障2的可调整控制措施Table 4 adjustable control methods for fault one and two

表4中，故障1的调整措施量比较大，涉及到的发电机较多，而故障2调整措施量相对较小，涉及到的发电机较少。在上述措施基础上须加以综合考虑，得到对于两个故障都可行的调整措施。由于两者的可调整区域具有一定的重叠性，因此首先以故障1措施作为基准，校核对故障2的有效性；如果无效，则增加故障2的部分措施继续进行校验。最终结果表明，若故障1的措施对故障2有效，即将故障1的措施作为最终的有效措施。