基于分组密码的网络数据保形加密数学模型
2022-04-19张育梅
张育梅
(长春工业大学人文信息学院,吉林 长春 130000)
1 引言
保形加密即数据脱敏的一种形式,数据脱敏就是通过一些特殊的处理,使数据信息处于一种变形的情况,避免入侵者从脱敏处理后的数据中得到任何有关于用户的隐私信息,进而保护用户的个人信息安全。在金融、电信、电力与医疗等行业中,数据脱敏技术具有很好的应用前景,例如,在网络系统维护中,数据具有较多关键性隐私数据,一旦遭到泄露,就会被不法分子使用,分析用户的行为等,所以在传输、储存与共享时就需要对数据进行脱敏处理。
凭借数据脱敏结果,把其分成两种类型:可恢复类与不可恢复类。可恢复类即脱敏系统对隐私数据在进行处理之后,通过某个指定的形式将处理后的数据恢复到起始数据的状态,其能够依靠加密解密算法当作处理模型;不可恢复类即凭借脱敏系统对隐私数据在进行处理之后,没有任何方法能够将其复原。不可恢复类脱敏主要是应用到数据共享与公开上的,而可恢复类就可以作用静态传输与动态储存上。因此,可恢复类数据脱敏方法更加优越。可恢复类中存在一种代表性的保形方法,该保形方法能够同时让密文与源文以数据的形式存在。
关系型数据库的产品和脱敏技术不能直接应用在新兴的网络平台,虽然保形加密已经比较成熟,但是将这种方法直接作用在网络平台上还是较为少见的,并且如果直接将保形加密算法作用在网络数据中,可能会出现数据无法复原或数据崩溃等问题。
针对上述问题,提出了一种基于分组密码的网络数据保形加密数学模型。
2 基于分组密码的数据保形加密数学模型
2.1 分组密码的优化加密函数
设定网络数据明文分组内一共存在N种小块,就是M=(m0,m1,…,mn…1),其中mi∈{0,1,…,N-1}。分组密码的加密函数为
ci=EKEi(mi)≡(mi+ki)modN
(1)
式中,加密秘钥是KE=(k0,k1,…,kN-1),k1∈{0,1,…,N-1}(i=0,1,…,N-1)。
通过感知器构建的分组密码[1],需要k0,k1,…,kN-1互补相同,就是k0,k1,…,kN-1即模n的冗余集。假如这种方式成立,反而会减少密码分析者攻击空间,即让密码逐渐失去安全性,只要(k0,k1,…,kN-1)∈{0,1,…,N-1}N,就是在i≠j时,ki=kj(i,j=0,1,…,N-1)也可以建造出对应的[2]解密函数,同时将分子者攻击的穷举空间进行扩展,即将密码的安全性进行了增强。该分组密码的解密函数能够通过下式描述
mi=DKDi(ci)≡(ci+N+(-ki))modN
(2)
式中,加密秘钥与解密秘钥都是[3]相反数,就是KD=(-k0,-k1,…,-kN-1),ki∈{0,1,…,N-1},(i=0,1,…,N-1)。
混乱与扩散就是隐蔽明文数据冗余的的一种形式。由于模运算就是一种非线性的运算,所以加密函数与解密函数能够提取出一定量的混乱特征[4],但是加密函数与解密函数的扩散特征就不是非常明显了。
设定明文分组一共存在N种小块,就是M=(m0,m1,…,mn…1),对应的密文分组也存在N种小块,就是C=(c0,c1,…,cN-1),其中,mi∈Z,ci∈Z(i=0,1,…,N-1)。
优化加密函数是
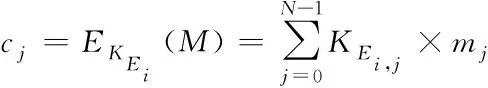
(3)
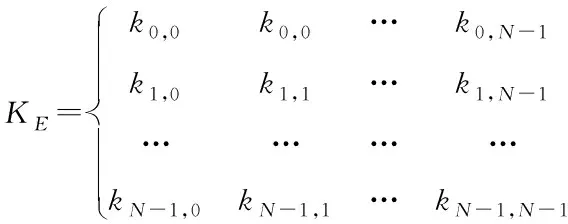
对应的解密函数是
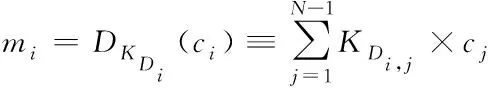
(4)
式中,加密秘钥和解密秘钥都是逆矩阵,就是KD=(KE)-1。
结合上述来说,加密函数与解密函数的扩散特征是非常明显的[5]。
2.2 网络数据保形加密系统
因为上述两种密码系统可以凭借乘积的方法被融合在一起。凭借这种概念,能够将上述两种模型作为两种密码系统T与R,将两种密码独一作用至一层前馈神经网络中,通过乘积的形式就可以取得一种同时满足混乱与扩散规则的网络数据保形加密系统[6],其系统结构如图1所示。
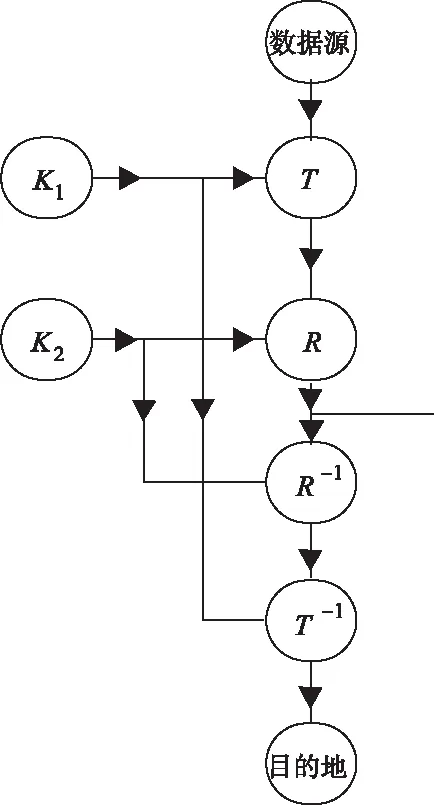
图1 网络数据保形加密系统结构图
通过图1能够看出,T的密文空间与R的明文空间是同样的,因此可以依据T系统进行加密,然后对加密过程的结果利用R系统进行处理。
在第一层加密系统T内,因为每一种神经元都是输送函数的模运算,而模运算就是一种非线性的运算形式,在第二层的加密系统R里,也能够凭借矩阵相乘的运算方法[7],所以该模型在整体上能够描述出很好的混乱特征。
在第二层的加密系统R里,由于利用该层输入向量与神经元之间的链接权值矩阵作为加密秘钥K2,所以这一层能够很好的描述出扩散特征。从理论上可以描述为,融入至加密秘钥K1与加密秘钥K2没有出现变化时,更改明文向量的随机一种元素[8],加密之后就可以使N种密文出现变化,而调整随机一种密文元素,在进行解密后也可以让N种明文元素产生转变,所以明文与密文之间的扩散干扰强度是非常高的。
同理,在加密秘钥与明文K2没有出现变化时,调整加密秘钥K1的随意一种小块,在加密之后可以使N种密文小块出现变化,在加密秘钥与明文K1没有出现变化时,调整加密秘钥K2的随意一种小块[9],加密之后可以让一种密文小块产生转变,所以密文对秘钥的扩散干扰强度也是非常高的。
针对加密秘钥K2来说,假如ki,j(i,j=0,1,…,N-1)随机挑选,只要(k0,k1,…,kN-1)∈{0,1,…,N-1}N即可,因此就存在NN种不同的挑选方式[10]。在密码分析者使用穷举秘钥空间进行攻击时,只需要取N种足够大的值,密码分析者只靠穷举NN种秘钥来运算加密秘钥[11],或是通过加密秘钥加密的新密文与同种加密方法,运算其对应的明文在理念上是不可能的,即这个系统在运算上是较为安全的。
对于加密秘钥K2来说,假如ki,j(i,j=0,1,…,N-1)随机挑选,只要ki,j∈R同时KE与KD是相互可逆的即可。因此,在密码分析者使用穷举秘钥空间攻击时,只靠穷举秘钥空间计算加密秘钥,或是通过同一种加密算法与加密秘钥的新密文计算器相应的明文来得到明文是不可能的,所以这个系统是一种无条件安全的。
从整体上来看,在密码分析者凭借穷举空间进行入侵时,由于需要穷举加密秘钥K2与加密秘钥K1的密钥空间,而在理念中加密密钥含有无穷个收集算法,所以只利用穷举密钥空间运算在正常情况下是不会出现变化的,即这个分组密钥在理论上是安全的。
2.3 网络数据保形加密数学模型
为了并行支持数字、纯字母与纯数字混合的加密处理,对NIST标准草案的FF1模型进行微调。在设定分组加密秘钥K基数n和tweak值T时,FF1模型对明文P进行加密,设定n=10里的字符集对应的数字即0~9,再向上提升就是相应的英文字母a~z,加入16进制相应的字符集是{0,1,…,9,a,b,…,f}。在设定出FF1模型的基础上简单微调保形加密整体流程。
模型依据基数n的设定来微调所提供支持的字符集,n的取值范围是{1,2,3,…,10,26,36}。举例描述,n=10即加密数域,该数域是十进制数,就是字符集的数字,n=36即加密数据,这个数据是三十六进制数,通过上述信息支持字符集是英文字母与数字的混合[12],而为了供给纯英文字母字符集的加密,能够让n=26,此时源对应的字符集即0~9、a~p,因此加密前后进行附加处理,将数值转化为a~z。该模型是不会区分字母的大小写的,但是能够对其进行拓展,即能够把同时存在字母大小写和数字的字符集作为六十二进行数,对应字符进行处理,同样的,继续拓展进而供给更大的字符集,比如ASCII字符。为了让这种字符更加简单。
FF1模型以多种模式对数据进行加密,针对不同情况下,该模型以三种模式呈现,即简单单机模式、ETL工具模式、Spark并行模式。具体如下所示:
1)简单单机模式
简单单机模式即三种模式里较为简易与直接的系统,其思想即把储存在网络平台上的数据线导至本地内存里,在对储存在本地文件里的网络数据依靠保形加密方法对其进行处理,从而实现网络数据的脱敏。依靠储存管理形式的不同,利用了相应的网络编辑接口来支持HDFS文件数据的导出。之后在单机上依据上述方式加密网络数据。
简单单机模式的好处就是直观与简易,同时能够在脱机运行,但其缺点也比较明显,因其只是依靠单机的方式对网络数据进行加密处理,因此这就导致了这种方法在处理脱敏时效率较慢。
2)ETL工具模型
为了提高加密的速度,可以利用ETL工具来提升并行度与流水线的运作效率。依据开源的ETL工具,把保形加密依靠转换插件的形式来供给,进而直接提供网络平外内的多种数据模式。Kettle就是一种跨平台的开源ETL工具,这种工具可以直接让用户依靠可视化工具来对现实数据导入与导出,同时该工具还能够运行多个发行版本。
保形加密插件的开发以交互界面加密模式为主。交互界面的运作即与用户之间的交互行为,并为用户的参数配置提供一些帮助,存在明文列名、密钥配置、tweak配置与密文列名等。依靠于Kettle来处理保形加密的转换插件配置与主界面的转换系统,也就是ETL工具模式里含有的一种优点。相对来说,其它的量化方式能够完成的只是通过终端参数的指示对数据进行一种简单的交互操作。
ETL工具模式可以对保形加密的效率进行提升,而其原因存在两种。第一种就是加密脱敏、结果储存与数据导出,通过三条而组成的流水线,能够对数据进行迭代脱敏处理,之后在传送至标定的坐标。第二种方法即供给并行处理,在Kettle的单机运行模式里,能够拟定保形加密转换流程的并发数,进而通过多核心处理器对网络大数据进行保形加密,Kettle还能够形成集群模式,能够把数据分发至集群的每一种逐级内,完成多逐级并行处理,缩短加密运行时间。
3)Spark并行模式
为了充分显示分布式储存和并行化运算的优势,利用并行估算框架来完成保形加密的操作。先对比Spark并行模式,依靠内存估算将输入操作与硬盘输入的效率提高,进而提高估算的效率。因此,基于Spark的并行模式可以对保形加密效率最大承受度的提升。
依据Spark的编程接口对网络数据加密脱敏处理流程为:首先,读取网络储存库内的数据信息,从而,形成Spark的单行分布与抽象的数据集,之后,在利用数据Spark支持的并行估算编程接口,在集群内对RDD进行加密处理。
在这种模式内,保形加密即依据Spark作业的形式来体现其效率的提升,把其传输至分布式计算机里来实现运行,从而实现网络数据脱敏。因此,对于Spark的参数调优对于该模式的运行速度具有促进作用。
通过上述能够表明,根据不同的数据环境所需的处理效率与处理质量,三种保形加密模式针对实际情况进行自动切换。
3 仿真证明
仿真环境为Intel Celeron Tulatin1GHz CPU和384MB SD内存的硬件环境和MATLAB6.1的软件环境。
为了证明所提方法的实用性,将网络数据分为三次参数样条即两种自由端与夹持端,三次样条曲线在小绕度的状态下,效果较好,在绕度较大时,数据样条曲线和现实曲线就会出现较大的误差。而三次数据参数样条能够较好的解决大绕度的困难,如图2所示。
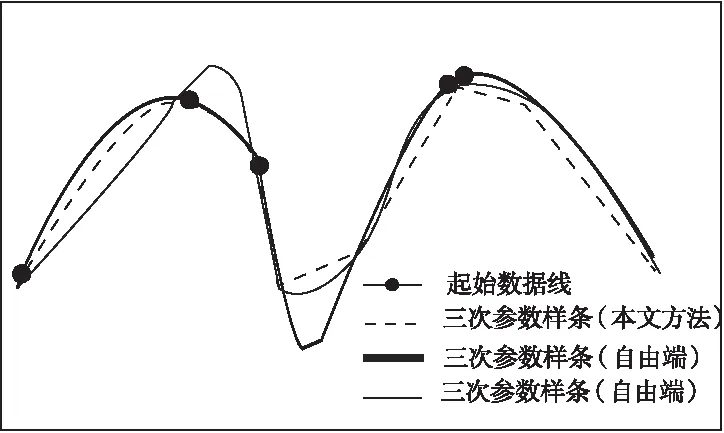
图2 三次样条和残次参数样条比对图
从整体的趋势上来看,三次参数样条在三个边界条件内,边界条件挑选所提方法效果较好,所以在对等高线内点进行保形加密时使用所提方法进行加密。加密之后的效果如图3所示。
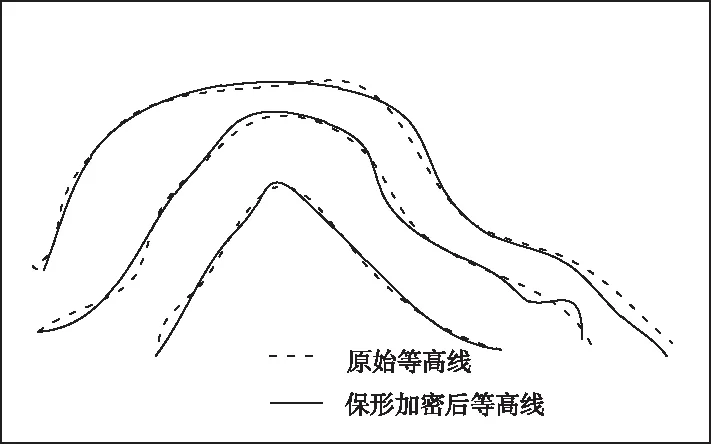
图3 等高线内点保形加密效果图
通过图3能够看出,使用所提方法保形加密之后的曲线不会出现和初始等高线太大的误差,因此证明,所提方法能够有效的对网络数据进行保形加密,并且加密之后不会存在太大的差异。
在此基础上,在执行保形加密过程后,对所提方法的加密性能进行测试,检测其速度和运行速度是否在最优范围内。实验结果如图4所示。
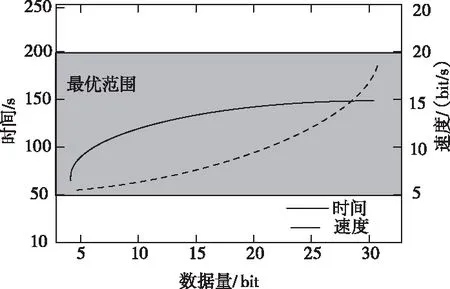
图4 保形加密后数据性能测试结果
如图4所示,在不同数据量的情况下,经过所提方法保形加密后,数据的运行时间和速度均在最优范围内,符合实际需求,实际应用性较好。
4 结束语
提出了一种基于分组密码的网络数据保形加密数学模型,仿真结果证明,在网络数据保形加密内,所提方法能够有效的对网络数据进行保形加密,并且加密之后不会存在太大的差异,并且经过保形加密后,数据性能较优,加密效率较高,加密之后与源数据差异较小。
