辨明方向 走出误区

文／葛亚美

同学们在复习平行四边形这块知识时，经常会在哪些知识点上出错呢？今天，老师整理了一些常见问题，希望能带同学们走出误区。

一、对性质理解不清

例1如图1，E是平行四边形ABCD的边AD的中点，CE与BA的延长线交于点F，若∠FCD=∠D，则下列结论不成立的是（ ）。

图1

A.AD=CFB.BF=CF

C.AF=CDD.DE=EF

【错解】A。

【错因分析】对相关性质理解得不够透彻，而且题目要选的是“不成立”的，凭感觉选择了一个答案。

【正解】∵ABCD是平行四边形，

∴AD=BC，∠B=∠D，AB∥CD。

∵BF∥CD，∴∠F=∠FCD，∠FAE=∠D。

∵AE=ED，∴△AEF≌△DEC，

∴AF=CD，EF=CE。

∵∠FCD=∠D，∴CE=DE，

∴DE=EF。故C、D都成立。

∵∠B=∠D=∠F，则CF=BC=AD。故A成立。

没有条件证明BF=CF。故选B。

【点评】此题考查了平行四边形的性质，即平行四边形的对边平行且相等，对角相等。

二、对图形的画法考虑不周全

例2在面积为15的平行四边形ABCD中，过点A作AE垂直于直线BC于点E，作AF垂直于直线CD于点F，若AB=5，BC=6，则CE+CF的值为（ ）。

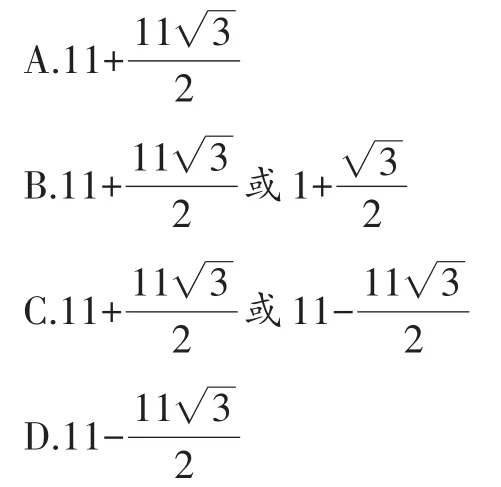
【错解】A。

【错因分析】此题有两种情况。

【正解】∵四边形ABCD是平行四边形，

∴AB=CD=5，BC=AD=6。

①如图2，过点A作AE⊥BC，AF⊥DC，垂足分别为E、F。

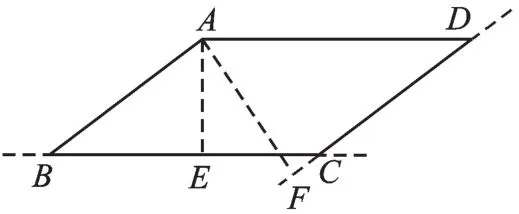
图2

由平行四边形面积公式，得BC×AE=CD×

在Rt△ABE和Rt△ADF中，由勾股定理，得的延长线上，

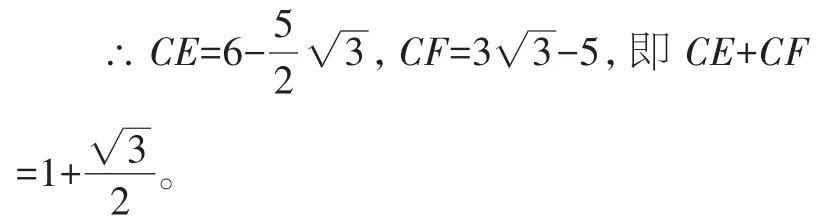
②如图3，过点A作AF⊥DC，AE⊥BC，垂足分别为F、E。

图3

由①知

在△ABE和Rt△ADF中，由勾股定理，得

【点评】本题考查了平行四边形性质、勾股定理的应用。对于没有图形的几何题，同学们尤其要注意多种情况的出现。

三、图形变换能力不强

例3如图4，将一张等腰直角三角形纸片沿中位线DE剪开后，可以拼成的四边形是（ ）。

图4

A.矩形或等腰梯形

B.矩形或平行四边形

C.平行四边形或等腰梯形

D.矩形或等腰梯形或平行四边形

【错解】B或C。

【错因分析】对于图形三种变换的想象能力偏弱，分析不出对应的图形。

【正解】如图5，若把△ADE绕点E顺时针旋转180°可得矩形；如图6，若把△ADE向下平移AD个单位长度，再沿BD翻折，可得等腰梯形；如图7，若把△ADE绕点D逆时针旋转180°可得平行四边形。故选D。

图5

图6

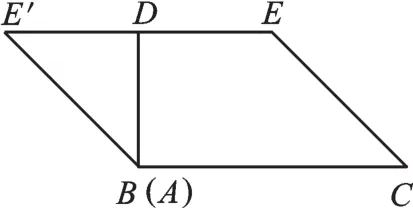
图7

【点评】本题考查了同学们动手操作的能力，让相等边重合即可很快得到答案。