对钢琴调律 若干基本问题的分析(上)
2022-04-19华天礽
华天礽
关于拍
拍(英:beat)是钢琴调律中最基本的听辨工具,是我们在调律中赖以分律、听辨同音弦组的唯一听觉依据。对于钢琴调律来说理解拍的形成机理,是很重要的。只有理解拍的形成机理,才会理解为什么我们要依靠拍和如何理解拍所表示的意思。
从音乐声学的原理来说,拍是声音干涉所产生的一种现象。频率稍有差别(10Hz以下)的两列波,在同一介质中传播时,会以不同的方式发生干涉。在两波通过的介质中的任一固定点上,波的叠加给出一个具有振幅随时间变化的特征的波。这个合成波的振幅随时间作周期性的变化。这种振幅的波动称为拍。当干涉的频率是可听声时,振幅的变化或拍,可由响度的变化来认别。每秒拍的次数等于两个分波的频率的差①。
例如我们听到两个纯音,一个100Hz,一个102Hz,同时传到我们耳朵,这样我们就会听到一个每秒有2次振幅(即音量)变化的拍,此时我们听到的由两个音融合而成的合成波的实际音高是101Hz。
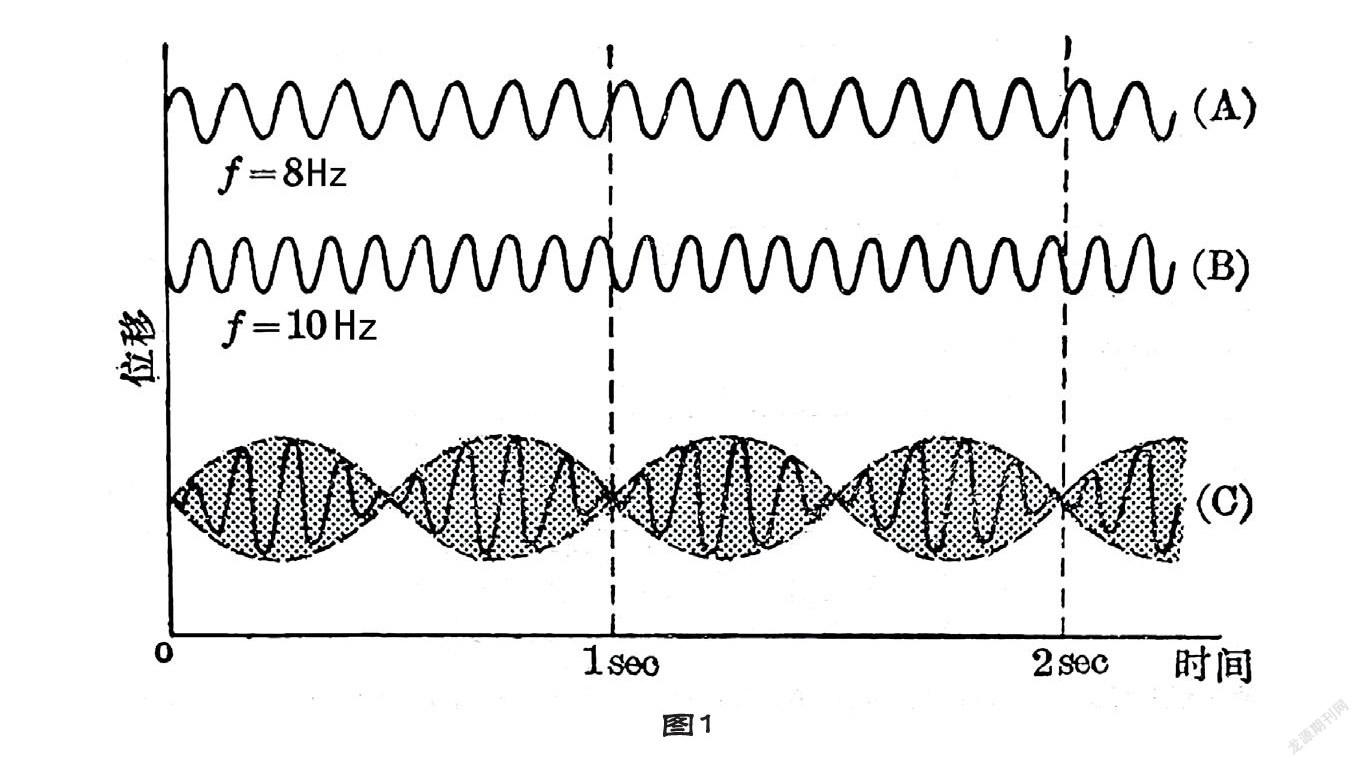
我们可以用图1②来解释拍形成的原因。图中(A)是8Hz的振动,(B)是10Hz的振动,当它们同时在空气中传播时,我们可以看到(A)的第三个波峰和(B)的第三个波峰几乎同步,两个波峰互相叠加,这样就形成相长干涉,合成为(C)的第一个波峰;而(A)的第四个波谷与(B)的第五个波峰也几乎同步,波谷和波峰互相抵消,这样就形成相消干涉,合成波的振幅几乎为零,合成为(C)中的波节。这样的现象在1秒钟内重复2次,产生合成波(C)每秒2次振幅变化的拍。而此时合成波(C)本身的频率为(8+10)/2=9(Hz)。
所以我们可以看到,拍实际上是由于两个音的振动,在传播中由于相长干涉和相消干涉交替出现而产生的合成波的振幅变化。
为什么两个音的频率差在10Hz以下,我们才能感受到拍呢?这是因为当拍在10Hz以下时,我们的听觉是能感受到实际振幅(音量)变化次数的;而当拍在10Hz以上时,我们的听觉已很难感受到实际振幅变化的拍的次数,而只是感到音色粗糙。
由于拍精确地反映了两个音之间的频率差,所以在音乐中当我们需要精确调节两个音之间频率差的时候,对我们的听觉来说,拍就几乎是唯一一个最重要的工具。
要注意的是,当我们听到两个频率稍有不同的纯音产生拍时,此时听到的合成音的音高是这两个纯音音高的平均音高,其频率为(f1+f2)/2。这个合成音称为“融合音”(英:fused tone)③。因为根据听觉理论,此时我们的听觉已无法分辨这两个不同的音高,只能听到一个融合音。当然对我们的听觉来说更明显的是这个融合音振幅变化的拍,而拍的频率是这两个纯音频率之差。
有些人聲称在钢琴调律中存在“正拍”和“负拍”,即440Hz和442Hz产生“正拍”;440Hz与438Hz产生“负拍”,这种看法是值得商榷的。从音乐声学的理论来说,拍不存在“正”“负”之说,拍只有一种,它只表示两个音之间的频率差,以振幅变化的方式呈现。上述这两种情况都会产生每秒2次振幅变化的拍,这种拍没有差别;差别在于前者我们听到融合音是441Hz,而后者我们听到的融合音是439Hz。
钢琴调律中产生拍的原理
根据音乐声学的原理,拍一般只会在两个纯音的频率差在10Hz以内时,才会产生,当两个纯音的频率差大于10Hz时,我们的听觉已无法分辨具体的拍频次数,而只会感觉到这两个音很粗糙。而在钢琴调律分律时,通常使用的四、五度,其频率差远远大于10Hz,那么此时的拍是从何而来的呢?
答案是,它们之间的拍产生于两个复合音之间的泛音列。例如纯五度的频率比是3:2,如果我们上方音的频率的基音是300Hz,那么下方音的频率的基音就是200Hz。根据声学原理,复合音中所有的泛音都与基音频率成整倍数关系,那么此时上方音的第二分音300×2=600Hz,下方音的第三分音200×3=600Hz,这样600Hz就是这两个复合音共同的分音频率。如果这个频率有差别,就会产生拍,这也就意味着这两个音的基音不是完全的3:2的纯五度。
我们以钢琴调律的实际例子来分析。根据十二平均律:A3的频率是220Hz,E4的频率是329.6Hz,此时,A3的第三分音是220×3=660;E4的第二分音是329.6×2=659.2,此时在660Hz与659.2Hz之间就会产生每秒0.8次的拍。这就是钢琴调律五度拍产生的原因。
那么是否可能发生拍的频率是正确的,而音的频率是错误的情况呢?从理论上来说是可能的。即当一个分音为660Hz,而另一个分音为660. 8Hz的时候,也会形成每秒0.8次的拍,但此时E4的频率就是660.8÷2=330.4Hz,而不是正确的329.6Hz。
那么这种情况我们的听觉能够分辨吗?从理论上来分析,我们的听觉是无法分辨的。
从理论上来说,此时我们听到的拍频是一样的,即每秒0.8次,这个没有差别。唯一不同的是融合音:660Hz和659.2Hz这两个音我们听到的融合音是(660+659.2)/2=659.6Hz;而660Hz和660.8Hz这两个音我们听到的融合音是(660+660.8)/2=660.4Hz,这两个融合音的频率是不同的。但是从听觉理论来说,我们的听觉是无法分辨659.6Hz和660.4Hz这两个音之间的音高差别的。人的听觉辨别不同音高的能力,称为最小音高差辨别阈(英:Just Noticeable Difference, JND)。人的听觉系统对频率的相对分辨率(定义为jnd(f)/f)大体为5‰④。660.4Hz和659.6Hz的频率差是0.8Hz,这个频率差,已经小于我们的听觉能够分辨的阈值。所以,从我们的听觉来说,是无法分辨这两者之间的频率差的。换句话来说,以上两组音的差别,我们的听觉是无法分辨的。
由此给我们一个重要的启示是,在钢琴调律中,搞清调律的方向是很重要的,如果调律的方向错了,尽管拍的频率是正确的,但律可能是错的。94527D73-E5B2-4AA8-9796-5E26E8662E66
分律时是选择上五下四,还是上四下五?
在钢琴调律分律时,通常都会面临一个选择,即是采用上行四度下行五度的分律次序,还是选择上行五度下行四度的分律次序?有些人认为这两种次序是一样的,但我们仔细分析可以发现,这两种次序是有优劣之分的。
我们都知道,纯五度是702音分,而十二平均律五度是700音分;纯四度是498音分,而十二平均律四度是500音分。如果采用上四下五的次序,一般从A3开始调D4,我们先调纯四度,即498音分,此时的D4还偏低,还需要再调高2音分。从频率来说A3是220Hz,纯四度是4:3的频率比,此时D4是220×4/3=293.3Hz。而十二平均律的D4应为293.7Hz。如果D4为293.7Hz的话,那么它的第三分音293.7×3=881.1Hz应该与A3的第四分音220×4=880Hz产生每秒1.1次的拍。此时,应该把D4调高到产生1.1次拍,才是正确的。在实际操作时,我们往往需要把D4调得高于正确值,再往下调到正确的293.7Hz,这样调出的音高才较稳定。问题是往下调的时候,音高下行,既可能正好调到正确的D4第三分音881.1Hz,也可能音高下行过多,调到878.9Hz。因为在这两种情况下,拍频都是1.1次,而我们的听觉实际上无法分辨881.1Hz与878.9Hz的差别(即880与881.1产生的融合音与880与878.9产生的融合音的差别)。当然在此期间拍的频率会有从快→慢→无→慢→快的变化,这只有在调律中仔细听辨拍频的变化才能控制,或通过其它检验音程才可能发现。实际操作过程可描述为A3→D4(纯)→D4(偏高)→D4(正确)。在操作中要非常仔細地听辨拍频的变化,否则有产生误差(即调成878.9Hz)的可能。
在接下来下行五度的操作中情况也是一样的。即D4→G3,纯五度为702音分,此时G3偏低2音分,需要将其提高2音分,其实际操作过程是:D4→G3(纯)→G3(偏高)→G3(正确)。在此过程中,同样存在产生误差的可能。
而我们如果采用上五下四的次序,情况就稍有不同。如果A3(220Hz)往上产生纯五度(702音分),此时E4的频率为330Hz,而十二平均律E4应为329.6Hz,这样它的第二分音329.6×2=659.2Hz,应该与A3的第三分音220×3=660Hz产生每秒0.8次的拍。这样我们只需把E4往下调,产生0.8次拍就可以了。实际操作过程为:A3→E4(纯)→E4(正确)。比前述的操作过程少一步。更重要的是,这样操作,一般不会发生把E4的第二分音调为660.8Hz,产生0.8次拍的可能。因为这样需要先把E4调纯,再往上调。这种反方向操作的情况一般不会发生。
下行四度也同样如此。E4下行四度为B3,纯四度为498音分,调纯后意味着B3还要下调2音分,实际操作过程为E4→B3(纯)→B3(准确)。同样,这样也不容易产生误操作的可能。
注释:
①J.E.William, F.E.Trinklein, H.C.Metcalfe, R.W.Lefler: Modern Physics 上海师范大学《物理学》翻译小组译 上海:上海教育出版社,1975.9 第340页。
②同①,第341页。
③Juan G.Roederer: Introduction to the Physics and Psychophysics of Music, New York: Springer-Verlag, 1975, p.29。
④唐林,张永德,陶纯孝:音乐物理学导论,合肥:中国科学技术大学出版社,1991,12. 第216页。94527D73-E5B2-4AA8-9796-5E26E8662E66
