基于拉普拉斯算子的综合孔径辐射计成像算法
2022-04-18杨晓城杨真乙阎敬业蒋明峰
杨晓城,杨真乙,阎敬业,武 林,蒋明峰
(1. 浙江理工大学信息学院,浙江杭州 310018;2. 中国科学院国家空间科学中心,北京 100190)
1 引言
作为被动微波遥感领域的一项新技术,综合孔径微波辐射计利用小口径天线干涉综合成大口径天线的方法,有效提高了对地观测的空间分辨率,同时避免了大口径天线带来的折叠、机械扫描和重量等方面的困难. 目前,综合孔径微波辐射计逐渐成熟,被应用于陆地、海洋和大气遥感以及人体安检等领域[1,2].
成像反演是综合孔径微波辐射计的一项关键内容[3,4]. 然而,综合孔径辐射计成像反演在数学上是病态的反问题,需要进行正则化处理以获得稳定的唯一解. 目前常用的正则化方法可归为2 类:第一类是采用数学的手段进行约束,如Tikhonov 正则化、最小范数正则化、共轭梯度最小二乘(Conjugate Gradients Least Squares,CGLS)等[5~7];第二类方法是通过综合孔径辐射计自身的物理特性进行约束,即带限正则化法[8]. 虽然上述正则化方法能够有效克服其病态性,但依然存在较大的重构误差[9].
值得注意的是,传统的Tikhonov 正则化和最小范数正则化方法,将固定的约束信息添加到了所有的频带上,这会导致重构得到的亮温解过于平滑,从而无法保留原始亮温分布的所有特征. 因此,借鉴双参数正则化[10]的思想,本文通过在正则化过程中引入一项新的拉普拉斯算子项,提出了一种拉普拉斯混合正则化方法,并基于研制的L 波段FPIR 样机进行了仿真验证.
2 综合孔径辐射计成像原理
与真实孔径辐射计不同,综合孔径辐射计干涉测量结果是观测场景亮温分布在频率域上的可见度函数采样. 可见度函数V(u)与观测场景亮温分布TB(ξ)之间的关系可以表示为[11,12]
其中,ξ=(sinθcosφ,sinθsinφ)为在笛卡尔坐标系下方向余弦矢量,ukl为与天线k和l对应的基线矢量;Ωk和Ωl分别为天线k和l的等效立体角,Fk和Fl分别为天线k和l归一化电压方向图(表示Fl的复共轭);Tr为接收机的物理温度,kl(τ)为fringe washing 函数,τ=-ukl ξ/f0为时间延迟,f0为中心频率.
将式(1)进行离散化,并考虑实际测量过程中可见度函数测量误差和噪声的影响[13~15],可得
其中,G为系统调制矩阵,V为可见度函数向量,T为观测亮温向量,n为噪声向量. 由于亮温采样点数M一般大于可见度函数采样点数N,因此式(2)是欠定的. 同时由于G矩阵的不适定性,噪声n的微小变化都会使得反问题解产生很大的扰动,因此矩阵方程是病态的,其解既不唯一也不稳定.
对于病态的线性方程,通常是进行正则化处理. 正则化的作用是通过增加有关解空间的附加信息,并利用约束泛函获得稳定可行解,从而缓解反问题的病态性. 目前,综合孔径辐射计中广泛使用的是最小范数正则化和带限正则化方法.
最小范数正则化是指求解式(2)的最小范数解,即

为了求解式(3),先对矩阵G进行奇异值分解,即

其中,si≥0为G矩阵按降序排列的奇异值,向量ui和vi分别为si的左奇异向量和右奇异向量. 然后,通过抛弃那些对误差传递影响很大的较小奇异值来缓解矩阵G的病态性,即采用一个秩亏缺的良态矩阵Gk=来代替矩阵G. 因此,反演亮温为

其中,k为正则化参数.
对于综合孔径辐射计,由于天线单元数量是有限的,因此测量的可见度函数采样值被限制在有限的带宽H内. 带限正则化是指求解下列约束最小二乘问题:

其中,T′=UT为T的傅里叶变换,U是离散傅里叶变换运算符. 因此,反演亮温为

其中,J+=(J*J)-1J*是矩阵J=GU*Z的广义逆矩阵,Z是补零运算符,*表示共轭转置.
由于综合孔径辐射计覆盖的基线范围有限,无法获取观测目标亮温的高频分量,因此存在固有的系统误差. 为了降低系统误差,引入一个先验亮温分布,对差分可见度函数ΔV=V-进行反演成像,即求解最小二乘问题:

其中,ΔT=T-. 为了获得先验亮温分布,首先利用陆地与海洋分界的先验信息,将观测场景划分为陆地区域和海洋区域,并将每个区域的亮温设为恒定值,然后根据最小二乘准则求出每个区域的亮温值,详见文献[16]. 因此,对于最小范数正则化,其反演亮温变为

对于带限正则化,其反演亮温变为

为了方便区分,式(9)的方法称为改进的最小范数正则化,式(10)的方法称为改进的带限正则化.
3 拉普拉斯混合正则化
对于双参数混合正则化方法,王文娟等将其应用于电导率的反演成像中,得到了更为精确稳定的解[17];刘婷等将其应用于脑磁时序信号的逆问题求解中,重构出更为准确且时域平滑的脑内神经信号[18]. 受此启发,为了进一步降低综合孔径辐射计的重构误差,本文借鉴双参数正则化的思想,提出了一种拉普拉斯混合正则化方法.
3.1 拉普拉斯混合正则化方法
为了获取高精度的观测场景亮温,本文在标准的单参数Tikhonov 正则化的基础上,通过引入新的拉普拉斯算子项,对差分亮温添加2 种不同的约束,即求解如下极小值问题:
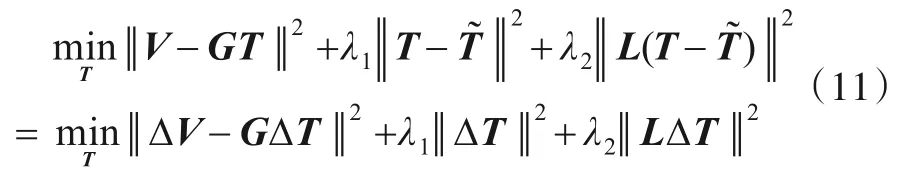
其中,‖ΔV-GΔT‖2为数据拟合项,即解的残差范数;‖ΔT‖2为能量泛函约束项,使得解全局能量最小;‖LΔT‖2为拉普拉斯算子项,使得重构解能够保留原始亮温分布的多尺度信息,其中L是离散化后与拉普拉斯算子对应的正则化矩阵;λ1和λ2为大于0 的正则化参数. 拉普拉斯算子可以分为一阶拉普拉斯算子和二阶拉普拉斯算子等,其中一阶拉普拉斯算子可以反映图像的边缘特征,二阶拉普拉斯算子可以反映图像的纹理结构特征. 本文采用二阶拉普拉斯算子,则离散化后对应的正则化矩阵L为

求解式(11),可得反演亮温为

3.2 正则化参数的选择
正则化参数的选取在综合孔径辐射计成像反问题研究中起着非常重要的作用. 然而,正则化参数的选取策略较为复杂而且没有普适的方法. 目前,主要采用的2 种方法,分别是L 曲线和广义交叉验证(Generalized Cross-Validation,GCV)准则.
对于最小范数正则化,将采用GCV 准则选取正则化参数.GCV 准则的基本思想[19]是当原始数据项V中去掉一项Vi时,由此产生的新方程可以预测出去掉的分量,即通过最小化GCV函数来确定正则化参数,其中f(k)=GG+k,tr表示方程的迹.

对于拉普拉斯混合正则化,其有2个正则化参数需要确定,通过传统的GCV准则无法同时得到最优的2个参数,所以本文采用多维扩展后的GCV准则. 多维扩展后的GCV 准则[20]将GCV 函数视为向量λ=(λ1,λ2)T的多元函数,即

其中f(λ)=G(G*G+λ1I+λ2LTL)-1G*. 然而,通过最小化式(15)求解正则化参数计算代价太大,难以同时处理矩阵G和所有正则化矩阵. 文献[20]证明了可以利用矩阵Z(λ)=(vi(λi))2来代替v(λ),通过求解目标函数Z(λ)的极小值来获取近似解. 其求解过程为分别对单参数的GCV 函数vi(λi)进行最小化获得正则化参数λ1和λ2,然后组成向量λ.
最小范数正则化和带限正则化等传统正则化方法对成像反问题添加单一的约束和限制,属于单一正则化方法. 然而,综合孔径辐射计成像反问题是非常复杂的,单一正则化方法都有一定的侧重性,具有相应的优点和缺点,这意味着即使在选择了最优的正则化参数情况下,单一正则化也无法确保反问题解的稳定性和健全性. 因此,与传统的单一正则化不同,本文提出了一种拉普拉斯混合正则化方法,其优点在于通过引入拉普拉斯算子项来反映原始亮温分布的其他尺度特征,如边缘特征、纹理结构特征等,从而提高反演亮温的精度.
为了降低频谱截断所导致的吉布斯振荡现象,一般需要利用窗函数对可见度函数进行加窗平滑,可得加窗后重构亮温为

其中,W为窗函数.
为了定量地分析重构误差,计算重构结果与真实亮温分布之间的均方根误差RMSE 与峰值信噪比PSNR,即

其中,m为无混叠视场内的像素个数.
4 仿真结果
为了验证上述拉普拉斯混合正则化方法的有效性,基于L 波段(1.4 GHz)FPIR 样机系统进行了仿真分析.FPIR 样机是一套L/X 波段一维全极化综合孔径辐射计,主要用于探测海表面盐度[21]. 图1为FPIR样机双频天线阵列布局,其中L 波段的阵列天线放置在两边,X 波段的阵列天线放置在中间区域. 仿真系统为工作在H 极化状态的L 波段FPIR 样机,最短基线为d=0.589λ0,6 根观测天线a1,a2,…,a6 稀疏地排列在不同的位置,其间隔依次序分别为d、d、2d、5d、d,所以可得最长基线为10d.

图1 FPIR双频天线阵列布局
仿真系统其他参数如下:带宽为B=20 MHz,fringe washing 函数设为sinc(Bτ),积分时间为1 s. 包含零基线并考虑共轭对称性后,总共可获得31 个可见度函数采样点. 在天线暗室中,对L 波段的阵列中6 根观测天线的方向图进行测量,综合孔径方向上测量的归一化天线电压方向图如图2所示.

图2 综合孔径方向归一化天线方向图
原始亮温分布如图3 所示,包括2 种典型的观测目标区域,其中图3(a)为纯海洋区域,图3(b)为海洋陆地交界区域. 原始亮温分布来源于Aquarius 卫星2013 年8 月19 日观测的某区域L 波段H 极化辐射亮温数据.作为一维综合孔径辐射计,FPIR 系统单次测量只能获取一个条带的亮温数据,通过载荷平台的移动进行推扫成像,以获取二维亮温图像.

图3 原始亮温分布
基于上述仿真系统,利用式(1)可仿真得到可见度函数. 在实际测量过程中,不可避免地存在测量噪声,所以利用均值为零方差为0.01×max(Vi)的高斯白噪声来模拟测量误差或者噪声. 然后,分别利用改进的最小范数正则化、改进的带限正则化和拉普拉斯混合正则化对含噪声的可见度函数进行重构,得到无混叠视场内重构结果,如图4 所示,其中图4(a)为纯海洋区域重构结果,图4(b)为海陆交界区域重构结果. 在图4 中使用的窗函数为汉宁窗,原始亮温分布也进行了加窗处理以便于比较. 从图4 中可以看出,与改进的最小范数正则化和带限正则化相比,拉普拉斯混合正则化重构误差明显降低,更加接近于真实亮温分布.
此外,计算了重构结果与原始图像之间的RMSE和PSNR. 表1 为图4 中纯海洋区域和海陆交界区域亮温分布经过不同成像算法后重构误差对比结果.

表1 不同成像算法的重构误差

图4 重构结果
为了进一步验证拉普拉斯混合正则化的鲁棒性,分析了噪声对重构结果的影响. 在式(1)可见度函数基础上加入不同方差的高斯白噪声,然后分别利用改进的最小范数正则化、改进的带限正则化和拉普拉斯混合正则化进行成像反演. 图5 所示为不同噪声情况下纯海洋区域重构结果性能. 在图5 中,当噪声为零时,改进的最小范数、改进的带限正则化和拉普拉斯混合正则化的RMSE 分别为0.05 K,0.06 K 和0.03 K. 从图5中可以看出,虽然测量噪声大小不同,但是拉普拉斯混合正则化比改进的最小范数和带限正则化重构结果RMSE 降低了40%以上,PSNR 提高了5 dB 以上. 值得注意的是,仿真中带限正则化的性能明显差于最小范数正则化,这是由于FPIR 样机天线单元数量仅有6 根,导致频率上覆盖的基线范围很小,从而导致带宽受限的约束性能不佳.

图5 不同噪声情况下纯海洋区域重构结果性能
类似地,不同噪声情况下海陆交界区域重构结果性能如图6 所示. 从图6 中可以看出,与改进的最小范数和带限正则化相比,在不同噪声情况下,拉普拉斯混合正则化重构结果RMSE 有效降低,PSNR 明显上升.此外,在图6中,当噪声为零时,改进的最小范数和带限正则化以及拉普拉斯混合正则化的RMSE 分别为1.46 K,1.64 K 和1.18 K. 对于海陆交界区域,由于观测亮温分布跨度大,其吉布斯振荡现象更加明显,残留的重构误差较大. 因此,对于海陆交界等亮温变化剧烈的场景,拉普拉斯混合正则化性能比改进的最小范数和带限正则化有一定的提升.

图6 不同噪声情况下海陆交界区域重构结果性能
综上所述,本文提出的拉普拉斯混合正则化方法对于测量误差或者噪声干扰具有良好的鲁棒性,对于不同的观测场景都能有效地降低其重构误差,尤其是对于纯海洋区域.
拉普拉斯混合正则化的计算时间与矩阵G的大小密切相关. 当矩阵G大小为31×91 时,在2.4 GHz Intel i5-4210U 处理器和12 GB 内存的笔记本电脑上,改进的最小范数正则化、改进的带限正则化和混合正则化的Matlab 计算时间分别为0.159 6 s,0.112 6 s 和0.318 3 s.结果表明,虽然拉普拉斯混合正则化能有效地提高反演的精度,但是需要花费更长的计算时间,其计算时间大约是改进的最小范数正则化的两倍. 对于大型的综合孔径天线阵列,可利用GPU 平台来计算拉普拉斯混合正则化反演结果以加快计算速度.
5 结论
高效的成像反演算法是综合孔径辐射计的关键技术之一. 综合孔径辐射计干涉输出的是可见度函数,成像反演算法的目的是将可见度函数重构为精确的辐射亮温图像. 然而,综合孔径辐射计成像反问题是病态的,虽然传统的正则化方法能有效克服其病态性,但依然存在较大的重构误差. 针对上述问题,提出了一种基于拉普拉斯算子的综合孔径辐射计成像算法. 该方法通过引入新的拉普拉斯算子项,对差分亮温构造拉普拉斯混合正则化,并利用多维扩展的广义交叉验证准则选取2 个正则化参数. 与传统的单一正则化相比,其优点在于通过添加2 个约束项来构造拉普拉斯混合正则化,以反映原始亮温分布的多尺度特征,从而得到更精确的反演亮温结果. 利用研制的L 波段FPIR 样机进行了仿真分析,仿真结果表明:与改进的最小范数正则化和带限正则化相比,本文方法重构结果更加接近真实亮温分布,能明显降低重构误差,并且具有良好的鲁棒性.
