车辆路径问题研究进展

蒋华伟，郭 陶，杨 震

（1. 粮食信息处理与控制教育部重点实验室(河南工业大学)，河南郑州 450001；2. 河南工业大学信息科学与工程学院，河南郑州 450001）

1 引言

近年来，由于国内外突发性公共事件和自然灾害时有发生，应急管理工作的顺利进行显得尤为重要，而车辆路径问题作为其核心问题，直接影响应急管理工作能否快速、高效地开展. 此外，随着物流运输业的迅猛发展，道路车辆和物流量急剧增长. 因此，为了高效开展应急管理工作，提高车辆配送效率，研究人员对车辆路径问题（Vehicle Routing Problem，VRP）进行了大量研究，并取得了显著的成果.

笔者分别在中国知网和Web of Science核心合集中以“车辆路径问题”和“Vehicle routing problem”为关键词，检索了近十年的期刊论文，并对每一年的论文数目进行统计，其结果如图1 所示. 从2010 年至2019 年，中国知网上有关车辆路径问题的期刊论文共3 634 篇，其中2013 发表在《系统工程理论与实践》上的一篇文章被引用152 次；Web of Science 核心合集上的发文量为4 799篇，其中高被引论文70篇，2013年发表在TOP期刊European Journal of Operational Research上的一篇文章被引用421次. 从近十年的发文量上来看，基本呈递增趋势，由此可以看出VRP仍然是目前学者研究的热点领域.

图1 VRP求解算法研究趋势

VRP 自1959 年 由Dantzig 和Ramser［1］首次提出之后，便受到许多专家学者的高度关注. 该问题指对具有不同物资需要的需求点，由配送中心对其进行物资配送，通过规划合理的行车路线，使得成本（如路程最短、耗费时间最少等）最小化，其示意图如图2 所示. 作为一种经典的组合优化问题，VRP 已被证明是NP-hard 问题［2］，即当问题规模很大时求解最优路径非常困难. 近年来，随着社会经济的发展，越来越多的VRP 变体问题被得以提出，逐渐成为研究的热点，如带时间窗的车辆路径问题（Vehicle Routing Problem With Time Windows）［3］、多配送中心车辆路径问题（Multi Distribution Center Vehicle Routing Problem）［4］、多目标优化的车辆路径问题（Vehicle Routing Problem Based on Multi Objec-tive Optimization）［5］、动态车辆路径问题（Dynamic Vehicle Routing Problem）［6，7］及大规模车辆路径问题（Large Scale Vehicle Routing Problem）等［8，9］.

图2 VRP场景示意图

根据VRP 求解方式的不同，目前VRP 的优化求解算法可分为精确算法、启发式算法和机器学习相关的算法三大类，图3给出了具体的VRP 求解算法分类. 其中，精确算法一定可以求出问题的最优解；启发式算法能在可接受的计算成本（计算时间、占用空间等）内，给出一个近似最优解；机器学习相关算法利用自动学习特征这一优点，可求得问题的近似最优解. 本文对这些算法的发展现状及存在的问题进行了总结分析，并对未来的研究趋势进行了讨论.

图3 VRP求解算法分类

2 精确算法

精确算法是针对某一具体问题建立相应的数学模型，然后利用数学方法进行求解，通常用于求解问题的最优解，常用的精确算法有分支定界法、列生成法和动态规划法等.

2.1 分支定界法

分支定界法（Branch And Bound，BAB）［10］由“分支”策略和“限界”策略两部分组成，采用广度优先或最小耗费优先的方法，在问题的解空间树上搜索可行解，并在找不到比当前解更好的解时修剪子树，是一种广义搜索穷举算法，其原理如图4所示.

图4 分支定界法求解原理

由图4 可知，采用分支定界法对VRP 进行求解时，把全部可行的解空间不断分割成越来越小的子集，通过设置子集的上界或下界判断子集是否需要进行下一步的划分，缩小解的搜索范围，减少计算量. 求解VRP 时，其目标一般为最小化成本，对于问题F（x），其松弛问题RF（x）的最优解即可作为问题F（x）的一个下界，将F（x）分解为两个新的子问题，其划分如式（1）所示.

由式（1）可知，分支定界算法执行的效率取决于问题解空间的上下界，寻找的上下界越紧凑，算法的执行效率越高. 由于需要对问题的所有可行解空间进行搜索，对于规模稍大的VRP 来说，其所有可行解空间无疑是庞大的，因此使用分支定界法对VRP 进行求解需要耗费很长的时间. 为此，Pecin 等［11］提出了分支价格和消减（Branch Price and Cut，BPC）法来求解带时间窗的VRP，当使用标记算法计算难以求解实例的列生成定价子问题时，使用弧子集代替节点子集，减少了计算复杂度，从而加快了算法求解VRP 最优解的速度. 另外，Ceselli 等［12］为求解废物管理系统中的VRP，通过在分支定界框架下动态生成行和列，对定价问题提出特定的精确算法，减少了寻找最优解的时间. 此外，针对分支定界法中搜索树存在的对称性问题，Santos 等［13］在求解两级容量受限VRP 时，设计了一个新的集合分区重构方式，使其不涉及按车辆索引的变量，消除了搜索树中存在的对称性问题.

2.2 列生成法

列生成法［14］是求解VRP 的一种高效算法，目前先进的求解VRP 的精确算法大多是基于列生成法形成的. 采用列生成法求解时，根据文献［14］将问题分解为限制主问题和定价子问题. 一般主问题为一个带有二元变量的划分问题，子问题为一个约束最短路径问题.将其应用于VRP 中，分解后的子问题和限制主问题分别如式（2）、式（3）所示［15］.

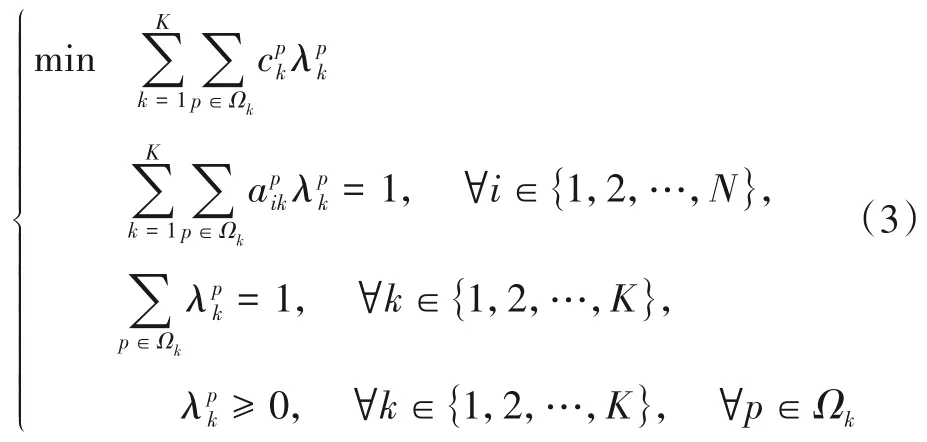
其中，K为车辆总数；Ck表示第k辆车的最大载重；N为节点总数；A表示节点之间弧的集合；S表示节点集合；Ωk表示车辆k的有效路径集合；d（i，j）表示节点i与j之间的距离；qi表示节点i的需求量；表示车辆k的行驶路线p的成本；表示在路径p下节点i被车辆k访问的次数；表示车辆k在路径p的极值点；ai和bi为节点i的时间要求.

由式（2）、式（3）可知，列生成法并不是同时处理所有的可行解，而是基于当前生成列的子集，通过限制主问题进行优化求解，当其余的可行解可以改善当前限制主问题的最优解时，才会进入该子集. 但由于列生成法只能求解线性松弛问题，在使用列生成法求解VRP时，一般将其与其他精确算法相结合. 为此，Hernandez等［16］在求解带时间窗的VRP 时，使用两组覆盖公式和分支定价法对问题进行求解，为减少计算量，使用列生成法计算其下界，在列生成过程中，对受限主问题和定价问题进行迭代求解，当定价问题无法为受限主问题找到新的潜在改进列时停止，有效降低了VRP 的求解时间. 此外，Pecin等［17］为求解容量受限的VRP，在分支削减和价格算法（Branch Cut and Price，BCP）中使用列生成法，将列与ng-路由关联，采用标签算法求解相应的定价子问题，同时当列生成法出现严重的收敛问题时，BCP 算法会自动执行双重稳定，防止算法在求解VRP 时过早收敛.Fukasawa 等［18］采用分支定价算法与列生成相结合的方式求解容量受限的VRP，首先使用分支定价算法求解根节点，并记录得到的下界和运行时间，再次求解时采用列生成法寻找其下界，以平衡下界的优劣与寻找更优下界所耗费时间之间的关系，提高算法的整体运算效率.

2.3 动态规划法

动态规划算法［19］求解时将复杂的原问题分解为相对简单的子问题，然后把子问题的解合并得出原问题的解. 采用动态规划法求解VRP，根据VRP 的优化目标，即总成本最小（总行驶距离最短、总运输成本最小或总服务时间最短），将其看作一个多阶段决策问题，分解成一系列的单阶段问题. 当每一个单阶段问题的成本最小时，该问题的总成本一定是最小的. 访问所有节点需要的成本可由式（4）表示［20］.

其中，β用于记录车辆运输期间的时间，初始值为相应操作的开始时间，当访问到车场时则重置为初始值；V=｛0，1，…，n｝表示节点集；Φ表示访问节点的集合，Φ∈V；表示从车场a1到节点j的时间相关成本，表 示从节点i到节点j的时间相关成本表示从节点j到车场a1的时间相关成本；(Φ，j)表示从车场a1开始访问Φ中所有节点一次且最后一个节点是j所需成本；*表示访问完所有节点并返回车场a1的最小总成本.

采用动态规划法求解VRP，在计算时可以利用实际知识和经验提高求解效率，但由于指数型内存和计算时间的要求，往往会产生维数灾难问题，其在大规模问题中的适用性受到限制，为此，Soysal 等［20］针对绿色时间相关的容量限制VRP，提出了基于加权随机抽样的约束动态规划方法，通过执行一系列的模拟递归来改进可行解，且每一次递归都可能选择不同的部分行程集合，该方法虽然不能保证找到问题的最优解，但是适用于处理大规模VRP 问题. 此外，Xiao 等［21］研究了具有时间依赖性的CO2排放优化VRP，提出了混合遗传算法和动态规划算法相结合的方法求解该问题，使用动态规划算法确定车辆在给定行车路线中的最优时刻表，借助算法的多项式级复杂度，减少了问题的计算时间，提高了求解VRP 的运算效率. 同时，Marinelli 等［22］为求解考虑环境因素的两级容量VRP，采用动态规划方法，利用FCM 聚类将主问题分解为若干个子问题，使用精确算法来获得每一个子问题的第一个解，并结合2-opt、Or-opt 和轮盘赌方法重新分配需求点，对得到的每个新的子问题应用精确算法求出其第二层的最优解，以此不断优化问题的可行解.

求解VRP 时，传统精确算法通常以时间和空间的复杂度为代价来换取解的质量，在求解时引入了严格的数学方法，其计算时间会随着问题规模的增大呈爆炸式增长，从而导致精确算法的性能大大降低，甚至无法求出最优解，因此只能将其应用于小规模VRP 求解中.

3 启发式算法

采用精确算法求解VRP 时，随着问题规模的逐渐增加，其时间复杂度快速增长，使得算法的求解性能不断降低，因此为高效求解大规模VRP，国内外学者将研究的重点转向采用启发式算法对VRP进行求解.

启发式算法是相对于最优化算法提出的，在可接受的范围内给出待解决组合优化问题的一个可行解，该可行解与最优解的偏离程度一般不能被预估. 相比于传统的精确算法，在处理大规模VRP 时，启发式算法具有更高的鲁棒性、可行性. 目前用于VRP 求解的启发式算法有很多，主要包括蚁群算法、遗传算法和其他算法（如智能水滴算法、粒子群算法和禁忌搜索算法等）.

3.1 蚁群算法

蚁群算法是由Dorigo 等［23］在1991 年提出的，由于蚂蚁根据信息素浓度选择路径，并在运动过程中释放信息素，因此某一路径上经过的蚂蚁越多，信息素浓度就越高，则后面的蚂蚁选择该路径的可能性就越大. 蚁群寻找最优路径的原理如图5所示.

图5 蚁群寻找最优路径原理图

路径（i，j）上t+n时刻信息素的更新由式（5）、式（6）和式（7）确定.

其中，τij（t+n）和τij（t）分别表示t+n和t时刻路径（i，j）上的信息素；ρ表示一个系数，（1-ρ）表示信息素挥发系数；△τij（t）表示路径（i，j）上的信息素增量；表示在时刻t和时刻t+n之间第k只蚂蚁在路径（i，j）上释放的信息素；Q为常数；Lk表示第k只蚂蚁走过的长度.

当使用蚁群算法求解VRP 进行信息素更新时，由于路径上的初始信息素匮乏，蚂蚁在选择路径时并不能充分利用已知信息. 为此，Kuo 等［24］为解决动态VRP，在模糊蚁群算法中引入一种聚类插入算法，以此获得更好的初始信息素，相比于使用随机初始信息素，提高了算法求得VRP 最优解的概率. 此外，Tang 等［25］在求解带软时间窗的多站点异构VRP 时，根据最近原则将问题分组后，使用扫描算法构造初始路径，同时引入遗传算子，自适应调整交叉概率和变异概率对模型进行求解，并采用平滑机制以提高蚁群算法求解VRP的性能. 当VRP 规模很大时，蚁群算法的收敛速度变慢且易陷入局部极值，针对这一问题，Zhang 等［26］为求解具有弹性时间窗的多目标VRP，在蚁群算法中引入变异算子对随机选取的解进行邻域搜索，并使用交换算子、移位算子和逆算子保持种群多样性，防止陷入局部最优. 此外，胡蓉等［27］在求解绿色VRP 时，采用动态信息素浓度挥发系数并加入系数控制因子，避免算法过早收敛，同时设计4种变邻域操作进行两阶段的局部搜索，以平衡全局和局部搜索并增强算法求解VRP 的能力. 另外，Mavrovouniotis 等［28］在蚁群算法中引入3种移民方案用于求解动态VRP，其中随机移民用于保持种群多样性，避免算法过早收敛，精英移民和记忆性移民用于维持迭代后期种群的多样性，从父代种群中获取优良个体，以提高算法的适应能力.

当处理多约束问题时，问题的复杂度会增加，例如在解决多配送中心车辆路径问题时，不仅需要考虑各需求点的配送顺序，而且要对需求点所属配送中心进行处理，难以在整体上对该问题进行优化. 为此，Narasimha 等［29］在求解最小-最大多配送中心VRP 时，证明了等面积的区域划分有利于求解问题的最优可行解，并采用卡尔松区域分割方法将区域划分为与配送中心数相等的分区，然后使用蚁群算法对每一分区的需求点进行路径寻优，最后将每一区域的最优解合并成整体最优解. 此外，Yao 等［30］针对多站点车辆路径问题，将其转化为一个带有虚拟站点的车辆路径问题，来降低问题复杂度，并采用扫描策略帮助蚁群算法跳出局部最优解，同时引入交叉运算来扩大算法的搜索空间.

3.2 遗传算法

遗传算法［31］是由生物进化思想启发得到的一种全局优化算法，包括选择、交叉和变异3 个算子. 使用遗传算法求解VRP 及其变体问题时，将其可行解编码成用一串数字表示的个体（染色体），然后通过选择、交叉和变异操作对种群中的所有个体进行更新优化，经过多次迭代得出最优解，式（8）表示如何选择个体进行交叉与变异，其求解过程如图6所示.

图6 遗传算法求解过程

其中，Pcross表示交叉概率；Pvariation表示变异概率；f1（X，Y）表示个体X与Y进行交叉；f2（i）表示个体Z的第i个位置发生变异.

由式（8）可知，采用遗传算法求解VRP 在进行交叉和变异时具有很大的随机性，且算法存在易早熟和收敛速度慢等缺点，因此为提高遗传算法求解VRP 的性能，研究人员对其开展了大量的工作. 为避免在求解时算法陷入局部极值，Sripriya 等［32］在求解带时间窗VRP时，采用分裂变异算子，将当前解暂时转移到一个更差的解来逃避局部最优解，只有当后代被双亲控制且路径的分裂发生在一个随机点上时，才会应用分类突变，从而避免陷入局部极值. 此外，Bouchra 等［33］为研究静态和动态2种情况下带软时间窗的VRP，提出了一种将遗传算法与变邻域搜索相结合的混合优化方法，采用遗传算法求得初始解，并使用2种邻域结构对初始解进行优化，第一种邻域结构在另一个随机选择的控制点之前，执行从排列中随机选择的控制点的插入，第二种邻域结构在距离当前可行解较远的区域内进行搜索，以避免陷入局部极值. 另外，Wang 等［34］针对随机需求下两级容量限制的VRP，采用路径复制交叉算子和基于卫星选择的变异算子，以最大限度地增加种群多样性，避免算法陷入局部极值. 由于遗传算法对初始种群的质量具有很大的依赖性，采用随机生成的方式进行种群初始化对最终解具有很大影响，为此，Ma 等［35］为求解具有时间窗和多决策者的VRP，将染色体上每一位置的值表示为对应需求点的优先级，其值越大则表示优先级越高，然后基于优先级的方法对种群进行初始化，以提高初始种群的质量. 此外，Erfan 等［36］在遗传算法中引入模拟退火算法，用于研究绿色容量限制VRP，利用模拟退火算法生成初始解，提高初始种群的质量，从而提高遗传算法求得更优解的概率.

当涉及大规模VRP 求解时，不仅计算成本高，其收敛速度也明显变慢，使得算法的性能显著降低. 因此，Wang 等［37］提出一种具有局部搜索的自适应遗传算法，用于求解多站点VRP，根据适应度值，采用自适应速率策略更新交叉和变异概率，并结合局部搜索以加快算法的收敛速度. Cattaruzza 等［38］为求解带时间窗的VRP，在遗传算法中引入局部搜索算法和分割算法，有选择地对某一个体进行局部搜索，加快收敛速度，从而提高遗传算法的性能.Pierre等［39］在研究带时间窗的多目标VRP 时，提出一种随机局部优化循环移位交叉算子，将其用于遗传算法中，并结合简单随机规则和顺序附加策略对问题进行求解，解决了传统遗传算法无法进行局部优化的问题，加快了收敛速度.

3.3 其它算法

除蚁群算法和遗传算法外，智能水滴算法、粒子群算法和禁忌搜索算法也常被用于求解VRP. 研究人员对上述算法加以改进，使其在求解VRP 时具有更好的性能.

智能水滴算法［40］是通过模拟自然界中河水与周围环境相互作用的过程所提出的一种新的基于随机群的群体智能计算方法，可用于解决组合优化问题，其中水滴速度和土壤值的更新如式（9）所示.

其中，velk（t+1）和velk（t）分别为t+1 和t时刻水滴k的速度；av，bv和cv表示水滴k中水流速度之间非线性关系的静态参数；soil（i，j）为局部路径中土壤量的倒数；soilk为水滴k携带的土壤量；ρn为一个非常小的正数；△soil（i，j）为从路径上移除时由水滴携带的土壤量；as，bs和cs表示△soil（i，j）和velk的逆之间非线性关系的静态参数；time（i，j：velk（t+1））表示水滴k从i到j的运动时间；HUD（i，j）表示位置i与j之间的启发式期望度.

由式（9）可知，水滴速度与水滴携带的土壤量相互作用，直接影响水滴搜索路径所需的时间. 将智能水滴算法应用于VRP 及其变体问题，由于水滴运动的随机性，其易陷入局部极值且收敛速度较慢. 为解决这一问题，提高解的质量，Ezugwu 等［41］在求解多站点VRP 时，将模拟退火算法与智能水滴算法相结合，利用模拟退火算法的局部搜索特性优化智能水滴算法的参数，改善水滴的运动特性，提高算法从当前解转移到邻域解的能力，扩大搜索空间，提高所求解的质量. 此外，Teymourian 等［42］为求解容量受限VRP，使用改进的智能水滴算法作为一种新的自然启发优化算法，并结合调整后的布谷鸟搜索算法、局部搜索混合算法和后优化混合算法，以控制搜索中种群的多样性，从而避免算法陷入局部极值.

粒子群算法［43］利用群体中个体对信息的共享，使粒子的运动在解空间中产生从无序到有序的演化过程，其中粒子在迭代中，通过个体极值和全局极值更新其自身的飞行速度和位置，如式（10）和式（11）所示.

其中，ω称为惯性权重；c1和c2为加速因子；t为当前的迭代次数；r1，r2为介于（0，1）之间的随机数；Pi为粒子i到目前为止搜索到的最优位置，即个体极值；Pg为粒子群目前搜索到的最优位置，即全局极值；分别表示第i个粒子在时刻t+1 和t时d维的速度；分别表示第i个粒子在时刻t+1 和t时d维的位置.

由式（10）和式（11）可知，粒子通过不断地向当前搜索到的最优值移动来寻找全局最优，与其他算法相比，易于实现且收敛速度较快，然而在实际搜索VRP 最优解的过程中，随着迭代次数的增加，粒子的多样性逐渐丢失，导致算法易陷入局部极值，难以求出问题的最优解. 为了解决这一问题，Mirhassani 等［44］利用两种粒子群优化算法来有效求解开放式VRP，分别采用gbest和nbest 两种不同大小的邻域对速度更新公式进行改进，其中gbest 粒子群算法中每个粒子的邻域为整个群体，社会信息则为整个群体找到的最佳位置，nbest粒子群算法为每个粒子定义了较小的邻域，社会信息则反映了粒子邻域内交换的信息. 此外，Alinaghian 等［45］在求解与时间相关的竞争VRP 时，提出了带随机拓扑的粒子群算法，其中每个粒子在种群中随机选择m个粒子作为邻域，而不是与所有粒子相关联，如果迭代后粒子的适应度值没有提高，则随机修改其邻域，以此加快其收敛速度.

禁忌搜索是一种全局性邻域搜索算法［46］，通过局部邻域搜索机制和相应的禁忌准则来避免迂回搜索，具有搜索速度快、局部“爬山”能力强等优点. 采用禁忌搜索算法求解VRP 时，由于其对初始解的优劣有很强的依赖性，较优的初始解可以显著提高最终解的质量.此外，禁忌搜索算法是从点到点进行搜索的，因此其全局搜索能力较弱，难以寻求VRP 的最优解. 为解决这一问题，李国明等［47］在求解随机VRP时，将禁忌搜索算法与最近邻算法相结合，并对禁忌搜索算法中禁忌长度等进行自适应调整，引入自适应惩罚系数，以提高禁忌搜索算法的寻优能力和算法的鲁棒性. 此外，Zhang等［48］提出了Tabu-ABC 算法，将禁忌搜索与人工蜂群算法相结合用于求解具有现实约束的VRP，该算法充分发挥了两种算法的优点，使用人工蜂群算法对种群进行初始化，从而获得质量较高的初始解，提高了禁忌搜索算法的性能.

4 基于机器学习的VRP研究现状

采用启发式算法求解VRP 时，虽然为解决算法易陷入局部极值和收敛速度慢这两大缺点开展了大量的工作，但其求解性能仍受到一定影响，使获得的可行解与问题最优解之间存在较大偏差，尤其是启发式算法的不确定性使得求出的解具有不可复制性. 因此，为提高VRP 解的质量和唯一性，研究人员将目光转向机器学习算法.

近年来，随着机器学习技术在管理运筹学和计算机科学等领域的快速发展和成功应用，越来越多的研究人员将其应用于求解VRP，并取得了较好的进展. 机器学习算法是一类从数据中自动分析获得规律，并利用规律对未知数据进行预测的方法，主要可以分为监督学习、无监督学习和强化学习三大类，其中无监督学习和强化学习已被应用于VRP的求解中.

4.1 无监督学习

无监督学习可以自动从样本中学习特征，而不需要输入样本的标记，其中人工神经网络是最常见的一种无监督学习算法［49］. 人工神经网络通过调整内部神经元之间相互连接的关系，达到处理信息的目的，并具有自学习和自适应的能力，其神经元示意图如图7 所示. 图7中a1，a2…an表示神经元；w1，w2…wn表示相应的权值；b为偏置项；SUM 为加权和；f表示激活函数；t为输出.

图7 神经元示意图

由于VRP 为NP-hard问题，采用启发式算法仅可以求得其近似最优解，且在VRP 中存在诸多不确定因素，如道路堵塞、需求量未知等，在求解时难以及时根据实际情况做出决策. 为此，Steinhaus等［50］采用改进的自组织映射方法对容量受限VRP 进行求解，通过加强偏差项和引入新的约束机制使得网络可以探索更多的可行解，并提高解的可行性. 此外，Yoshiike 等［51］提出了一种求解VRP 的自组织神经网络模型，在第一阶段利用最大神经元模型将需求点聚类为不同的区域即将VRP分解成TSP问题，在第二阶段采用弹性网络模型求解每个区域的TSP，得到问题的较优解. 另外，Sheng 等［52］采用指针神经网络求解VRP，根据实际分布情况，不断学习输入节点与输出解决方案之间的映射关系，增强算法模拟实际VRP 的能力，并在神经网络中引入全局注意机制，提高了收敛速度. 同时，Yu等［53］在求解在线车辆路径问题时，提出一种新的基于深度强化学习的神经网络组合优化策略，将在线车辆路径问题转化成车辆路线生成问题，接着使用结构图嵌入式指针网络进行迭代求解，并基于深度强化学习不需要大量标记数据这一优越性来训练模型参数.Wang 等［54］采用神经网络模型对VRP 进行求解，通过不断对模型进行训练和参数调整，获得一个对实际VRP 中不确定因素模拟良好的模型，经实验证明，该网络模型求得的解的质量优于现有的学习算法.

4.2 强化学习

强化学习［55］用于描述在智能体与环境的交互过程中，如何通过学习策略达到最大回报或实现特定目标，其相互作用如图8 所示. 在采用强化学习算法求解VRP 时，通过车辆与配送中心、需求点及其他约束条件之间的相互作用，不断学习它们之间的隐藏关系，以寻找最优的车辆路径.

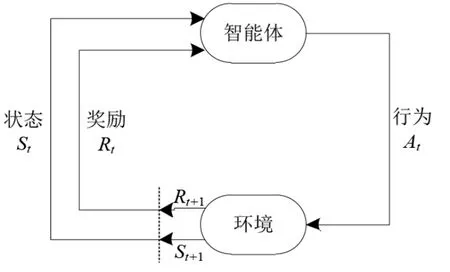
图8 智能体与环境的相互作用

图8表示智能体与环境的交互过程，即车辆路径与环境变化之间的交互，智能体通过感知环境的状态获得知识，并基于获得的知识选择要执行的动作，该动作作用于环境，环境根据其动作做出相应的奖励或惩罚，从而改变智能体的状态.

目前，研究人员侧重于求解各种约束条件下的VRP，但仅通过目标函数来简单地评价解的质量，然后基于当前解继续探索下一个可行解，并没有考虑将解的优劣程度进行数值化，以此用于下一个可行解的搜索. 为此，Peng 等［56］针对绿色VRP，提出一种基于强化学习奖惩机制的自适应局部搜索策略，来有效管理个体在多个邻域内的移动，并引导其进行搜索，相比于传统的局部搜索，基于强化学习机制的局部搜索能够有效地利用记忆功能管理邻域的移动，并引导其在最有希望的邻域内进行搜索，提高解质量的同时加快了搜索速度. 此外，Lopes 等［57］提出了一个采用元启发式进行优化的多智能体框架（Arquitetura Multiagente para Metaheuristica，AMAM），利用强化学习对带时间窗的VRP 进行求解，使智能体能够根据从与其他智能体及环境的交互中获得的经验来修改其行为，其中每个智能体在问题的搜索空间中独立行动，并通过环境来共享信息和进行协作，从而求得问题的近似最优解. 另外，Samma 等［58］将强化学习算法与粒子群算法相结合用于VRP 的求解，强化学习算法根据粒子的历史行为自适应地将粒子从一个操作转换到另一个操作，对表现良好的粒子给予奖励，对表现不佳的粒子进行惩罚，以此控制粒子的行为，使其向最优解的方向运动，加快了最优解的探索速度.Peng 等［59］提出一种具有动态编解码器结构的动态注意模型（Dynamic Attention Model，AM-D），该模型可以在不同构造步骤中动态地挖掘节点特征和隐藏的结构信息，在求解VRP 时，将其转化为马尔可夫决策过程，利用强化学习算法对AM-D 模型进行策略梯度训练.

5 算法分析

5.1 算法对比分析

近年来，国内外学者针对VRP 的求解算法展开了大量的研究，提出了许多高效的改进算法，但不同类型算法所适用的问题规模有所区别，为了后续更有效地开展相关领域的研究，本文在表1中给出了常用算法的优缺点及其适用场景.

表1 启发式算法及其优缺点比较

由表1 可知，采用精确算法求解VRP，虽然可以求出最优解，但当问题规模较大时，其求解速度会大幅度降低；基于启发式算法对VRP 进行求解，由于启发式算法在寻优过程中易陷入局部极值，且在迭代后期收敛速度变慢，使得算法难以获得问题的最优解，因而在使用启发式算法求解问题时，需要事先对算法进行改进，以提高算法的收敛速度或避免其陷入局部极值；机器学习相关算法在求解VRP 时，利用其可以自动从数据中学习特征这一优点，不需要事先人工干预，可自动进行路径寻优，挖掘数据的深度特征及数据之间的深层关系，但由于算法存在收敛速度慢且泛化能力差等缺点，还需对其进行进一步研究.

5.2 算法效果客观评价

为了客观地比较各种VRP 求解算法的性能与效果，本文选取分支定价法（Branch and Cut，BAC）、列生成法（Column Generation，CG）、蚁群算法（Ant Colony Algorithm，ACA）、禁忌搜索算法（Tabu Search，TS）、SOM神经网络和强化学习（Reinforcement Learning，RL）对带时间窗的多目标车辆路径问题（Multi Objective Vehicle Routing Problem with Time Windows，MOVRPTW）进行求解. 该问题的目标函数如式（12）所示.

其中，dist 表示个体X的总行驶距离；PW 表示所使用车辆数量的影响因子，是一个很大的常数；α用于衡量X中使用的总车辆数与可用车辆数之间的关系，若总车辆数超过可用车辆，则α为两者差的绝对值，反之则为α=k/K，k为所用车辆数，K为可用车辆数；β表示总服务时间的影响因子，0<β<1；P（t）为车辆延时访问的惩罚函数，其中t表示在个体X中车辆延时配送的总时长，表达式如式（13）所示.

实验数据集采用Solomon 标准测试集中的C102［67］，目前其已知最好解为828.94 km. 采用6 种算法对MOVRPTW 进行求解，计算对比结果如表2 和图9所示.

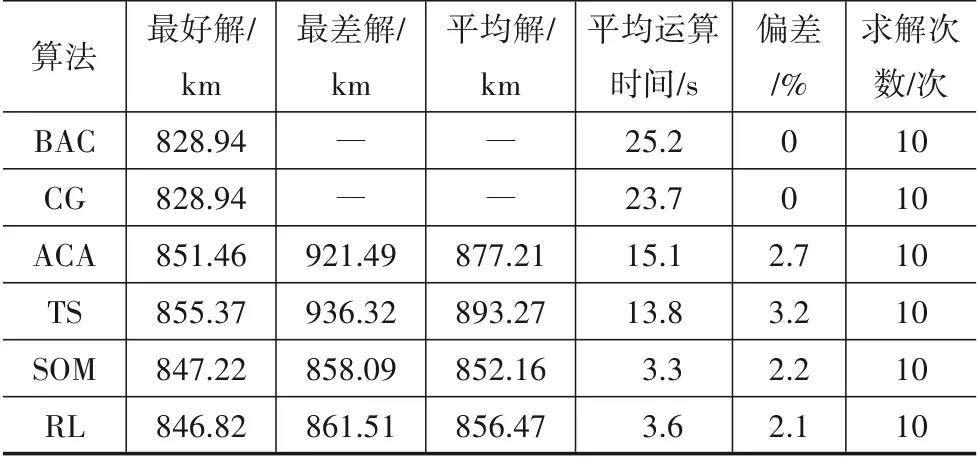
表2 六种算法所求解对比

由表2 可知，6 种算法在求解同等规模的MOVRPTW 问题时，精确算法BAC 和CG 可以求出问题的最优解，但其所耗费的时间远大于启发式算法和机器学习算法；机器学习算法SOM 和RL 与启发式算法ACA和TS相比，在求解时间上具有明显优势，且所求近似最优解与测试集目前已知最优解之间的偏差相对较小. 由表2 还可以看出，虽然启发式算法和机器学习算法在进行多次求解时所求出的近似最优解都不相同，但采用机器学习算法SOM 和RL 求得的解变化较小，与启发式算法ACA和TS相比机器学习算法稳定性更强.

从图9可以看出，随着迭代次数增加，6种算法的性能均有所提高. 相比启发式算法和机器学习算法，精确算法BAC 和CG 所求得的最优解较为稳定，这是因为精确算法针对MOVRPTW 问题采用具体的数学方法进行求解，稳定性较强.ACA 和TS 算法随着迭代次数增加，所求近似最优解的质量逐渐提高，在迭代20 次和迭代25 次之间，求得的近似最优解的适应度值有较大的波动，这是由于MOVRPTW 问题属于离散问题且采用的适应度函数包括路径距离、所用车辆数和总延迟时间3个因素，在进行25 次迭代时，算法搜索到更优的可行解，其距离、所用车辆或者延迟时间明显减少，使得可行解的适应度值产生较大的跳跃.SOM 和RL 算法求得的近似最优解的适应度值随着迭代次数的增加而提高，并逐渐趋于稳定，这是因为机器学习算法可以从数据中自动学习特征，随着迭代次数的增加，算法可以充分学习到数据之间的关系，提高可行解的适应度值.

图9 6种算法随迭代次数变化的趋势

综上所述，精确算法、启发式算法和机器学习算法在求解VRP 时，3 种算法自身的特点决定了所求得的VRP 解的优劣，且根据算法的性能，所适用的VRP 规模也不相同. 其中精确算法主要用于求解小规模VRP，且可以求得问题的最优解；启发式算法适用于求解大规模VRP，但只能求得问题的近似最优解，且解的优劣与算法的性能有关；机器学习相关的算法可以用于求解大规模动态VRP，其直接从数据中学习特征，挖掘数据之间的内在关系，从而求得问题的近似最优解，并且所求解的优劣与模型训练的好坏有关.

6 总结和展望

近年来，随着物流业的蓬勃发展及突发性公共事件和自然灾害的时有发生，VRP 作为物流业和应急管理工作中的关键环节，依然是研究人员高度关注的热点领域. 鉴于问题的复杂性和多变性，以及对当前算法求解有效性和准确性要求的不断提高，本文在总结近年来国内外学者对VRP 及其变体问题研究算法的基础上，尝试给出如下可能的发展趋势探讨.

（1）平衡启发式算法易陷入局部极值和收敛速度慢之间的关系

采用启发式算法求解VRP 及其变体问题时，往往面临着易陷入局部极值和收敛速度慢这两大缺点. 目前已有的工作在处理其易陷入局部极值这一问题时，无论是扩大其搜索空间还是采用自适应因子对算法进行调控，其本质主要是基于“变异”思想，以期望算法可以跳出局部极值. 这一方法可以在一定程度上避免算法陷入局部最优，但往往会增加算法的复杂度，并且随着个体“变异”次数的增多，算法收敛速度变慢. 因此，如何平衡算法易陷入局部极值和收敛速度慢之间的关系，仍是需要重点关注的问题.

（2）寻找新的“全局函数”对个体进行评价

使用启发式算法求解问题，一般仅通过适应度函数对个体的优劣进行评价，并且在更新种群时趋向于选择适应度值大的个体，然而这种方法易使算法在迭代后期因为种群多样性的缺失而陷入局部极值. 同时，笔者认为由于该优化问题属于离散问题，因此较优的父代个体并不一定能产生更优的子代个体. 因此，为了更好地评估个体的优劣并保留种群的多样性，可考虑引入一个有别于适应度函数的全局函数，该全局函数不仅考虑当前个体的优劣，同时考虑其父代个体的优劣，并赋予不同的权值，用于评价迭代中产生的每个个体，并根据该全局函数对个体进行选择和淘汰，以保证种群的多样性.

（3）加强动态车辆路径问题的研究

尽管VRP 已被提出很多年，但不同约束条件和不同目标的VRP 变体问题随着社会的发展和人们需求的变化逐渐成为研究的热点，其中动态车辆路径问题更是受到国内外学者的高度关注. 在实际的交通运输中，常遇到道路堵塞或者需求点物资需求不确定等情况，其由于具有很大的实时性和不可预测性，因此为车辆路径的优化带来了很大的挑战. 目前对动态车辆路径问题的研究主要考虑单一的动态因素，而在实际应用中，引起不确定的因素多种多样且可能存在相互影响，因此还需进一步加强对动态车辆路径问题的研究，尽可能多地考虑不确定因素与其之间的相互关系.

（4）深入开展机器学习相关的求解算法

由于精确算法仅适用于求解小规模VRP，而启发式算法存在易陷入局部极值这一缺点，这使得所求解的优劣与算法性能好坏密切相关，因此一种更加高效、稳定的求解方法有待提出. 鉴于机器学习的优越性，笔者认为有必要深入开展机器学习算法在VRP 中的应用研究，借助机器学习可以从数据中自动提取特征这一特点，在不同约束条件下，根据外界环境变化，自动学习配送中心、需求点与车辆之间的相关关系，以寻求它们之间的最佳匹配关系即最优路径，并经过多次训练之后，获得高效、准确的路径优化模型.

综上所述，研究和探索高效、精确的VRP 求解算法是目前需要解决的首要问题；如何平衡启发式算法易陷入局部极值和收敛速度之间的关系以及寻找新的“全局函数”对其个体进行评价是今后的主要发展方向；此外，还应将VRP 与实际交通运输紧密结合，加强对动态车辆路径问题的研究；同时，鉴于机器学习算法的优越性，未来在求解VRP 时需要对机器学习相关算法进行进一步的探索.