考虑参数不确定性的框剪结构敏感性分析*
2022-04-18杨鑫王惠民姚激黄坤龚云峰
杨鑫 王惠民 姚激 黄坤 龚云峰
(昆明理工大学建筑工程学院 昆明 650500)
0 引言
结构抗震领域存在诸多不确定参数,如结构固有阻尼、建筑物所用材料特性以及地震动随机性等,这些不确定参数将会影响到建筑结构的地震反应,使得地震需求呈现出不确定性,明确各不确定参数对地震需求影响程度的大小很有必要。敏感性分析的任务就是从选定的不确定参数中筛选出对地震需求影响较为显著的因素。依据敏感性结果可忽略非敏感因素,从而简化计算,极大提高分析效率。
张望喜等[1]以框架结构为研究对象,分析了推覆顶点位移对含加载方式在内的共9种不确定性参数的敏感性;尹犟等[2]对8度设防的典型框架结构进行敏感性分析,得出了随机参数的Tornado图形敏感性排序;蒋亦庞等[3]以无筋砌体结构为研究对象,采用IDA(增量动力法)和FOSM(一次二阶矩法)分析了不确定性参数与地震易损性两者间的关系。
以上关于不确定性参数对地震需求影响的研究对象大多局限于框架结构。而框剪结构作为高层、超高层常用的结构形式,也被广泛地应用于我们的民用建筑中,当发生地震时,剪力墙可以承担大部分输入的地震能量,给生命安全带来保障[4]。为此,我们着重探讨框架-剪力墙结构,采用Tornado图形法和数理统计方法考虑了结构地震需求对地震动、结构质量、材料特性、阻尼以及阻尼器参数(仅在有控结构中考虑)等在内的共8个不确定性参数的敏感性,并给出了相应的一些建议。
1 敏感性分析方法
Tornado图形由且仅由若干条平行的横杠组成,每条横杠也仅代表了1个不确定参数,横杠数量代表了不确定性参数的个数,而横杠“摆幅”宽度直观体现了不确定参数对地震需求量的影响程度。若某个参数影响显著,则其对应的横杠“摆幅”较宽,反之较窄。Tornado图形法具体步骤如下:
(1)确定地震需求参数(EDP)的类型,如结构基底剪力需求、层位移角需求等。
(2)任选一个不确定参数σ为变量,判断σ所属的分布类型,通过概率分布的上、下限(一般对应10%和90%)确定与之相应的变量下限值σLB和上限值σUB。
(3)明确所有考虑到的不确定性参数均值,每取一个不确定参数σ,就将除该参数外的变量固定为其均值,将σLB和σUB的数值代入模型运行时程分析,时程分析的结果即为需求上下限值RUB和RLB。
(4)取|RUB-RLB|为不确定参数σ对应的摆幅宽度,并表示在初始图形中,然后重复上述步骤直至获得所有不确定参数对应的摆幅宽度,将宽度按降序从上到下重组,重组后的图形称为Tornado图,图中摆幅宽度直观体现了EDP对输入变量的敏感程度。
对于一些特殊的不确定性参数,如地震动特征(除地震动强度外的其他特征),很难对其用概率密度函数进行描述,本文将通过数理统计方法研究EDP对所选不确定性参数的敏感程度。
2 结构模型
本文以高层框剪结构为研究对象,对结构中的随机参数进行敏感性分析。结构设计采用YJK软件,将设计好的模型通过其模型转化接口导入到SAP2000中,分别建立无控结构模型和带阻尼器的有控结构模型。结构参数具体如下:建筑总高度53.7 m,共13层,其中底层和11层层高为4.2 m,4层和12层层高为5.1 m,余下层高都为3.9 m。梁、柱混凝土强度为C35;梁、柱纵筋和箍筋等级为HRB400,构件配筋采用YJK计算结果,将其导入到分析模型中。建筑物位于8度(0.2g),Ⅱ类场地。其中有控结构采用墙式粘滞阻尼器,共88个,有限元模型见图1。
有限元模型中的楼板采用刚性楼板假定[5];阻尼单元采用连接属性的Damper-Exponential类型;在SAP2000中,分层壳基于复合材料原理,将壳单元法分成若干层,通过给定不同的材料和厚度来实现不同行为,这便于我们模拟剪力墙的非线性行为。该结构模型的剪力墙用5层壳进行模拟,即1层混凝土、1层横向钢筋和1层纵向钢筋,如图2所示,图中仅列出一侧钢筋。

图1 算例有限元模型

图2 剪力墙模拟示意
3 结构不确定性参数
3.1 地震动强度
依据文献[6]的研究结果,本文选取极值Ⅱ型作为地震动强度的概率分布,其概率分布函数表示如下:
PF(f)=exp[(-f/fe)-c]
(1)
式中,fe为众值烈度对应的地面加速度值,c为形状系数。
(2)
(3)
(4)
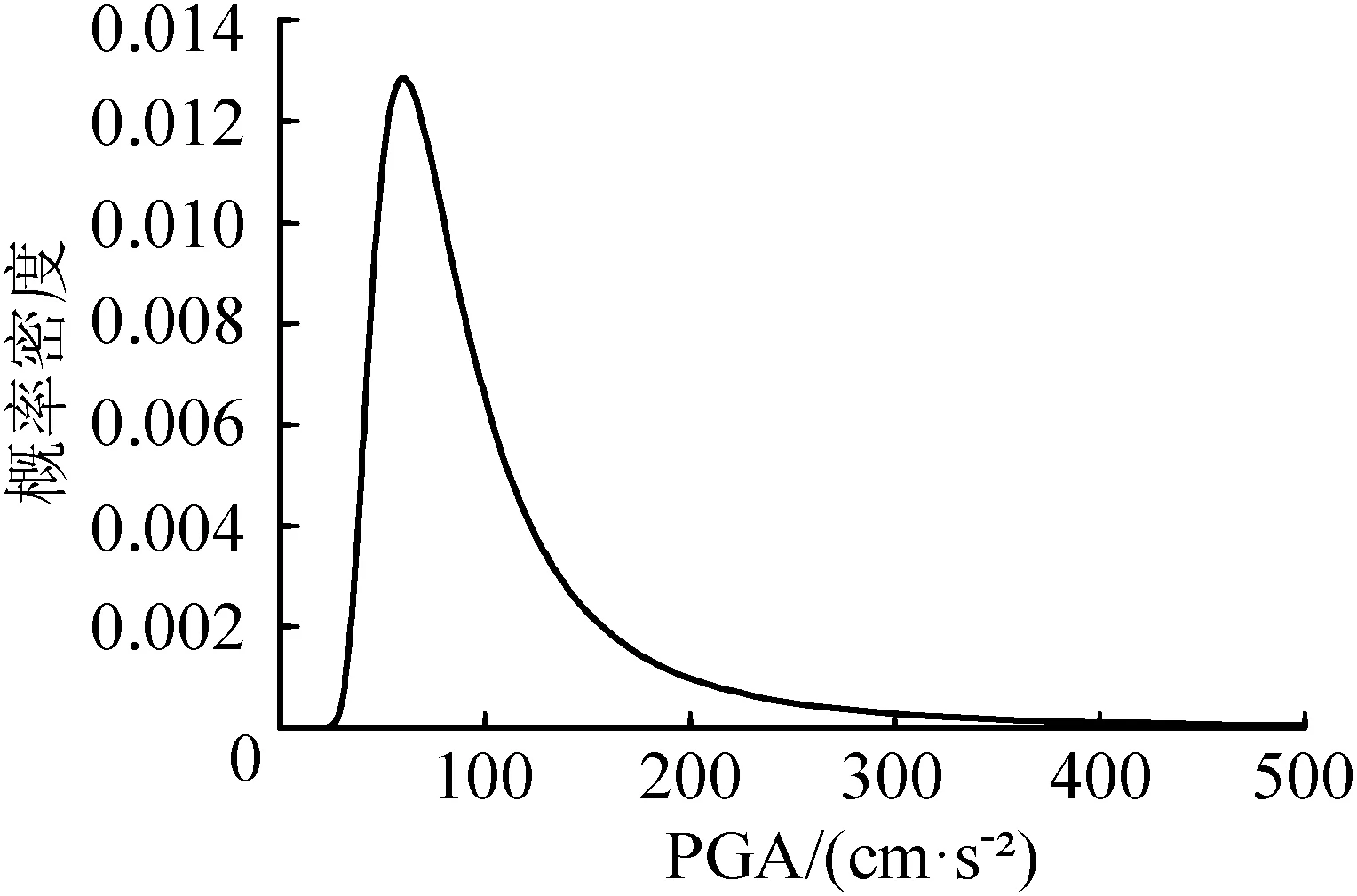
图3 地震动强度概率密度函数

图4 地震动强度概率分布函数
3.2 地震动特征
由于地震动特征没有明确的概率分布函数,本文采用HYUNG T L[7]介绍的方法确定该不确定性参数的均值及其上下限:
(1)从地震波库中选取一定数量且符合建筑物所处地场特征的地震记录。
(2)将所有结构特性的不确定参数及地震动强度设为其均值。输入上个步骤选好的地震记录进行时程分析,统计地震需求参数。
(3)依据统计结果绘制频数直方图,通过曲线拟合直方图,所得的曲线可近似看作该参数的经验概率密度函数。
(4)对上一步骤得到的概率密度函数积分,确定其均值和上下限;则与之相应的地震记录具有地震动特征的上限、均值和下限。
文献[8]指出,为了研究地震动的离散型,须选取20条及以上地震波。本文依据这一结论,选取了与该结构所处场地特征周期近似的20条地震强震记录进行时程分析,限于篇幅,仅列举了无控结构下地震动强度对结构基底剪力需求的结果。图5为结构基底剪力经验概率密度函数及公式拟合对应的均值和上下限;由图5可以看出拟合效果都很相似。

图5 基底剪力经验概率密度函数
3.3 结构材料和其他随机参数
依据前人的研究结果知,混凝土和钢筋的弹模可用概率密度函数描述,采用式(5)计算:
(5)
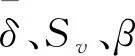
为方便输入有限元模型,将本研究考虑的不确定性参数及概率分布进行整理汇总于表1。

表1 不确定性参数分布
4 敏感性结果分析
图6为结构模型在未增设粘滞阻尼器情况下,结构基底剪力、顶点位移和最大层间位移角共3个地震需求参数对地震动强度PGA、地震动特征PGE、混凝土弹模ConE、钢筋弹模SteE、结构质量Ms、阻尼比Da的Tornado图形法敏感性结果;与图6不同,图7为结构模型在增设粘滞阻尼器情况下的Tornado图形法敏感性结果。各图中垂线表示所有不确定性参数取均值时的地震需求参数值。
由Tornado图形法特性知,横杠的摆幅体现了地震需求参数对不确定性参数的敏感程度。从图6可以看出,对于无控结构,无论是结构基底剪力需求、结构顶点位移或是最大层间位移角需求,影响显著的不确定性参数从大到小依次是地震动强度、地震动特征、阻尼比、结构质量、混凝土弹模和钢筋弹模。由图7可知,对于有控结构,就上述提及的3个地震需求参数而言,受地震动强度和地震动特征的影响依旧最为敏感;粘滞阻尼器的指数C和系数α影响程度次之;相比之下,结构质量、阻尼比、混凝土弹模和钢筋弹模的敏感性程度较低,且排列顺序也随地震参数需求不同而有所变化,在图6和图7中,钢筋弹模对应的摆幅最低,表明该参数对地震需求参数影响最小,因此在以后的敏感性分析中,采取忽略钢筋弹模不确定性的做法,既能大大简化分析的复杂程度,也能确保分析结果的准确性。

图6 无控结构Tornado图形法敏感性结果
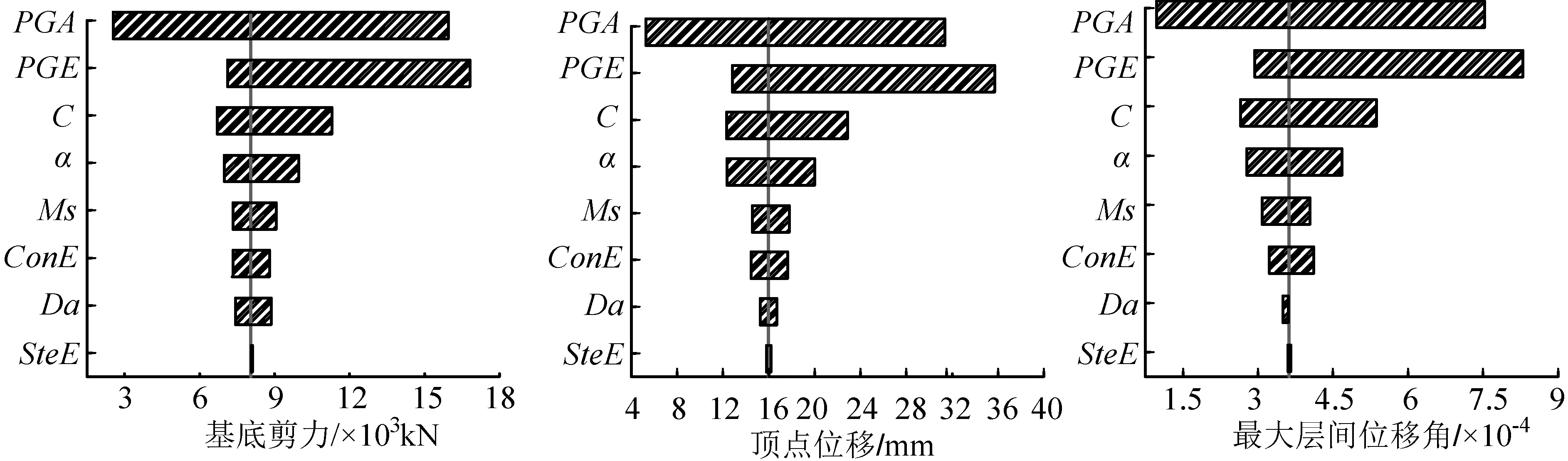
图7 有控结构Tornado图形法敏感性结果
5 结论
(1)对研究中选用的3个地震需求参数来说,无控结构受不确定性参数影响大小的排序为:地震动强度、地震动特征、结构阻尼比、结构质量、混凝土弹模和钢筋弹模。
(2)有控结构地震需求参数的不确定性参数受地震动强度和地震动特征影响较显著,其次为粘滞阻尼器的参数。除上述因素外,地震需求参数受结构质量、阻尼比和混凝土弹模的影响也较大,而钢筋弹模影响最小。
(3)增设粘滞阻尼器后,不确定性因素对应的摆幅均有所减少,合理选取阻尼指数C和阻尼系数α可以有效降低结构基底剪力、结构位移及位移角。
