多视角生成微专题 促进学生深度学习

卢秋丹

(闽清县第一中学，福建 闽清 350800)

微专题教学是指将某一知识点作为研究主题，从该知识的概念与原理出发，通过一条清晰的主线将零散的知识自然地串联起来，循序渐进地解决问题的一种“小切口”教学方法.“微”即细致入微，内容精而少；“专”即所选题目应根据相同的教学目标，集中解决同一类型的问题.高三数学二轮复习阶段，随着全国各地模拟试题的不断出炉，教师常常以习题讲评的形式实施复习教学.但由于数学知识跨度大，学生思维跳跃性强，在复习过程中易出现“高原反应”，复习效果不理想.

因此，教师应结合学生考试和练习中暴露出的问题，有计划、有目的地在二轮复习备考中采用针对性强、新颖灵活的“微专题”教学形式，从多视角切入与生成.这样有利于帮助学生构建完备的知识体系和数学研究的一般方法，促进思维的深层参与，实现深度学习，全面提升数学核心素养.

1 聚集“疑点”，生成“微专题”

对于教材中的“疑点”，教师虽然反复讲解，但收效甚微，学生遇到类似问题仍无所适从，究其原因，是教师“碎片化”的、“就题论题”的讲解无法给学生留下深刻的印象[1].因此教师应以突破学生的“疑点”为目标，选择学生作业和试卷中的一些“易混易错”问题，进行重组、加工，组织微专题主线教学，通过对此类问题的剖析，引导其透过现象反思问题的本质，掌握解决问题的思想方法，使复习收到事半功倍之效.

案例1以“基本不等式”的应用设计“微专题”.

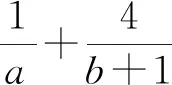
这是笔者所在学校高三单元测试中的一道试题，错误率较高.主要原因是学生对运用“基本不等式”求最值问题认知不足,当条件(一正、二定、三等)失效时，不能快速找准解题的“突破口”，且易忽视“等号成立”的条件.为此，教师以“基本不等式”最值问题构建以下微专题.

环节1温故热身.

问题2设正实数a,b满足ab=a+b+3，则a+b的最小值是______.

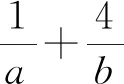
环节2拾级而上.

变式1已知正数a,b满足ab=a+2b，求a+b的最小值.

分析(变换题设形式)由ab=a+2b，得

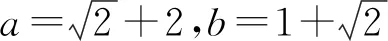
变式2设正数a,b满足ab=2a+b+3，求a+b的最小值.

分析由ab=2a+b+3，得

(a-1)(b-2)=5，

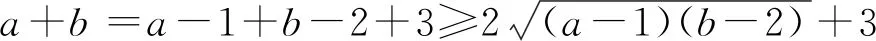
以下略.

评注此类问题的核心在于怎样通过“凑”达到基本不等式中“定”的条件,从“和定”转化为“积定”.

环节3渐入佳境.

问题4设a>0,b>0，a+b=1，则

( )

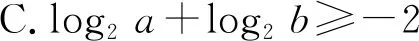
(2020年全国数学新高考卷Ⅰ第11题)

问题5设5x2y2+y4=1(其中x,y∈R)，则x2+y2的最小值是______．

(2020年江苏省数学高考试题第12题)

环节4引申拓展.

问题6设正数a,b满足4a2+b2=1，则2a+b的取值范围是______.

思路14a2+b2=(2a+b)2-4ab，然后运用“基本不等式”解决.

思路2设2a+b=t，则b=t-2a，代入已知转化为关于b的一元二次方程，根据判别式Δ≥0，求出范围.

评注通过“微专题”复习，有效提升了学生对此类问题的处理能力，提升了学生运用转化与化归等思想方法的能力.对典型问题进行一题多变，有利于学生突破教材的禁锢，引领学生由“变”的现象中揭示“不变”的规律，由“不变”的本质中寻找“变”的规律，从不同的背景中掌握通性通法发现问题的本质，从而厘清了知识与方法间的联系，提高复习的针对性、有效性，提升了学生的思维深度，发展了逻辑推理、数学抽象等核心素养.

2 围绕“高频点”，生成“微专题”

高考“高频点”是高中数学的核心知识，是考查数学核心素养的重要载体.因此教师应围绕“高频点”生成微专题，引导学生回归教材,梳理微专题中所涉及的知识与方法，并通过对数学问题的挖掘，抓住其精髓,深度领悟数学问题背后深层次的数学思想方法，进而形成对此类问题更为全面、深刻的认识，从而“润物细无声”地将数学学科核心素养融入其中.综观近几年的高考试题,不难发现“圆锥曲线离心率范围问题”是命题的高频点，教师可聚焦此类“高频点”，围绕回归教材、变式训练、链接高考、深化思维等设置微专题，引导学生探寻破题思路，提升解题能力，发展数学核心素养.

案例2以“圆锥曲线离心率范围问题”切入的“微专题”.

此类问题往往灵活多变，条件隐蔽，综合性强，是近几年高考的“高频点”，需要学生借助图形的几何特征对题目进行分析,从而找到问题解决的“钥匙”，提升学生的数学核心素养.

环节1回归教材，反思感悟.

问题1如何计算圆锥曲线的离心率？

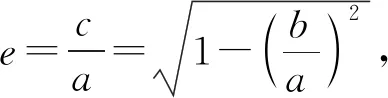
问题2求解圆锥曲线离心率范围问题的关键是什么？

探究a,b,c之间的不等关系.

问题3从哪几个方面寻求a,b,c之间的不等关系？

从已知出发；从椭圆与双曲线自身的性质出发；从圆锥曲线的几何特征出发.

环节2变式训练，由特殊到一般.

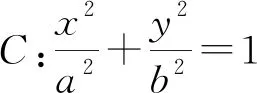
思路1运用三角形三边的关系确立不等式.

思路2运用焦半径性质确立不等关系.

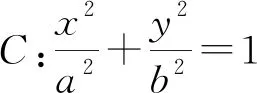
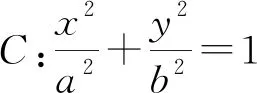
环节3链接高考，深化思维.

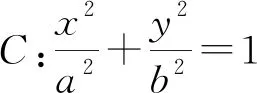
(2018年全国数学高考卷Ⅱ理科试题第12题改编)

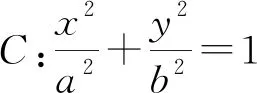
(2021年全国数学高考乙卷理科试题第12题改编)

评注学生的关键能力是在掌握“四基”的基础上，经过迁移，并进一步概括化、系统化而获得提升的[2].“圆锥曲线离心率范围问题”微专题承载着激活知识梳理、完备学生知识体系、培育其数学核心素养的功效.因此教师应从学生原有的认知基础出发，贴近其最近发展区设置微专题，精心设计问题串，构建解决某一类问题的“路线图”，引导学生在新情境的问题解决过程中获得数学体验，掌握研究问题的一般数学方法，使解决问题的能力达到一个新的高度.

3 挖掘教材“生长点”，生成微专题

编拟微专题不能只局限于知识的归纳整理，更要用数学思想方法引领微专题教学.课堂教学是预设与生成的和谐融合，高三复习教学也是如此.因此在“微专题”复习的设置与教学过程中，应考虑学生思维的多向性、过程的开放性等特点，引导学生深度参与，不断探询再生性知识的“生长点”.通过教师睿智的追问与引导，激发学生的思维，促进其更深度地思考问题，并生成深层次的认知，使学生的思维实现质的飞跃.

案例3一道教材习题切入的“微专题”.

环节1课本溯源.

问题1已知圆x2+y2-6x+5=0,过原点的直线与该圆交于点A,B，求弦AB中点M的轨迹方程.

(人教A版高中《数学(选修2-1)》第37页A组习题第4题)

评注问题1起点低，有多种解决问题的思路，教师引导学生多方位、多角度进行探究.

思路1(直接法)如图1，设圆x2+y2-6x+5=0的圆心为C，则点C的坐标为(3,0).

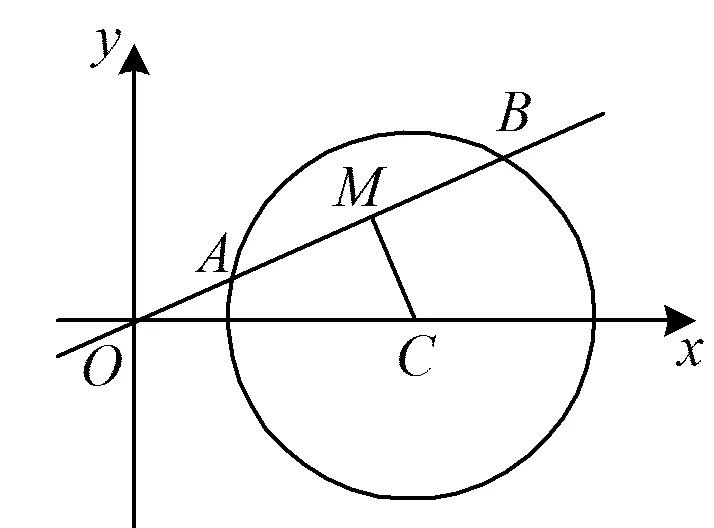
图1

设M(x,y)，若直线AB与x轴不重合，由CM⊥AB,得

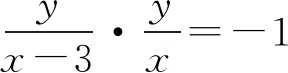
整理得

x2+y2-3x=0(其中x≠3,x≠0).

若直线AB与x轴重合，则M与圆心C重合，满足题意.

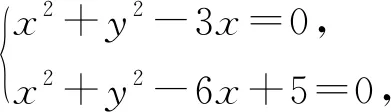
因此所求轨迹的方程为

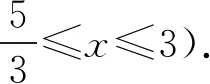
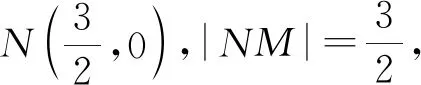
思路3(几何法)若直线AB与x轴不重合，无论弦AB怎样变化，由△OCM为直角三角形，可得

|OM|2+|CM|2=|OC|2,

即

x2+y2+(x-3)2+y2=9，

即

x2+y2-3x=0(其中x≠3,x≠0).

下同思路1.

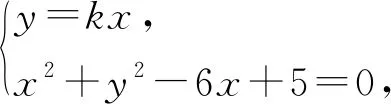
(1+k2)x2-6x+5=0，

则

当k≠0时，消去k，得

x2+y2-3x=0.

当k=0时，M(3,0),满足上式.

由Δ=16-20k2≥0，得

从而

故点M的轨迹方程为

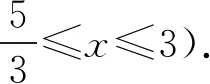
环节2由特殊到一般.

问题2过点P(m,n)的直线和⊙C:(x-a)2+(y-b)2=r2交于点A,B，求弦AB中点的轨迹方程.

性质1已知⊙C:(x-a)2+(y-b)2=r2，过点P(m,n)的直线与C交于点A,B，设M为弦AB的中点，那么当点P在⊙C外时，点M的轨迹是⊙C1在⊙C内之部分；当点P在⊙C内(点P与点C不重合)时，点M的轨迹是⊙C1,其中⊙C1的方程为

环节3引申推广.

问题3若问题2推广到椭圆、双曲线和抛物线，则点M的轨迹如何？

学生参与的积极性很高，经过探究，得到如下性质：

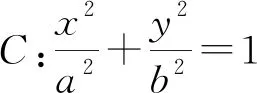
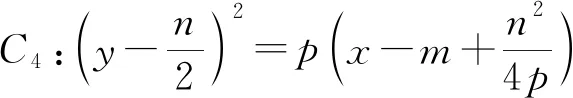
性质5经过一定点的直线与圆锥曲线相交，这条弦中点的轨迹是与原曲线类型相同、形状相似的曲线(其曲线是原曲线内的部分)

评注从一道平淡的课本习题出发，引导学生积极参与、主动探究，由特殊到一般，深挖题目的“生长点”，并进行引申推广，以小见大.在解决问题的过程中，学生品尝到了成功的愉悦，催生了深度学习的智慧，培养了发现问题、探究问题的能力，使学习过程成为提升核心素养的丰富载体[3].

总之，教师应基于微专题“切口小、定位准、形式多”等特点，选择经典问题，及时弥补学生所暴露出的问题.同时，教师在设计微专题时，应重视数学知识与思想方法的整合、串联，由易到难，由表及里、循序渐进地引导学生深度参与，经历回归基础、逻辑推理、抽象概括等活动过程，使学生由“见山是山”的浅层学习达到“见山不是山”，再上升到“见山还是山”的深层境界，从而让数学核心素养在高三复习教学中真正落地生根.