溯错误之源 探解题之径 开素养之门——一道质检题的探究与思考

刘 坭

(上海市第五十二中学，上海 200083)

在教学中，笔者发现在解决立体几何问题时，许多学生过于依赖空间向量，热衷于所谓的“通性通法”，而忽视直观感知、操作确认的环节，这给立体几何的学习埋下了隐患.在立体几何的复习备考过程中，遇到这样一道题：

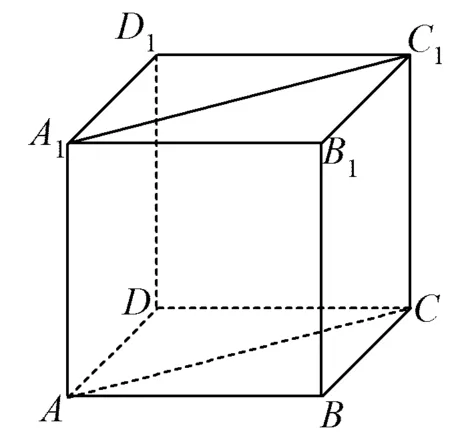
图1

生1:建立如图2所示的空间直角坐标系，因为点P是平面ACC1A1上一动点，可设点P(x,2-x,z)，而点D1(0,0,2)，C(0,2,0)，所以

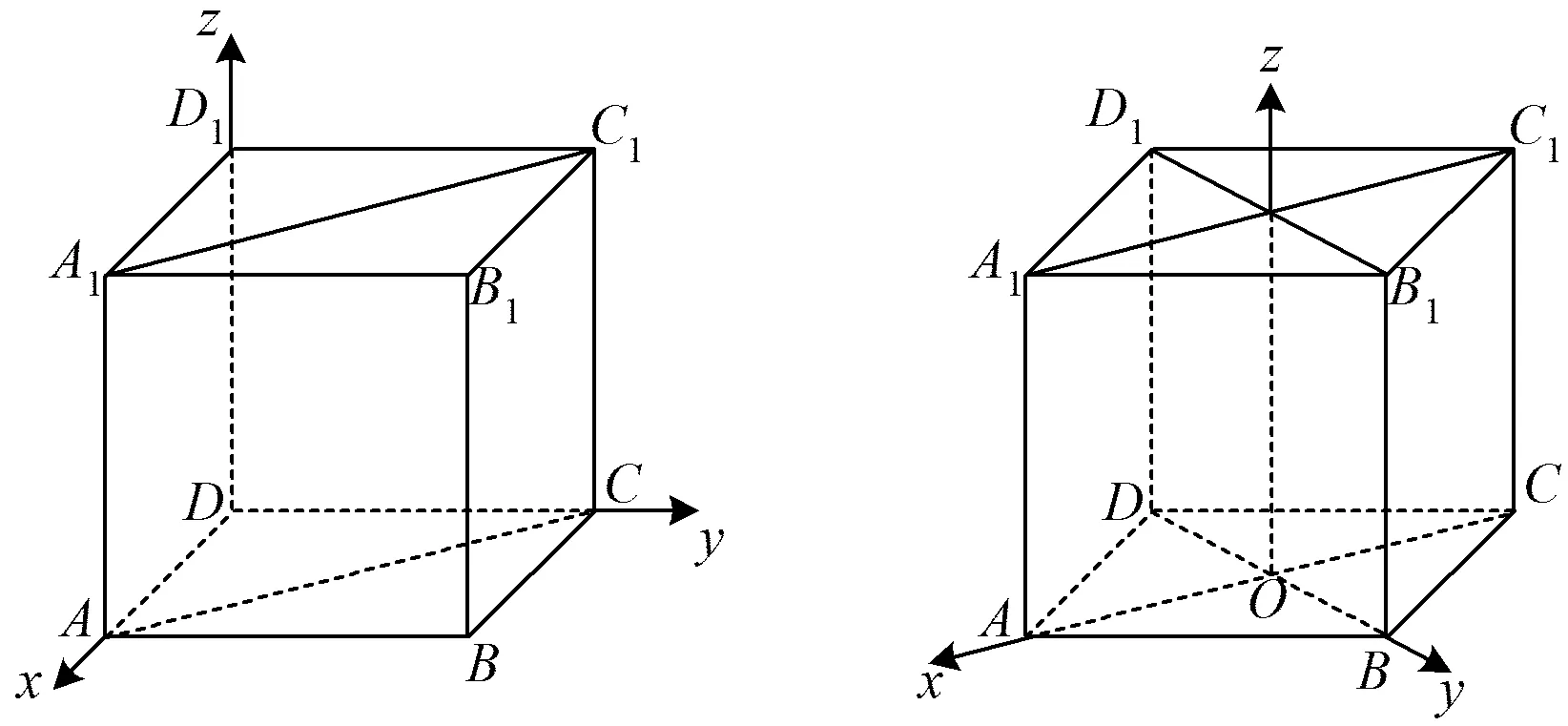
图2 图3

2x2-2x+z2-2z=0，

即

故点P所围成的平面区域是椭圆.但椭圆的面积无从求得.

生2在生1的基础上加以补充，给出了解法1.

即

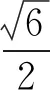
1 深度学习，释疑解惑

我们知道，在平面直角坐标系中点与有序实数对(x,y)是“一一对应”的，因此二元方程F(x,y)=0表示平面几何图形，比如圆、椭圆、双曲线的方程.而在空间直角坐标系下，如果适合方程F(x,y,z)=0的点的集合是某个曲面∑，那么就把曲面∑称为该方程的图形，而把该方程称为曲面∑的方程[1].简而言之，三元方程F(x,y,z)=0表示曲面.

x2+y2-2y+z2-2z=0,

即x2+(y-1)2+(z-1)2=2,

(1)

x+y=2,

(2)

点P的坐标同时满足式(1)和式(2)，联立方程得

(3)

将方程组(3)消元，可得

2x2-2x+z2-2z=0,

即

而正如文献[1]第148页所述：设空间曲线Γ的方程是

从中消去变数z，得到方程g(x,y)=0，它表示母线平行于z轴的柱面.

因此通过方程组(3)消元，得到的方程

因此，二元方程在二维空间表示平面图形，在三维空间中表示柱面.空间直角坐标系中表示平面图形只能用方程组表示.例如空间直角坐标系中，方程组

(4)

表示圆的方程.若将方程组(4)中消去y，则变成了椭圆柱面方程

而解法1巧妙地将平面ACC1A1作为坐标平面，使得柱面与坐标平面ACC1A1的交线就是圆，问题迎刃而解.

2 多维探究，拓展思维

笔者和学生一起探究几何法的解题思路.

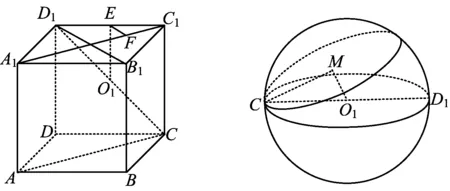
图4 图5

如图5所示，球O1的半径为

而O1M⊥⊙M，⊙M⊆面AA1C1C，因此O1M即为点O1到面AA1C1C的距离.

如图4所示，过点O1作O1E∥CC1交棱C1D1于点E，过点E作EF∥B1D1交A1C1于点F.由此可知，EF⊥面AA1C1C，故点O1到面AA1C1C的距离为

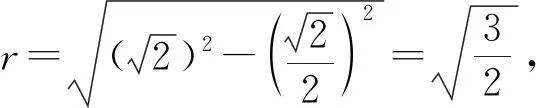
几何法是解决立体几何中动点问题的常见方法.求解例1的关键是作出点P的轨迹圆，而此圆是以CD1为直径的球面被平面ACC1A1所截形成的⊙M，因此为了更形象地观察点P的轨迹圆的特征，就必须将⊙M从正方体ABCD-A1B1C1D1中分离出来，以CD1为直径的球面为载体来呈现，进而构造直角三角形求解，如图5所示.

图6 图7

解法4(特殊点)如图7所示，因为D1H⊥面AA1C1C，且点P是平面ACC1A1上一动点，所以

D1H⊥CP.

即

D1P⊥CP，

从而

CP⊥面D1HP，

可知

CP⊥PH.

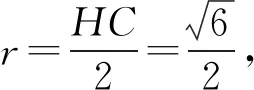
3 几点思考

3.1 强化问题探究意识

立体几何中动点的定量计算问题侧重于考查学生的直观想象能力、逻辑推理和数学运算能力，一般难度较大，在高考中也涉及不多.但是高考绝不是数学教育的终点，更重要的是数学教育承载着落实立德树人的根本任务、发展素养素质教育的功能.在教学实践中，我们不应该回避生1解法中出现的问题，更不能简单地否定.相反，我们应该抓住这一契机，顺势而为，引导学生剖析错误的根源，确定问题的症结，找到问题解决的办法，帮助学生走出困境[2].学生实现从平面解析几何的认知类比探究空间解析几何的跨越，为探索空间解析几何打开一扇门，在解决数学问题中完备知识体系，提升数学核心能力.这必将点燃学生心中那盏创新意识的火种，让探究活动成为学生的乐趣.这也正是新课程理念所倡导的以学生的发展为本，培育科学精神和创新意识，提升学生的核心素养[3].

3.2 落实传统几何法

几何法和坐标法是解决立体几何的两大法宝.但在立体几何问题中传统几何法对学生的视图能力、作图能力、空间想象能力以及逻辑推理能力较坐标法有较高的要求，因此在教学中，我们发现学生会逃避几何法，导致简单立体几何问题出现“套路”解题的现象.例如，球体被平面所截的几何图形一定是圆，求圆的面积，就是求圆的半径，问题转化为如何直观地作出圆或者找到圆的内接直角三角形，这是关键.这需要教师引领学生在画图、识图中对具体图形的位置关系、度量关系由直观感知、操作确认上升到理性认知的过程，从中发现图形的本质特征.总之，在立体几何中构建空间观念、培养学生的直观想象素养势在必行.